In a n×n Latin square, each of the numbers 1 through n appears exactly once in each row and column. For example, the 5 × 5 square below is a Latin square.
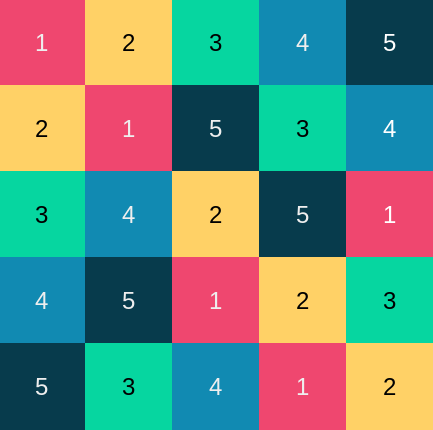
If we placed a rook on each square numbered 1, the rooks would not attack each other since no two rooks would be in the same row or the same column. The same would be true if we moved all the rooks to squares numbered 2, or 3, etc.
Now imagine a n×n×n chess cube, a stack of n chessboards, each board being n×n. For example, we could have a stack of eight standard 8×8 boards.
In our 3D chess cube, rooks can move any number of squares in either the x or y direction within a board, and they can also move vertically in the z direction.
Put a rook on every square of the bottom board. Then take the rooks on squares numbered 2 and move them to the second level. Take the rooks on squares numbered 3 and move them to the third level, and so forth.
Now we have n×n rooks, and none is in a position to attack the other. To see this, pick a particular level k. None of the rooks on level k are attacking each other because level k is a Latin square. And none of the rooks can attack vertically because we started with all the rooks on the bottom level and lifted them up by various amounts; there’s only one rook in each vertical column.
Next let’s suppose we have n×n rooks arranged in 3D so that none is attacking any of the others. Label the rooks on level k with a k. Now push all the rooks straight down vertically to the first level. There can only be one rook on each square because no rooks were attacking each other vertically.
Number each square by the number of its rook. I claim the result is a Latin square. There can only be one k in each row and column because all the ks started out on level k, and none were attacking each other in the x or y direction.

This is one of my favorite latin squares to use in an introductory class in abstract algebra. If we interpret the square as the multiplication table of a loop (quasigroup with identity element), the upper left corner indicates that 2*2 = 1. But the loop itself has order 5. Thus Lagrange’s Theorem is not satisfied, so this cannot possibly be the multiplication table of a group.