This post expands on a small part of the post Demystifying the Analemma by M. Tirado.
Apparent solar declination given δ by
δ = sin-1( sin(ε) sin(θ) )
where ε is axial tilt and θ is the angular position of a planet. See Tirado’s post for details. Here I want to unpack a couple things from the post. One is that that declination is approximately
δ = ε sin(θ),
the approximation being particular good for small ε. The other is that the more precise equation approaches a triangular wave as ε approaches a right angle.
Let’s start out with ε = 23.4° because that is the axial tilt of the Earth. The approximation above is a variation on the approximation
sin φ ≈ φ
for small φ when φ is measured in radians. More on that here.
An angle of 23.4° is 0.4084 radians. This is not particularly small, and yet the approximation above works well. The approximation above amounts to approximating sin-1(x) with x, and Taylor’s theorem tells the the error is about x³/6, which for x = sin(ε) is about 0.01. You can’t see the difference between the exact and approximate equations from looking at their graphs; the plot lines lie on top of each other.
Even for a much larger declination of 60° = 1.047 radians, the two curves are fairly close together. The approximation, in blue, slightly overestimates the exact value, in gold.
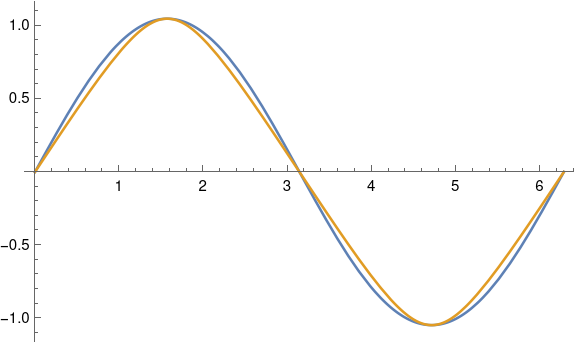
This plot was produced in Mathematica with
ε = 60 Degree
Plot[{ε Sin[θ] ], ArcSin[Sin[ε] Sin[θ]]}, {θ, 0, 2π}]
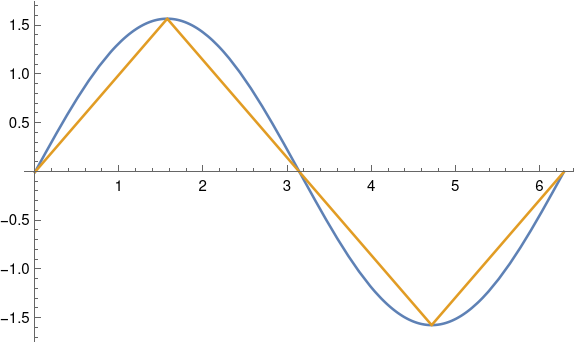
As ε gets larger, the curves start to separate. When ε = 90° the gold curve becomes exactly a triangular wave.
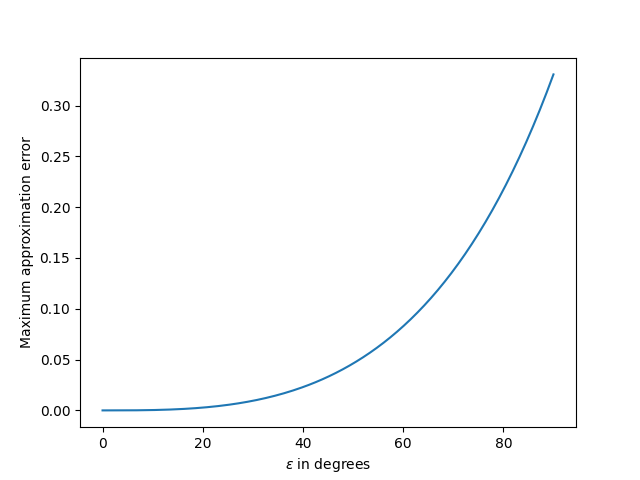
Update: Here’s a plot of the maximum approximation error as a function of ε.