How flat is a normal mixture on top?

Posted on by John

Male and female heights both have a standard deviation of about 3 inches, with means of 70 inches and 64 inches. That’s a good first-pass model using round numbers.

If you ask what the height of an average adult is, not specifying male or female, you get a mixture of two normal distributions. If we assume an equal probability of selecting a male or female, then the probability density function for the mixture is the average of the density functions for men and women separately.

This mixture distribution is remarkably flat on top.

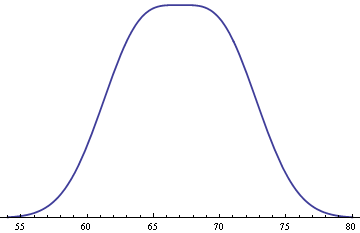
This happens whenever you have an equal mixture of two normal distributions, both having the same standard deviation σ, and with means 2σ apart. If the means were any closer together, the distribution would be rounder on top. If the means were any further apart, there would be a dip in the middle.

This makes sense intuitively if you think about what happens if you make things more extreme. If the means were as close together as possible, i.e. if they were the same, we’d simply have a normal distribution with its familiar curve on top. If the means were much further apart, we’d have two bumps that hardly appear to overlap.

See more on the application to heights here.

Mathematical details

How flat is the mixture density on top? We can quantify the flatness by looking at a power series expansion centered at the peak.

To simplify matters, we can assume that σ = 1 and that the means of the two distributions are -μ and μ, with the primary interest being the case μ = 1. The probability density function for the mixture is

\frac{1}{2\sqrt{2\pi}}\left( \exp\left(\frac{-(x-\mu)^2}{2} \right ) + \exp\left(\frac{-(x+\mu)^2}{2} \right )\right )

If we expand this in a Taylor series around 0 we get

\exp\left( -\frac{\mu^2}{2} \right) \left( \frac{1}{2 \pi }+\frac{\left(\mu^2-1\right) x^2}{4 \pi }+\frac{ \left(\mu^4-6 \mu^2+3\right) x^4}{48 \pi } + \cdots \right)

This is a little complicated, but it explains a lot. Notice that the coefficient of x² has a term (μ² – 1).

We said above that if the means were any closer together than two standard deviations, the distribution would be rounder on top. That’s because if μ < 1 then (μ² – 1) is negative and the curve is convex on top.

We also said that if the means were any further apart, there would be a dip in the middle. That’s because if μ > 1 then (μ² – 1) is positive and the curve is concave on top.

Now if μ = 1 then the x² term disappears. And because our function is even, its Taylor series only has terms with even powers. So if the x² term goes away the next term is not x3 but x4.

So one way to say how flat our curve is on top is that it is flat to within O(x4).

Let’s get more specific by evaluating the coefficients numerically. For small x, our mixture density function is

0.0965 – 0.0080 x4 + O(x6).

Now if x is small, x4 is extremely small, and the coefficient of 0.008 makes it even smaller.

4 thoughts on “How flat is a normal mixture on top?”

  1. Jonathan

    This reminds me of a question I was once curious about: are there any good statistical tests to distinguish between a sample being drawn from a single normal vs a mixed normal? I didn’t really research it much, but a reader here might know.

  2. Tomas

    Jonathan – the “machine learning answer” would be to fit the candidate distributions to the data and compare the likelihood of the data. You do want to have some reasonable prior on each class of distribution (number of mixture components).

  3. Andrew

    Another reason why this makes sense: a normal curve’s inflection points are at +/- sigma. So the second derivative of the mixture distribution at 0 will be 0 if the separation is sigma.

Comments are closed.