Draw a line in the complex plane. What is the image of that line when you apply the exponential function?
A line through w with direction z is the set of points w + tz where w and z are complex and t ranges over the real numbers. The image of this line is
exp(w+ tz) = exp(w) exp(tz)
and we can see from this that character of the image mostly depends on z. We can first plot exp(tz) then rotate and stretch or shrink the result by multiplying by exp(w).
If z is real, so the line is horizontal, then the image of the line is a straight line.
If z is purely imaginary, so the line is vertical, then the image of the line is a circle.
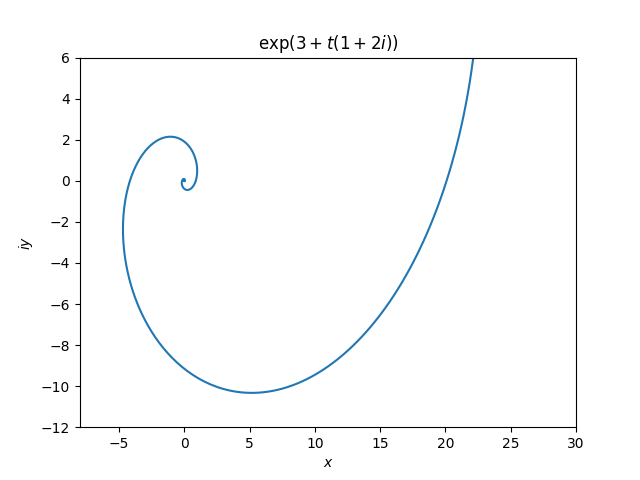
But for a general value of z, corresponding to neither a perfectly horizontal nor perfectly vertical line, the image is a spiral.
Since the imaginary part of z is not zero, the image curves. And since the real part of z is not zero, the image spirals into the origin, either as t goes to infinity or to negative infinity, depending on the sign of the real part of z.
Here’s an example, the image of the line through (3, 0) with slope 2.