The previous post gave the details of how Möbius transformations
m(z) = (az + b)/(cz + d)
transform circles. The image of a circle under a Möbius transformation is either a line or a circle, and in our examples the image will always be a circle.
We start with an approximation of the Olympic rings
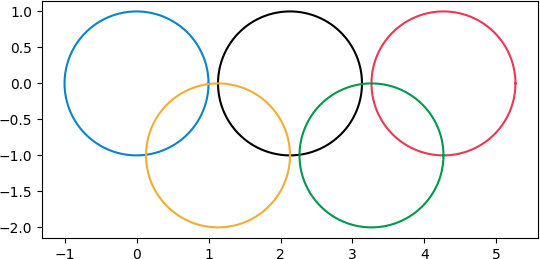
and then apply various transformations.
First we apply (z + 9)/(z + 10):
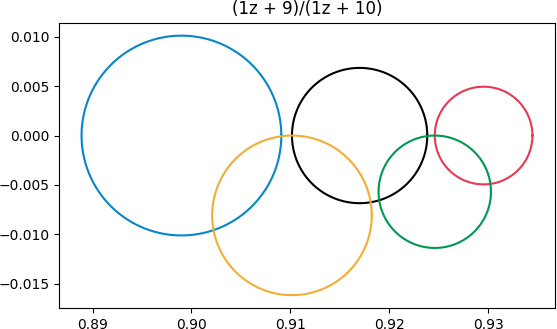
This transformation doesn’t distort the rings too much because the rings are far from the singularity at z = -10. The blue ring is distorted the most because it’s closest to the singularity.
Next we apply (iz + 7)/(z + 8). Now we’ve moved the singularity a little bit closer, and we caused some rotation by using i as the coefficient of z in the numerator.
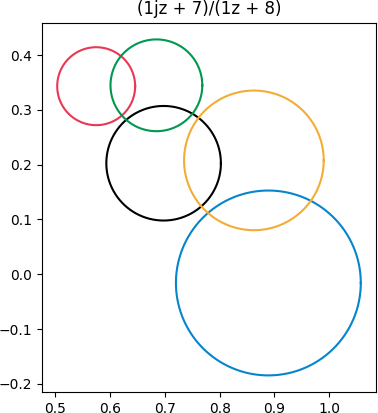
Finally, let’s pick a transformation with its singularity inside the green circle, (z + 4)/(z -3 + i).
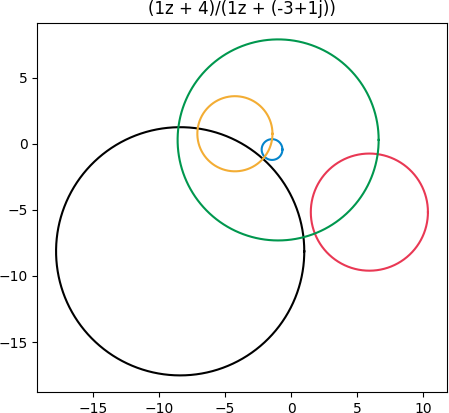
Now we see a lot of distortion. The blue and gold rings that were outside the green ring are brought inside. The complex plane is turned inside-out because of the singularity.
As before, the black and red rings still intersect the green ring. But what you can’t tell from the graph is that the portion of these rings that was inside has been turned outside and vice versa.

First and last sentence confused me.
1st the images are circles throughout, so “line” is propably a typo.
But why can’t we see in the last example where the in/outside of the red and black circles go? Some elementary topology suffices: The circles from the outside stay outside…
I fixed the typo at the top. Thanks.
To understand the last part, imagine our transformation is 1/z and the green circle is the unit circle. If |w| < 1, then |1/w| > 1. Everything originally outside the unit circle comes in, and everything originally inside the unit circle goes out.
I believe the post just means that, say, if you just looked at the red and green circles in the original and in the final, it’s not clear that the “inside” went to the “outside” and vice-versa (whereas this is quite clear for the blue and yellow rings, vis-a-vis the green)
Topology only: Möbius transforms are isomorphisms of the (Riemann) sphere. 2 non intersecting circles topologically divide the sphere into say the arctic and antarctic caps and an aequatorial belt. The singularity is where we remove a point from the sphere. Puncturing the belt gives us two disjoint circles both outside each other. Puncturing the arctic cap gives us the antarctic circle inside the arctic one. So in this situation topology suffices to tell in which of the 3 areas the singularity resides. Astonishingly in case of 2 intersecting circles topology does not help distinguishing the 4 possibilities.
Boom! Interesting stuff I’ll! I’ll add that to my 3 ring binder…