Direction between two cities

This post is the third in a series of posts on spherical trigonometry. We first looked at the analog of the Pythagorean theorem on a sphere, then the analog of the law of cosines on a sphere. Now we look at the analog of the law of sines on a sphere.

As before we denote the sides of a triangle with a, b, and c and denote the angle opposite a side by the capital version of that letter. So A is the angle opposite side a and so forth.

The law of sines on a sphere says

sin a / sin A = sin b / sin B = sin c / sin C.

Small triangles

Suppose for a moment that we’re looking at a relatively small triangle, one for which the length of the sides is small relative to the radius of the sphere. Then we can apply the small angle approximation

sin x ≈ x

to each side [1] and find

a / sin A ≈ b / sin B ≈ c / sin C.

In other words, the law of sines from plane trigonometry holds approximately in spherical trigonometry for small triangles. This is not surprising since we know we can ignore the curvature of the earth when working over relatively small areas, but it is reassuring.

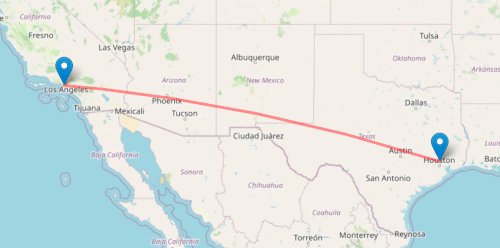
Example: LAX to IAH

In the previous post we found the air distance between LAX (Los Angeles) and IAH (Houston) airports by making a spherical triangle with vertices at LAX, IAH, and the north pole. We labeled the side from LAX to the north pole a and the side from IAH to the north pole b. We found the length of side c using the law of cosines.

Now suppose we’re at LAX and about to fly to IAH. What direction should we fly? Since Los Angeles and Houston are approximately at the same latitude, and they’re not terribly far apart relative to the size of the earth, we know that we’ll roughly fly due east. Let’s find the flight direction more precisely.

The angle B in our triangle gives us the angle between our heading and a heading of due north. We know b from the latitude of IAH, we know C from the difference in longitude of the two airports, and we found c in the previous post. Therefore we can find B from the law of sines:

sin b / sin B = sin c / sin C

and we know everything but B. So

sin B = sin b sin C / sin c = sin 60.02° sin 23.07° / sin 19.92°.

This tells us sin B = 0.9960. So what is B? If we ask software for the arcsine of 0.9960 we will get 84.88°. This would say we head 5.12° north of due east to get from Los Angeles to Houston. But Houston is at a lower latitude than Los Angeles and so that doesn’t seem right.

In the first post in this series I mentioned that a flight between Houston and Wuhan would fly over Alaska even though the two cities are at essentially the same latitude. Wuhan is at a slightly higher latitude than Houston, but a flight leaving Wuhan for Houston would head somewhat north. So it is possible that a flight from a higher latitude to a lower latitude would head north [2].

But Los Angeles is much closer to Houston than Wuhan is, and the difference in latitude is greater. A flight from LA to Houston would head mostly east and a little south. So where did we go wrong?

The arcsine function in any software package returns a solution to the equation

sin(x) = y,

but it might not return the solution we need. The angle 84.88° is a valid solution to the equation

sin(B) = 0.9960

but it’s not the appropriate solution in our context. We need the solution 95.12°. Our flight heada 5.12° south of east. This assumes our flight takes a great circle path; airlines may have reasons not to take the shortest possible path between two airports.

***

[1] The approximation assumes x is measured in radians. If we measure angles in degrees or any other units, the right side of the approximation will need to be multiplied by a constant. But the same constant will appear in all the numerators and denominators of the law of sines and so the approximation holds in any units.

[2] Here’s another illustration of the same point. Draw a circle around the north pole, say a circle a mile in diameter, and suppose you want to walk from longitude 0 to longitude 180°. Following a path of constant latitude is walking around the circle. Heading north instead is walking across the diameter of the circle. If your destination is a little bit outside the circle on the other side, it’s still shorter to walk across the circle, i.e. head north, even though your destination is at a lower latitude, i.e. south.