How does the circumference of a circle vary with its radius? What about the area? The answers are simple and familiar in Euclidean geometry, but not as simple or as familiar in non-Euclidean geometry.
This post will look at how circumference and area vary as a function of radius in three spaces: a surface with constant curvature 1 (i.e. a unit sphere), a surface of constant curvature 0 (i.e. a plane), and a surface of constant curvature -1 (a hyperbolic surface). The radius in each case is the distance from the center to the circle as measured on the surface.
Spherical case
In the spherical case, a circle of radius r has circumference
C(r) = 2π sin(r)
and area
A(r) = 2π (1 − cos(r)).
The circumference formula is valid for 0 ≤ r ≤ π and the area formula is valid for 0 ≤ r ≤ π/2.
Hyperbolic case
In the hyperbolic case, a circle of radius r has circumference
C(r) = 2π sinh(r)
and area
A(r) = 2π (cosh(r) − 1).
These formulas are valid for 0 ≤ r < ∞.
Plots
Let’s make a couple plots to illustrate the equations above. First, circumference as a function of radius.
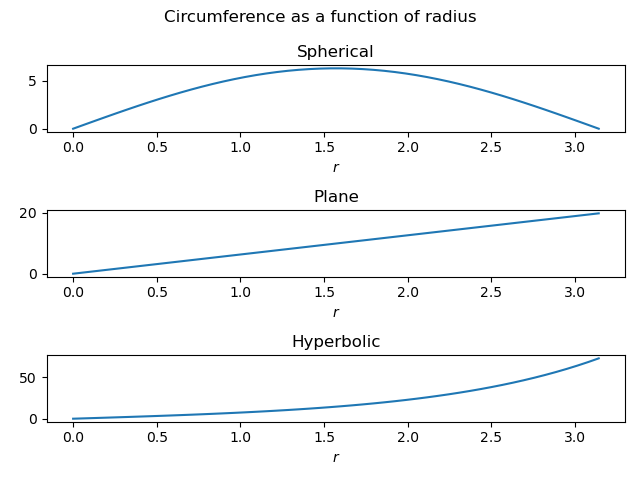
The top subplot looks surprising at first. Can circumference decrease when radius increases? Yes, on a sphere. Imagine a circle around the north pole. As we pull that circle down from the pole, the circumference increases until the circle becomes the equator. Past that point, the circumference of the circle decreases as the circle descends further south.
Using the same range of r for all three subplots obscures the fact that the circumference of a circle in the hyperbolic case grows exponentially with the radius.
Next let’s look at area as a function of radius.
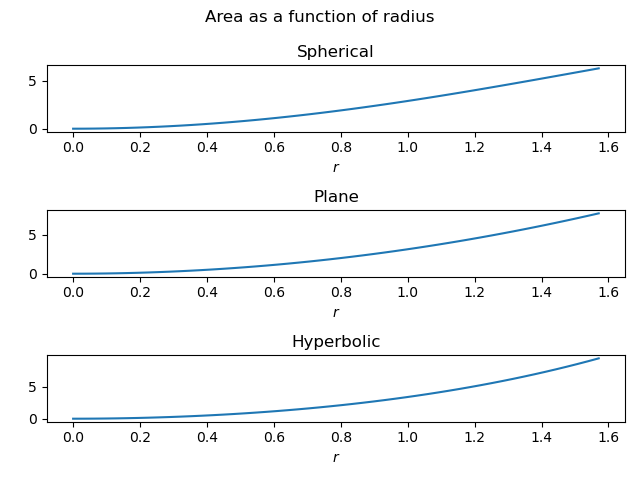
In each case, area grows approximately quadratically with radius. But again the growth in the hyperbolic case is exponential as r increases further than is possible in the spherical case.
One last note: In the plane, the ratio of area to circumference is proportional to r. In the hyperbolic case, the same ratio is asymptotically constant, independent of r.
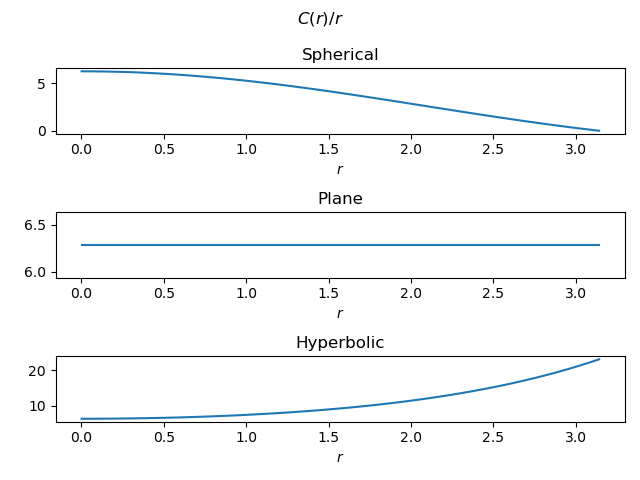
Update
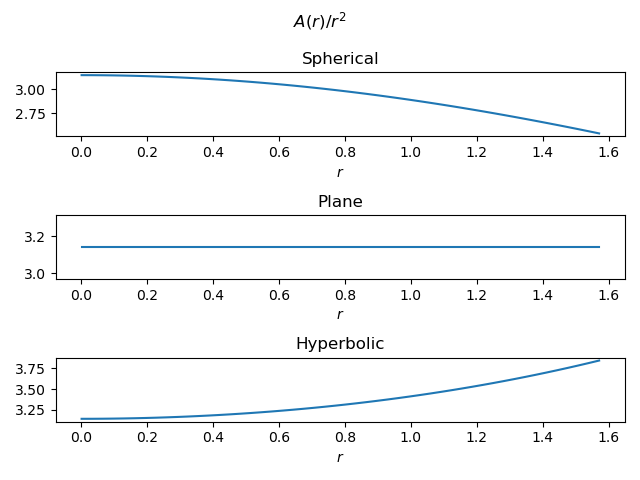
Here’s a plot of C(r) / r.
And here’s a plot of A(r) / r².