The most common way to define an ellipse geometrically is as the set of points whose distances to two foci sum to a constant. There is another way, however, to define an ellipse that generalizes to include the two other conic sections, parabolas and hyperbolas.
You can define a conic section as the set of points whose distance to a focus equals a constant multiple of the distance to a line called the directrix. This multiple is denoted e for eccentricity. If 0 < e < 1 you get an ellipse. If e = 1 you get a parabola, and if e > 1 you get a hyperbola [1].
The previous post defined the latus rectum for an ellipse. More generally, the latus rectum is the chord through the focus and parallel to the directrix.
And with this definition, you can define the latus rectum for each of the conic sections.
Ellipse
Given an ellipse with equation
x²/a² + y²/b² = 1
where a > b, the foci are at ± c where c = √(a² – b²). The eccentricity is e = c/a.
Consider the focus at –c. If the directrix is the line x = –d then the distance from the focus (-c, 0) to left vertex of the ellipse at (-a, 0) equals e times the distance from (-a, 0) to the point (-d, 0) on the directrix, and so
a – c = (c/a)(d – a)
and we find d = a²/c.
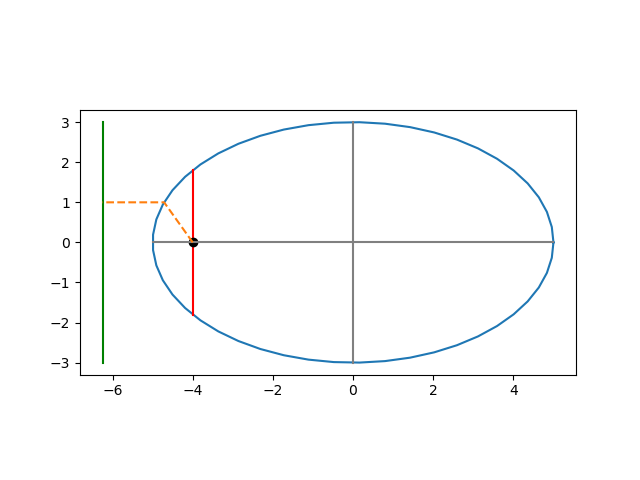
In the plot below, the green vertical line to the left of the ellipse is the directrix. The red vertical line through the focus is the latus rectum. The length of the orange segment from the focus to the ellipse should be e times the length of the segment from the point on the ellipse to the directrix.
Parabola
For a parabola with equation
y² = 4ax
with a > 0, the focus is at (a, 0) and the directrix is the line x = –a. The eccentricity of a parabola is 1.
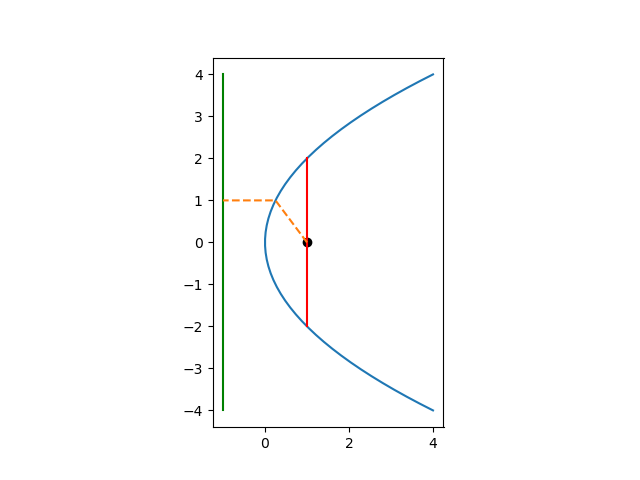
Here again the green vertical line to the left of the parabola is the directrix and the red vertical line through the focus is the latus rectum. The two dashed orange lines have the same length.
Hyperbola
Given a hyperbola with equation
x²/a² – y²/b² = 1
where a > b, the foci are at ± ae where the eccentricity is e = √(1 + b² / a²).
Let d = a²/c. Then either the line x = d or the line x = –d could be used as the directrix.
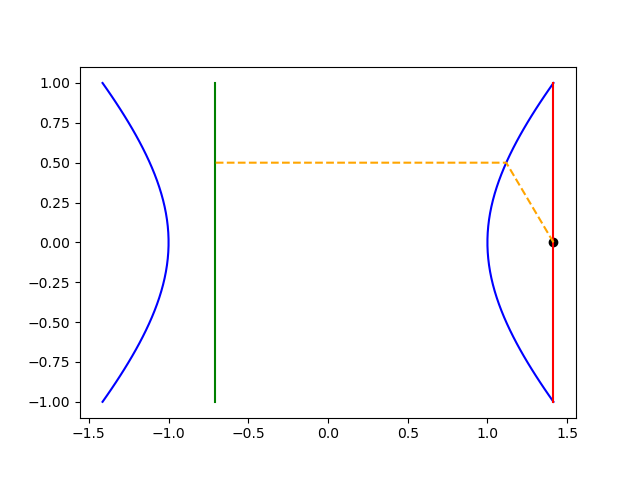
As before the green vertical line is the directrix and the red vertical line through the focus is the latus rectum. The lengths of the two dashed orange lines are proportional, and the proportionality constant is the eccentricity e.
Related posts
- Latus rectum of an ellipse
- Best approximation of a catenary by a parabola
- Trig in hyperbolic geometry
[1] The case e = 0 gives a circle, but now the definition doesn’t apply directly. The circle is the limit as e goes to 0 and the directrix moves further and further away. Projective geometry gives a way to rigorously say the directrix is a line at infinity without taking limits.
