Ellipses have been studied for over two thousand years, and so some of the terminology is ancient and sounds odd to modern ears. One such term is latus rectum. What is the latus rectum and does have it anything to do with anatomy?
This post defines the latus rectum for an ellipse. See the next post for a more general definition that extends to parabolas and hyperbolas.
Background
An ellipse has two foci, two points such that the distance to one plus the distance to the other remains constant for every point on the ellipse. For a circle, the two foci coincide with the center.
Given an ellipse in the plane, we can pick a coordinate system so that our ellipse has equation
x²/a² + y²/b² = 1
where a ≥ b > 0. Here a is called the semi-major axis and b the semi-minor axis. The two foci are located at ±c where
c² = a² − b².
The ratio c/a is the eccentricity. As discussed here, eccentricity can be moderately large and yet the ellipse still be close to a circle.
Definition
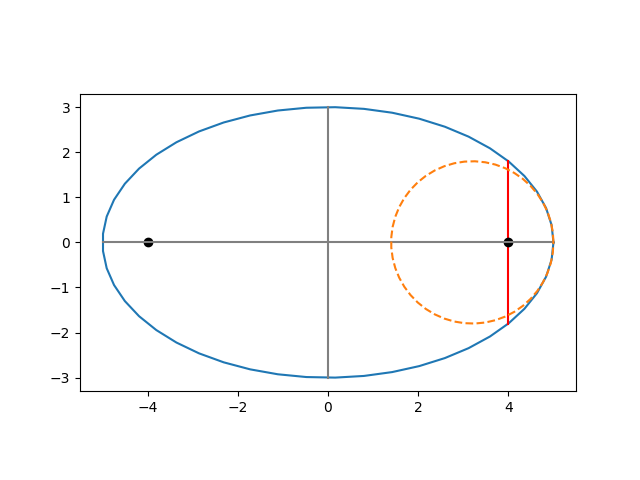
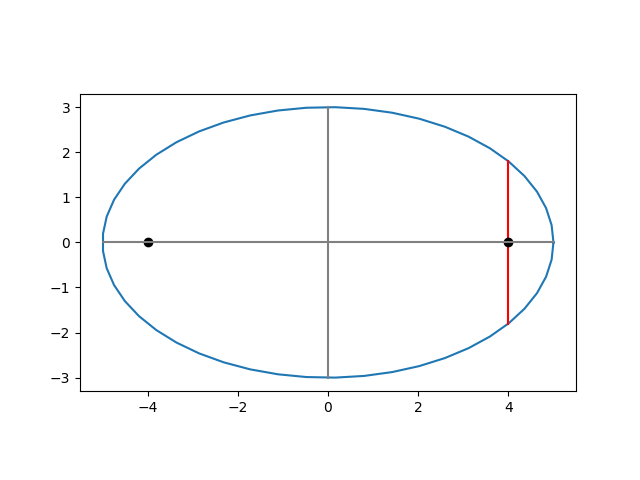
Pick one of the foci, say the one located at (c, 0). Then the line segment through the focus, parallel to the minor axis and connecting two points on the ellipse, is called the latus rectum. Its length is 2b² / a.
Example
Let the semi-major axis be a = 5 and the semi-minor axis be b = 3. Then c = 4 and so the foci are located at (-4, 0) and (4, 0).
When x = 4, the equation of the ellipse tells us
16/25 + y²/9 = 1
and so y = ±9/5. So the latus rectum is the line connecting (4, −9/5) and (4, 9/5), the red vertical line below.
Why the name?
The first part latus mean side and the second part rectum means straight. According to Etymonline, rectum was
the name given to the lowest part of the large intestine by Galen, who so called it because he dissected only animals whose rectum (in contradistinction to that of man) is really straight.
So latus rectum means straight side. If you wanted to draw straight sides on an ellipse, where would you put them? Through the foci seems like as good a choice as any.
Radius of curvature
An interesting fact about the latus rectum is that its length is the diameter of a kissing circle tangent to the vertex of the ellipse. In other words, the semi-latus rectum, half the length of the latus rectum, is the radius of curvature at the vertex.
The dashed orange circle below has radius 9/5, equal to the semi-latus rectum. So the radius of curvature at the right end of the ellipse is 9/5 and the curvature is 5/9.