I wrote last week that the eccentricities of planet orbits in our solar system do not effect the shape of the orbit very much. Here’s a plot of all the orbits, shifted to have the same center and scaled to have the same minor axis.

However, the planet orbits do not have a common center. The eccentricity of an orbit doesn’t affect its shape as much as its position. Eccentric orbits are off-center. That’s literally what eccentric means.
Kepler’s laws say that each planet orbits in an ellipse with the sun at one focus of that ellipse. That means the more eccentric an orbit is, the further the center of the orbit is from the sun.
If a planetary orbit has semi-major axis a and the foci are a distance c from the center, then the eccentricity e equals c/a. If we scale all the planetary orbits so that they each have a semi-major axis equal to 1, then e = c, i.e. the eccentricity equals the distance from each focus to the center.
Imagine the sun as the center of our coordinate system and that each planet’s orbit is aligned so that its major axis is along the x axis. Each orbit has the sun, i.e. the origin, as a focus, and so the center of each orbit is at –e where e is the eccentricity of that orbit. Here’s the plot above redone to fix the sun rather than to fix the center. The black dot in the center is the sun.

Here is the same plot with only Venus and Pluto.
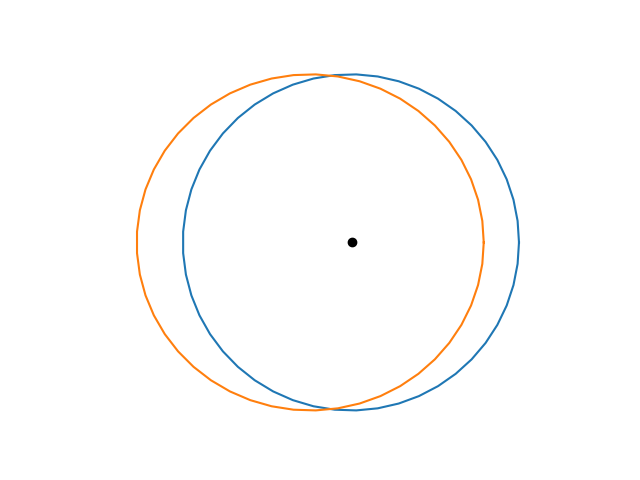
The orbit of Venus is essentially a circle centered at the sun. The orbit of Pluto is an ellipse with major axis about 3% longer than its minor axis. It’s hard to see that the shape of Pluto’s orbit is not a circle, but it’s easy to see that the orbit is off-center, i.e. eccentric.
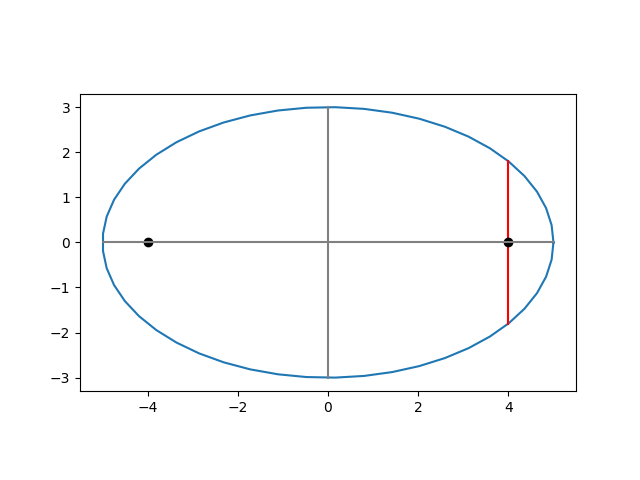
This post explains why moderately large eccentricities do not have much impact on the aspect ratio of an ellipse.
The image below from this post shows an ellipse with eccentricity 0.8. The two foci are far from the center, and yet the the aspect ratio is 3 : 5. It’s obviously an ellipse, but the foci are further apart than you might imagine.