Elliptical orbit example: Mars Orbiter Mission

This post will look at India’s first interplanetary mission, Mars Orbiter Mission, to illustrate points in recent posts.

As suggested by the logo, the probe had a very eccentric orbit of Mars with periareion 3,812 km and apoareion 80,384 km. We can derive everything else from these numbers. [1]

Peri-what?! As mentioned in footnote 2 of this post the nearest and furthest points of a satellite’s orbit go by various names depending on what the satellite is orbiting. The terms perigee and apogee for Earth satellites are more familiar; the terms periareion and apoareion are the Martian counterparts. The names for the closest and furthest approaches of satellites of Jupiter would be perijove and apojove. The “areion” suffix refers to Ares, the Greek name for Mars.

So the Mars Orbiter Mission (MOM) was much closer to Mars on its nearest approach than on the opposite side of its orbit, 21 times closer. That means its tangential velocity was 21 times faster at periareion than at apoareion [2].

The orbit was an ellipse with major axis 3,812 km + 80,384 km = 84,196 km. The semi-major axis was a = 42,098 km. The center of Mars was a distance c = a – 3,812 km = 38,286 km from the center. The eccentricity was thus e = c/a = 0.909.

Using the equations from this post we find that the aspect ratio of the ellipse was 0.4158.

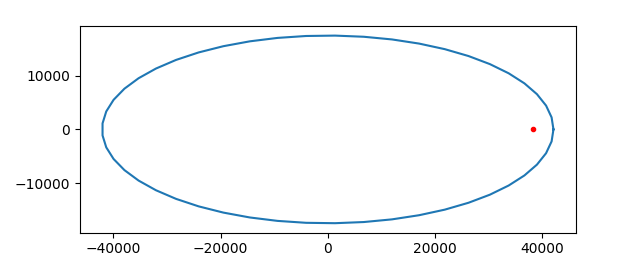
Although the deviation of the orbit from circular is substantial, the distance of Mars from the center of the orbit is dramatic. More on this here.

Using the formulas from this post we can plot the mean anomaly, true anomaly, and eccentric anomaly for MOM.

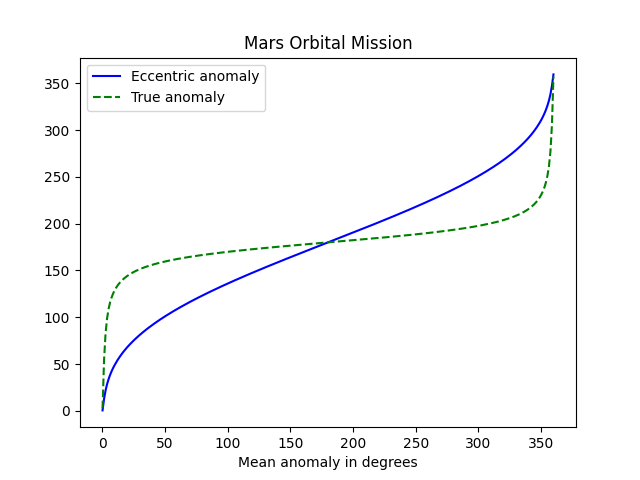
The steep lines on the far left and far right show how quickly the probe is moving at nearest approach to the planet. The true anomaly is the angle to the satellite based at Mars, and this angle changes very rapidly when the probe is near the planet. Eccentric anomaly is measured from the center of the orbit and so it does not change as quickly.

The period along with either the true anomaly or eccentric anomaly is enough to know the position of the satellite at all times. We can determine the period of a satellite from Kepler’s laws:

T = 2π √(a³/μ)

where μ = GM, with G being the gravitational constant and M being the mass of Mars. Now G = 6.674 × 10⁻¹¹ N m²/kg² and M = 6.417 × 10²³ kg. We’ll need to multiply a by 1,000 to work in units of meters. This gives us a period of 262,242 seconds or about 73 hours.

***

[1] My understanding is that while perigee and apogee are measured as altitude from the Earth’s surface, peri[planet] and apo[planet] are conventionally measured from the center of the planet for other planets. That’s how I’m using the terms here. When I first wrote this post, I used a value of periapeion from Wikipedia which was less than the radius of Mars and hence impossible. In retrospect the Wikipedia article was reporting an altitude.

[2] For objects in elliptical orbits, v_peri / v_apo = r_apo / r_peri. This follows from Kepler’s law that the vector from a planet to its satellite sweeps out equal area in equal time.