Pascal’s triangle mod row number

Almost all binomial coefficients are divisible by their row number.

This is a theorem from [1]. What does it mean?

If you iterate through Pascal’s triangle, left-to-right and top-to-bottom, noting which entries C(m, k) are divisible by m, the proportion approaches 1 in the limit.

The author proves that the ratio converges to 1, but doesn’t say anything about the rate at which it approaches 1. By writing a little Python script we can observe how the ratio approaches 1.

First, let’s create a generator that will let us walk through Pascal’s triangle.

    def pascal():
        m, k = 0, 0
        while True:
            yield (m, k)
            k += 1
            if k > m:
                m += 1
                k = 0

We can use this generator to illustrate Pascal’s triangle mod row number.

    from math import comb

    p = pascal()
    m, k = next(p)
    while m < 10:
        ch = "*"
        if m > 0 and comb(m, k) % m == 0:
            ch = "0"
        print(ch, end="")
        if m == k:
            print()
        m, k = next(p)

This produces the following.

    *
    00
    *0*
    *00*
    *0*0*
    *0000*
    *0***0*
    *000000*
    *0*0*0*0*
    *00*00*00*

The theorem says that as we keep going, the proportion of 0’s in a diagram like the one above approaches 1.

Now let’s plot the proportion of zeros as we traverse Pascal’s triangle mod row number.

    N = 1000
    x = np.zeros(N)
    p = pascal()
    for n in range(N):
        m, k = next(p)
        if m > 0 and comb(m, k) % m == 0:
            x[n] = 1
    y = np.arange(N)
    plt.plot(y, x.cumsum()/y)
    plt.show()

Here’s what we get.

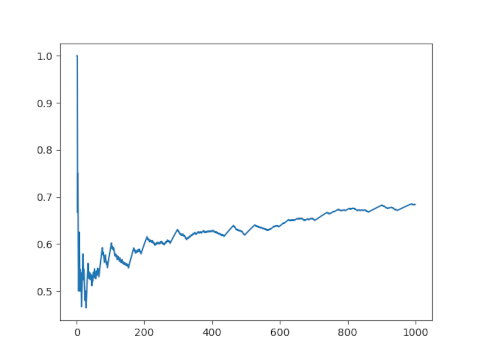
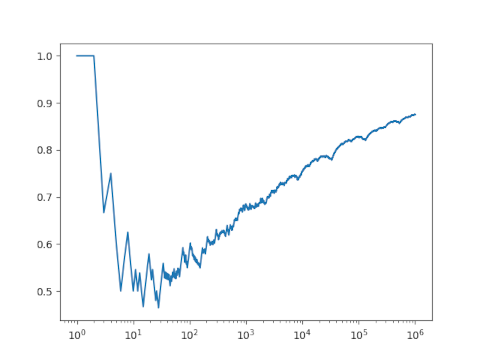
The ratio doesn’t seem to be converging to 1. If I had to guess, I might say it’s converging to 0.7 by looking at this plot. But if we go further out and switch to a log scale it seems more plausible that the sequence is converging to 1, albeit very slowly.

[1] Heiko Harborth. Divisibility of Binomial Coefficients by Their Row Number. The American Mathematical Monthly, Jan. 1977, Vol. 84, No. 1, pp. 35–37.