Van Aubel’s theorem is analogous to Napoleon’s theorem, though not a direct generalization of it.
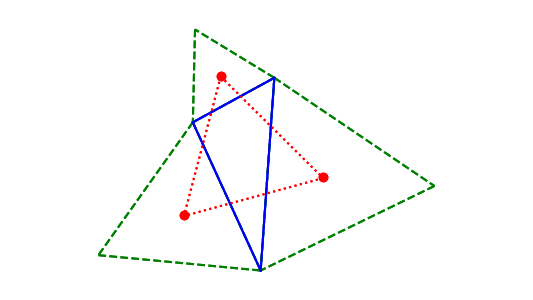
Napoleon’s theorem says to start with any triangle and draw equilateral triangles on each side. Connect the centers of the three new triangles, and you get an equilateral triangle.
Now suppose you start with a quadrilateral and draw squares on each side. Connect the centers of the squares. Do you get a square? No, but you do get something interesting.
Van Aubel’s theorem says that if you connect the centers of squares on opposite faces of the quadrilateral (dashed lines below), the two line segments are the same length and perpendicular to each other.
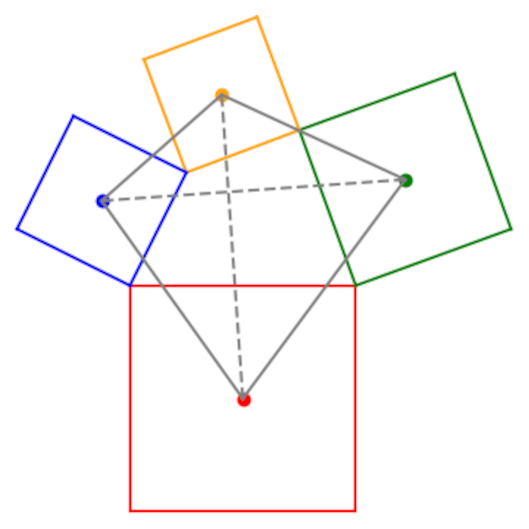
The solid gray lines show that if you connect the centers of the square you do not get a square.
Further development
Van Aubel’s theorem dates to 1878 [1], and there have been numerous extensions ever since. Recently [2] Pellegrinetti found that six points related to Van Aubel’s theorem all lie on a circle. The six points are the midpoints of the two Van Aubel line segments (the dashed line segments above), the intersection of these two line segments, the midpoints of the two diagonals of the quadrilateral, and one more point.
The final point in Pellegrinetti’s theorem comes from flipping each of the squares over, connecting the centers, and noting where the connecting lines intersect. This is analogous to the messy case of Napoleon’s theorem: When you draw the squares on the inside of the quadrilateral rather than on the outside, the picture is hard to take in.
There are variations on Van Aubel’s theorem that generalize squares to rectangles, rhombi, and parallelograms. [3]
[1] Van Aubel, H., Note concernant les centres des carrés construits sur les cotés dun polygon quelconque, Nouv. Corresp. Math., 4 (1878), pp. 40–44.
[2] Dario Pellegrinetti. The Six-Point Circle for the Quadrangle. International Journal of Geometry. 4 (2019) No 2, pp. 5–13.
[3] Michael de Villiers. Generalizing Van Aubel Using Duality. Mathematics Magazine. Vol. 73, No. 4, October 2000. pp. 303–307
