“The only use I know for a confidence interval is to have confidence in it.” — L. J. Savage
Can you have confidence in a confidence interval? In practice, yes. In theory, no.
If you have a 95% confidence interval for a parameter θ, can you be 95% sure that θ is in that interval? Sorta.
Frequentist theory
According to frequentist theory, parameters such as θ are fixed constants, though unknown. Probability statements about θ are forbidden. Here’s an interval I. What is the probability that θ is in I? Well, it’s 1 if θ is in the interval and 0 if it is not.
In theory, the probability associated with a confidence interval says something about the process used to create the interval, not about the parameter being estimated. Our θ is an immovable rock. Confidence intervals come and go, some containing θ and others not, but we cannot make probability statements about θ because θ is not a random variable.
Here’s an example of a perfectly valid and perfectly useless way to construct a 95% confidence interval. Take an icosahedron, draw an X on one face, and leave the other faces unmarked. Roll this 20-sided die, and if the X comes up on top, return the empty interval. Otherwise return the entire real line.
The resulting interval, either ø or (-∞, ∞), is a 95% confidence interval. The interval is the result of a process which will contain the parameter θ 95% of the time.
Now suppose I give you the empty set as my confidence interval. What is the probability now that θ is in the empty interval? Zero. What if I give you the real line as my confidence interval. What is the probability that θ is in the interval? One. The probability is either zero or one, but in no case is it 0.95. The probability that a given interval produced this way contains θ is never 95%. But before I hand you a particular result, the probability that the interval will be one that contains θ is 0.95.
Bayesian theory
Confidence intervals are better in practice than the example above. And importantly, frequentist confidence intervals are usually approximately Bayesian credible intervals.
In Bayesian statistics you can make probability statements about parameters. Once again θ is some unknown parameter. How might we express our uncertainty about the value of θ? Probability! Frequentist statistics represents some forms of uncertainty by probability but not others. Bayesian statistics uses probability to model all forms of uncertainty.
Example
Suppose I want to know what percentage of artists are left handed and I survey 400 artists. I find that 127 of artists surveyed were southpaws. A 95% confidence interval, using the most common approach rather than the pathological approach above, is given by
This results in a confidence interval of (0.272, 0.363).
Now suppose we redo our analysis using a Bayesian approach. Say we start with a uniform prior on θ. Then the posterior distribution on θ will have a beta(128, 264) distribution.
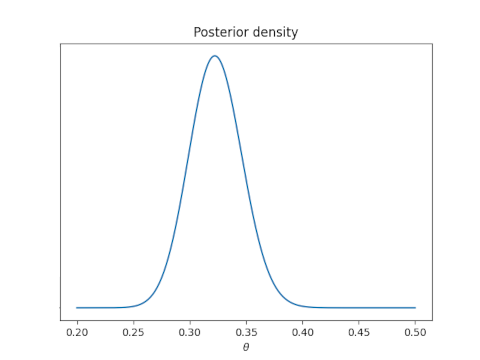
Now we can say in clear conscience that there is a 94% posterior probability that θ is in the interval (0.272, 0.363).
There are a couple predictable objections at this point. First, we didn’t get exactly 95%. No, we didn’t. But we got very close.
Second, the posterior probability depends on the prior probability. However, it doesn’t depend much on the prior. Suppose you said “I’m pretty sure most people are right handed, maybe 9 out of 10, so I’m going to start with a beta(1, 9) prior.” If so, you would compute the probability of θ being in the interval (0.272, 0.373) to be 0.948. Your a priori knowledge led you to have a little more confidence a posteriori.
Commentary
The way nearly everyone interprets a frequentist confidence interval is not justified by frequentist theory. And yet it can be justified by saying if you were to treat it as a Bayesian credible interval, you’d get nearly the same result.
You can often justify an informal understanding of frequentist statistics on Bayesian grounds. Note, however, that a Bayesian interpretation would not rescue the 95% confidence interval that returns either the empty set or the real line.
Often frequentist and Bayesian analyses reach approximately the same conclusions. A Bayesian can view frequentist techniques as convenient ways to produce approximately correct Bayesian results. And a frequentist can justify using a Bayesian procedure because the procedure has good frequentist properties.
There are times when frequentist and Bayesian results are incompatible, and in that case the Bayesian results typically make more sense in my opinion. But very often other considerations, such as model uncertainty, are much more substantial than the difference between a frequentist and Bayesian analysis.

I think that from the frequentist perspective, if it makes sense to say that θ is unknown but fixed, then it must also make sense to sat that I is known but random. Therefore it does make sense for a frequentist to say that there’s a 95% chance that θ is in some confidence interval I, but they mean something different than what a bayesian would understand by that.