I’ve mentioned the harmonic mean multiple times here, most recently last week. The harmonic mean pops up in many contexts.
The contraharmonic mean is a variation on the harmonic mean that comes up occasionally, though not as often as its better known sibling.
Definition
The contraharmonic mean of two positive numbers a and b is
and more generally, the contraharmonic mean of a sequence of positive numbers is the sum of their squares over their sum.
Why the name?
What is “contra” about the contraharmonic mean? The harmonic mean and contraharmonic mean have a sort of reciprocal relationship. The ratio
equals a/b when m is the harmonic mean and it equals b/a when m is the contraharmonic mean.
Geometric visualization
Construct a trapezoid with two vertical sides, one of length a and another of length b. The vertical slice through the intersection of the diagonals, the dashed blue line in the diagram below, has length equal to the harmonic mean of a and b.
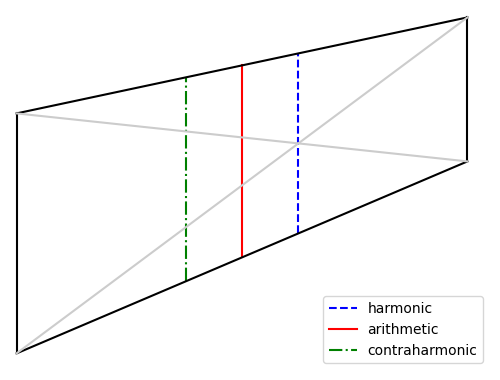
The vertical slice midway between the two vertical sides, the solid red line in the diagram, has length equal to the arithmetic mean of a and b.
The vertical slice on the opposite side of the red line, as from the red line on one side as the blue line is on the other, the dash-dot green line above, has length equal to the contraharmonic mean of a and b.
Connection to statistics
The contraharmonic mean of a list of numbers is the ratio of the sum of the squares to the sum. If we divide the numerator and denominator by the number of terms n we see this is the ratio of the second moment to the first moment, i.e. the mean of the squared values divided the mean of the values.
This smells like the ratio of variance to mean, known as the index of dispersion D, except variance is the second central moment rather than the second moment. The second moment equals variance plus the square of the mean, and so
and

Do you know any practical use cases for the contraharmonic mean? Somehow I’ve never seen it used, even though the harmonic mean is ubiquitous in my line of work.
I do find your geometric visualization quite interesting. I think it points to a connection between the harmonic mean and perspective projections / homographies. If an axis aligned equilateral with a vertical line through the middle is transformed with a homography that keeps the all vertical, the splitting vertical line of the resulting trapezoid is the harmonic mean of the vertical sides. Is there something analogous that happens for other homographies though? I’ll have to think that through in more detail.
(The following is so far as I know perfectly useless, but I think it’s pretty.)
One of your earlier blog posts asked: what if you do the arithmetic-geometric mean thing but instead use the arithmetic and harmonic means? Answer: you converge rapidly to the geometric mean. (Handwavy one-sentence proof: the product of the two values never changes.)
Well, what if you do the same with the contraharmonic and harmonic means? Answer: you converge rapidly to the _arithmetic_ mean. (Handwavy one-sentence proof: the sum of the two values never changes.)
One can invent other even more useless theorems of similar type. The “AHM” iteration preserves the GM and therefore converges to it. The “ChHM” iteration preserves the AM and therefore converges to it. Can we find a similar iteration that preserves the HM? Yes, of course: just take the reciprocal of everything. So if we do an AGM-like process where the two means are the arithmetic mean and the thing that takes a,b to ab(a+b)/(a^2+b^2), then it converges to the HM of the numbers you start with.
This is a bit unsatisfactory because no one cares about the new kind of “mean” involved. And, in fact, it’s a pretty unsatisfactory sort of mean because it’s not an increasing function of its arguments! If we fix a=1 we get b(b+1)/(b^2+1) = 1 + (b-1)/(b^2+1), and for large b this is decreasing, not increasing.
But wait, if that’s true then surely the same must be true for the “contraharmonic mean” which is (so to speak) its mirror image. And so it is. Ch(a,1) = (1+a^2)/(1+a) and when a is very _small_ this is a decreasing, not an increasing, function of a.
These things are all “Lehmer means”. The theorems so far are that an AGM-like iteration with the p,r Lehmer means preserves (and hence converges to) the q’th Lehmer mean, where (p,q,r) is (0,1,2) for HM/ChM->AM, and (-1,0,1) for AM/stupidmean->HM, and (0,1/2,1) for AM/HM->GM. But it _doesn’t_ hold in general for (p,q,r) in arithmetic progression. I don’t know whether it holds for any (p,q,r) other than the three cases above and the trivial ones where p=q=r.