Let P be a parabola. Draw tangents to P at three different points. These three lines intersect to form a triangle.
Theorem: The circumcircle of this triangle passes through the focus of P. [1]
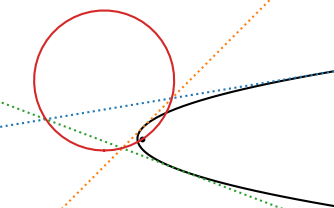
In the image above, the dashed lines are tangents and the black dot is the focus of the parabola.
(See this post for an explanation of what focus and directrix mean.)
By the way, creating the image above required finding the circle through the three intersection points. See the previous post for how to find such a circle.
[1] Ross Honsberger. Episodes in Nineteenth and Twentieth Century Euclidean Geometry. Mathematical Association of America. 1995. Page 47.

Most people probably read this blog for hard math with a strong practical bent. I just read it for the poetry.
And this post, like good poetry, is tightly-crafted and *very* evocative.
Reading this, i instantly thought of the cusp catastrophe (the parabola along the cusp’s edge-on dimension, the rough shape of the triangle as a projection down through the cusp from an orthogonal direction, and the circle, somehow overlaid to illustrate dynamic cusp traversal. I just can’t figure out what meaning the focus (or directrix, for that matter) might have.
Those with a mathematical (instead of poetic) predisposition, may be able to embed these ideas more concretely. Or, more likely, dismiss them quickly as poetry.