Draw three circles of radius r that intersect at a single point. Then draw a triangle connecting the remaining three points of intersection.
(Each pair of circles intersects in two points, one of which is the point where all three circles intersect, so there are three other intersection points.)
Then the circumcircle of the triangle, the circle through the three vertices, also has radius r.
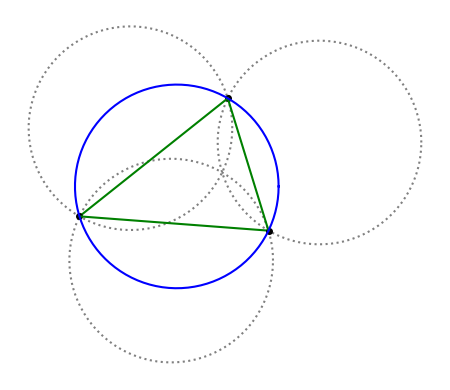
I’ve seen this theorem referred to as Johnson’s theorem, as well as the Johnson–Tzitzeica or Tzitzeica-Johnson theorem. Apparently Roger Johnson and George Tzitzeica (Gheorghe Țițeica) both proved the same theorem around the same time. Johnson’s publication [1] dates to 1916.
It’s remarkable that a theorem in Euclidean geometry this easy to state was discovered 2200 years after Euclid. Johnson says in [1]
Singularly enough, this remarkable theorem appears to be new. A rather cursory search in several of the treatises on modern elementary geometry fails to disclose it, and the author has not yet found any person to whom it was known. On the other hand, the figure is so simple … that it seems almost out of the question that the fact can have escaped detection. Even if geometers have overlooked it, someone must have noticed it in casually drawing circles. But if this were the case, it seems like a theorem of sufficient interest to receive some prominence in the literature, and therefore ought to be well known.
Related posts
[1] Roger Johnson. A circle theorem. The American Mathematical Monthly, May, 1916, Vol. 23, No. 5, pp. 161-162.

Remarkable indeed! Your coloring of the figure makes it easy to see that the sides of the triangle formed by the chords reveal the quasi-symmetry for each of the circles. The dotted arcs on the outside are obviously the same size as their “reflected” arcs of the central blue circle. QED.
Is anything known about the coordinates of the center of this circle? (In relation to those of the 3 circles one started with)