Let Q be a convex quadrilateral with at most two parallel sides. Draw the two diagonals then draw a line through their midpoints. This line is called the Newton line.
(The requirement that at most two sides are parallel insures that the midpoints are distinct and so there is a unique line joining them.)
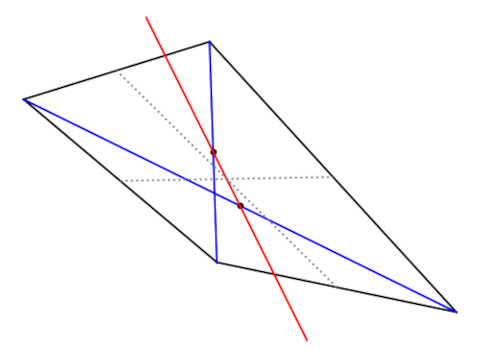
In the figure above, the diagonals are blue, their midpoints are indicated by black dots, and the red line joining them is the Newton line.
Now join the midpoints of the sides. These are draw with dotted gray lines above. Then the intersection of these two lines lies on the Newton line.
Now suppose further that our quadrilateral is a tangential quadrilateral, i.e. that all four sides are tangent to a circle C. Then the center of C also lies on the Newton line.
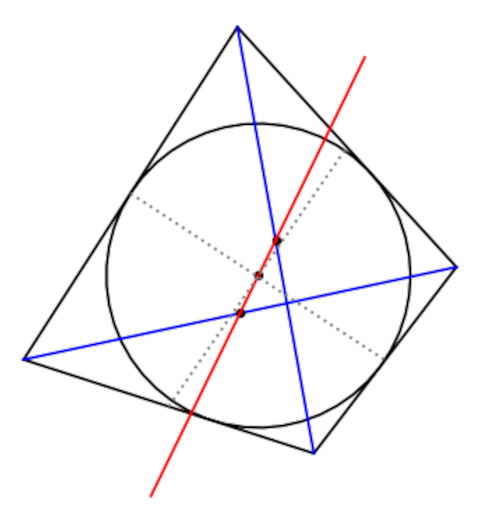
In the image above, it appears that the lines joining the midpoints of the sides also passes intersect at the center of the circle. That’s not true in general, and its not true in the example above but you’d have to zoom in to see it. But it is true that the intersection of these lines and the center of the circle both lie on the Newton line.
