I don’t recall where I read this, but someone recommended that if you need a tool, buy the cheapest one you can find. If it’s inadequate, or breaks, or you use it a lot, then buy the best one you can afford. (Update: Thanks to Jordi for reminding me in the comments that this comes from Kevin Kelly.)
If you follow this strategy, you’ll sometimes waste a little money by buying a cheap tool before buying a good one. But you won’t waste money buying expensive tools that you rarely use. And you won’t waste money by buying a sequence of incrementally better tools until you finally buy a good one.
The advice above was given in the context of tools you’d find in a hardware store, but I’ve been thinking about it in the context of software tools. There’s something to be said for having crude tools that are convenient for small tasks, and sophisticated tools that are appropriate for big tasks, but not investing much in the middle. That’s kind of what I was getting at in my recent post From shell to system.
I’m making a bunch of diagrams for a new project, and the best tool for the job would probably be Adobe Illustrator because professionals routinely use it to make high-quality vector art. But I’m not doing that. I’m drawing ASCII art diagrams, just boxes and arrows drawn in plain text. Something like the drawing below.
+--------------+ compiles to +---+
| Foo language | ----------> | C |
+--------------+ +---+
^
| embeds into
:
+---------+
| Bar DSL |
+---------+
The crude nature of ASCII art is a feature, not a bug. There is no temptation to be precious [*] about the aesthetics since the end product isn’t going to win any design awards in any case. There are compelling incentives to keep the diagrams small and simple. It encourages keeping the focus on content and give up on aesthetics once you hit diminishing return, which occurs fairly quickly.
Drawing ASCII diagrams is clumsy, even with tools that make it easier. Wouldn’t it be faster to use a tool meant for drawing? Well, yes and no. Drawing individual graphic elements would be faster in a drawing tool. But inevitably I’d spend more time on the appearance of the graphs, and so ultimately it would be slower.
The initial motivation for making ASCII diagrams was to keep diagrams and source code in the same file, not to eliminate the temptation to spend too much time tweaking graphics. The latter was a positive unintended consequence.
Related post: Doing good work with bad tools
***
I’m not doing this completely bare-knuckles. Emacs has tools like artist-mode that make it easier than manually positioning every character. And I’m using DITAA sometimes to compile the plain text diagrams into graphics more appropriate for pasting into a report. The example above compiles to the image below.
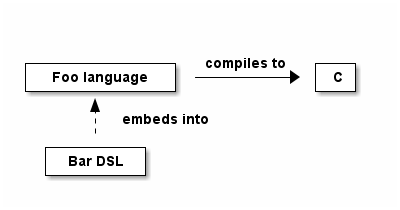
More on how this works here.
***
[*] Not precious as in valuable, but precious as in affectedly or excessively refined. As in filmmaker Darren Doane’s slogan “We are not precious here.”