Machine learning

Why are CUDA kernels hard to optimize?

Posted on by Wayne Joubert

Explosive datacenter demand has caused developers to leave no stone unturned in search of higher efficiencies. The DeepSeek team, not satisfied with Nvidia’s CUDA libraries, used a virtualized form of assembly language (PTX) to write kernel codes to accelerate their AI computations. Others have attempted to generate optimized kernels using AI, though some results have been questioned (for various attempts, see also here, here, here, here and here).

Why is it hard to write peak-speed GPU code? Writing really fast code has always been arduous, but it seems especially so for modern GPUs.

To understand the issues, my colleagues and I performed a detailed study of GPU kernel performance, across eight different GPU models from three GPU vendors [1]. The test case we considered was low precision matrix multiply, a resource-intensive operation for LLM training. We ran many, many experiments to understand what causes performance variability and why kernels sometimes run slower than you’d think they should.

For the cases we studied, we found about half a dozen different factors, but the upshot is this: modern processors like GPUs have become so complex—notably their multi-layered hierarchical memory subsystems—that it is difficult to get consistently high performance across all problem sizes a user might want to run in practice. As a result, the performance for the target problem might be surprisingly and mysteriously less than the advertised peak performance for the operation in question. The reasons might be obvious—like cache line misalignment—or more opaque. For the matrix multiply case, various issues like the need for prefetching, caching, tiling and block size selection, make it difficult for the kernel developer to optimize for every input size a user might specify.

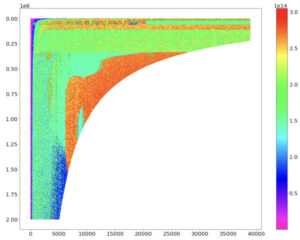
Below is an example graphic from our paper. The color indicates floating point operation rate (FLOPs) for a reduced precision matrix multiply on a representative GPU using a library call. The horizontal and vertical axes refer to the matrix dimensions for the problem (see paper for details). Though some regions show performance near the theoretical peak (red), other immediately adjacent regions show problem sizes that run dramatically less—in fact, only about half of peak performance, or less. Presumably this is because either individual kernel performance or the selection of kernels used by the library is suboptimal. The net outcome is, if your problem lands a “bad” region, you’re in for a big surprise, your performance will be much less than expected, and you may not understand why. All high-performing GPUs we tested showed irregular behaviors such as this [2] [3].

In the past this was not always a problem.  Older architectures like Sun Sparc or Cray vector processor, complex as they were, were simple enough that a reasonably well-tuned computational kernel might run well across most if not all inputs [4]. Today, performance is much harder to predict and can vary substantially based on the requested problem sizes.

This is a tough challenge for library developers. Whenever a new GPU model family comes out, new kernel optimization and tuning are required to give (hopefully) more consistently high performance, and some cases get more developer attention than others due to customer needs and limited developer resources. As a result, infrequently used operations do not get as much attention, but they may be the exact ones you need for your particular case [5].

Tools are available to help optimize for specific cases. The excellent Nvidia CUTLASS library exposes access to many more fine-grained options compared to the standard cuBLAS library. The not faint of heart can try programming Nvidia GPUs at the level of PTX, or (shudder) SASS. Superoptimization might help, but only for very small code fragments and even then there may be too many external factors influencing performance to make it effective.

Autotuning is a promising approach though it doesn’t seem to have reached its full potential in production. AI might really help here [6]; in our own paper we had some success using machine learning methods like decision trees and random forests to model performance as a function of problem size, though our work was exploratory and not production-ready. To make a well-crafted general solution it would seem would require a lot of effort to do right. Code sustainability and maintenance are also critical; a sustainable workflow would be needed to retrain on new GPUs, new CUDA releases and even site-specific and system-specific settings like GPU power and frequency cap policies.

Most recent AI-driven work focuses on optimizing performance for one or a few problem sizes only. A truly production-quality general purpose tool would give both 100% accurate results and also top achievable performance for any input problem size (even for corner cases) or data type. This would require both optimized GPU kernels and optimal kernel dispatcher for kernel selection. And the method would need to be robust to issues like power and frequency variabilities in production runs. This would seem to currently be an unsolved problem. Solving it would be of huge benefit to the hyperscaler community.

Notes

[1] For related work from a slightly different angle, see this excellent work from Matt Sinclair’s lab.

[2] It turned out this study was helpful to us for production runs, to help us to triage an odd performance conundrum we encountered when attempting an exascale run (see here, here).

[3] Incidentally this example shows the hazards of simplistic benchmark suites to measure GPU code performance. Unless the benchmark captures a truly large and varied set of input cases, any new optimization method proposed can artificially “overfit” performance on the tests and still underperform miserably on many user cases of interest.

[4] I once wrote a 1-D wavelet convolution kernel for a Sparc processor, using a circular register buffer and loop unrolling to minimize loads and stores, this achieving near-peak performance. The code was correctly compiled from C to assembly, and performance for a given problem was almost precisely predictable. That was before the days of complex memory hierarchies.

[5] One vendor I know of used to take customer requests for hand tuning expensive library calls and made them run fast at the specific customer problem sizes.

[6] LLM kernel generation seems like a natural fit, particularly since LLM-generated code quality has much improved in recent months. Kernel selection and parameter selection for block size, tiling etc. might be better solved by direct training of machine learning models, or methods like this. Comparative studies on this would be informative.

 

Using TF-IDF to pick out important words

Posted on by John

TF-IDF (Term Frequency-Inverse Document Frequency) is commonly used in natural language processing to extract important words. The idea behind the statistic is that a word is important if it occurs frequently in a particular document but not frequently in the corpus of documents the document came from.

The term-frequency (TF) of a word in a document is the probability of selecting that word at random from the document, i.e. the number of times the word appears in the document divided by the total number of words in the document.

Inverse document frequency (IDF) is not quite what the name implies. You might reasonably assume that inverse document frequency is the inverse (i.e. reciprocal) of document frequency, where document frequency is the proportion of documents containing the word. Or in other words, the reciprocal of the probability of selecting a document at random containing the word. That’s almost right, except you take the logarithm.

TF-IDF for a word and a document is the product of TF and IDF for that word and document. You could say

TF-IDF = TF * IDF

where the “-” on the left side is a hyphen, not a minus sign.

To try this out, let’s look at the King James Bible. The text is readily available, for example from Project Gutenberg, and it divides into 66 documents (books).

Note that if a word appears in every document, in our case every book of the Bible, then IDF = log(1) = 0. This means that common words like “the” and “and” that appear in every book get a zero score.

Here are the most important words in Genesis, as measured by TF-IDF.

laban: 0.0044
abram: 0.0040
joseph: 0.0037
jacob: 0.0034
esau: 0.0032
rachel: 0.0031
said: 0.0031
pharaoh: 0.0030
rebekah: 0.0029
duke: 0.0028

It’s surprising that Laban comes out on top. Surely Joseph is more important than Laban, for example. Joseph appears more often in Genesis than does Laban, and so has a higher TF score. But Laban only appears in two books, whereas Joseph appears in 23 books, and so Laban has a higher IDF score.

Note that TF-IDF only looks at sequences of letters. It cannot distinguish, for example, the person named Laban in Genesis from the location named Laban in Deuteronomy.

Another oddity above is the frequency of “duke.” In the language of the KJV, a duke was the head of a clan. It wasn’t a title of nobility as it is in contemporary English.

The most important words in Revelation are what you might expect.

angel: 0.0043
lamb: 0.0034
beast: 0.0033
throne: 0.0028
seven: 0.0028
dragon: 0.0025
angels: 0.0025
bottomless: 0.0024
overcometh: 0.0023
churches: 0.0022

You can find the top 10 words in each book here.

Related posts

Machine learning by satisfiability solving

Posted on by Wayne Joubert

Define B = {0, 1} and a Boolean function fp: BN → B where p is a Boolean parameter vector in Bn. Consider that fp(x) can be represented as a Boolean expression whose variables are the entries of vectors p and x. Assume that c is the cost of computing fp(x) measured in some way, for example, the number of operator evaluations based on some complete set of Boolean operators. Then, given y in B and x in BN, the cost to solve the equation fp(x) = y for satisfying y has cost c2n, using the most naïve brute force search.

For 3SAT solving, a much better worst case bound is known, namely O(1.307n), see here, for a related discussion see here. For the inexactly-defined class of “industrial problems,” performance in practice is often much better; for a discussion see here.

Now consider a set of Boolean feature vectors xi and labels yi. for i in {1, …, d}. One can now solve fp(xi) = yi for all i. Since the number of unknown variables to be solved for is unchanged, the naïve bound on computational cost is cd2n, scaling linearly in the number of data values d. Note this is tractable if the phenomenon in question can be modeled by a small number of logical parameters n.

In practice, one generally does not solve a machine learning problem exactly but approximately, minimizing a loss function. One can use the AtLeast operator in a SAT solver like Z3 to require that fp(xi) = yi be satisfied for at least K values of i, for some K. One can then find the maximal such K by performing bisection on K, requiring log2(d) such SAT solves. On exact solvers for this problem see also here.

The AtLeast operator can be implemented by either binary adder / totalizer encoding (Bailleux and Boufkhad 2003), sequential counter encoding (Sinz 2005), or Batcher sorting network approach (Abío et al. 2013). Unfortunately, all these methods require adding significant numbers of auxiliary variables, adversely affecting the naïve complexity bound. However, one can hope that performance is much better than this bound for industrial problems, as is often the case in practice. Furthermore, randomized approximation algorithms known to run in polynomial time can provably find assignments that satisfy a guaranteed fraction (e.g., 3/4 or more) of the maximum number of satisfiable Boolean constraints (see for example here, here, here and here). This might serve as a proxy for exactly solving for the optimizer.

If the problem instead has Boolean expressions with embedded linear inequality predicates on integer variables of bounded range, one could apply SMT solver methods directly using the ideas described above, or convert the problem to a SAT problem and apply the above methods directly.

The idea of using SAT solvers for machine learning in the way described here goes back to (Kamath et al. 1992). The method is described with an example in Donald Knuth’s TAOCP fascicle on Satisfiability, section on Learning a Boolean function.

Why do LLMs have emergent properties?

Posted on by Wayne Joubert

Large language models display emergence behaviors: when the parameter count is scaled to a certain value, suddenly the LLM is capable of performing a new task not possible at a smaller size. Some say the abruptness of this change is merely a spurious artifact of how it is measured. Even so, many would like to understand, predict, and even facilitate the emergence of these capabilities.

The following is not a mathematical proof , but a plausibility argument as to why such behavior should not be surprising, and a possible mechanism. I’ll start with simple cases and work up to more complex ones.

In nature

An obvious point. Emergence is ubiquitous in nature. Ice near the freezing point that is slightly heated suddenly becomes drinkable (phase change). An undrivable car with three wheels gets a fourth wheel and is suddenly drivable. Nonlinearity exists in nature.

In machine learning

A simple example: consider fitting N arbitrary points in one dimension with linear regression using monomials. For a basis up to degree less than N-1, for most possible sets of data points (excluding “special” cases like collinear), the regression error will be non-zero, and reciprocally, the accuracy will be some finite value. Increase the number of monomials (parameter count) to N-1, and suddenly the error drops to zero, and accuracy jumps to infinity.

When using k-means clustering, if one has n clusters and runs k-means clustering with K<N cluster centers, the error will be significant, but when K=N, suddenly the cluster centers can model all clusters well, and the error drops dramatically.

In algorithms

Consider all Boolean circuits composed from some fixed logically complete set of gate types. Now consider the goal of constructing a Boolean circuit that takes a single byte representing the integer N and increments it to N+1, modulo 256 (8 bits input, 8 bits output). Clearly, such a circuit exists, for example, the standard chain of 1-bit add-and-carry circuits. Note one can in principle enumerate all possible circuits of finite gate count. It is manifest that an integer K>0 exists for which no circuit with less than K gates solves the problem but there exists a circuit with K gates that does. The standard chain of 8 1-bit adders might be such a minimizer, or maybe the optimal circuit is more exotic (for example see here, though this method is not guaranteed to compute a minimizer).

One would thus see this capability potentially emerge as soon as one reaches a gate budget of K gates. Now, one could argue that for a smaller gate budget, a partial result might be possible, for example, incrementing any 7-bit number—so the increase in capability is continuous, not emergent or wholly new. However, if all you care about is correctly incrementing any byte (for example, for manipulating ASCII text), then it’s all or nothing; there’s no partial credit. Even so, the gate budget required for incrementing 8 bits compared to only 7-bit integers is only slightly higher, but this minor increase in gate count actually doubles the quantity of integers that can be incremented, which might be perceived as a surprising, unexpected (emergent) jump.

In LLMs

The parameter count of an LLM defines a certain bit budget. This bit budget must be spread across many, many tasks the final LLM will be capable of, as defined by the architecture and the training process (in particular, the specific mix of training data). These tasks are implemented as “algorithms” (circuits) within the LLM. The algorithms are mixed together and (to some extent) overlap in a complex way that is difficult to analyze.

Suppose one of these desired capabilities is some task X. Suppose all possible input/output pairs for this operation are represented in the training data (or, maybe not—maybe some parts of the algorithm can be interpolated from the training data). The LLM is trained with SGD, typically with 2-norm minimization. The unit ball in the 2-norm is a sphere in high dimensional space. Thus “all directions” of the loss are pressed down equally by the minimization process—which is to say, the LLM is optimized on all the inputs for many, many tasks, not just task X. The limited parameter bit budget must be spread across many, many other tasks the LLM must be trained to do. As LLMs of increasing size are trained, at some point enough parameter bits in the budget will be allocatable to represent a fully accurate algorithm for task X, and at this point the substantially accurate capability to do “task X” will be perceivable—“suddenly.”

Task X could be the 8-bit incrementer, which from an optimal circuit standpoint would manifest emergence, as described above. However, due to the weakness of the SGD training methodology and possibly the architecture, there is evidence that LLM training does not learn optimal arithmetic circuits at all but instead does arithmetic by a “bag of heuristics” (which incidentally really is, itself, an algorithm, albeit a piecemeal one). In this case, gradually adding more and more heuristics might be perceived to increase the number of correct answers in a somewhat more incremental way, to be sure. However, this approach is not scalable—to perform accurate arithmetic for any number of digits, if one does not use an exact arithmetic algorithm or circuit, one must use increasingly more heuristics to increase coverage to try to capture all possible inputs accurately. And still, transitioning from an approximate to an exact 8-bit incrementer might in practice be perceived as an abrupt new capability, albeit a small one for this example.

One could alternatively consider tool use (for example, a calculator function that is external to the LLM proper), but then a new tool must be written for every new task, and the LLM needs to understand how to use the tool. (Maybe at some point LLMs will know how to write and use their own algorithmic tools?)

Predicting emergence

The real question is how can we predict when a new LLM will achieve some new capability X. For example, X = “Write a short story that resonates with the social mood of the present time and is a runaway hit” (and do the same thing again once a year based on new data, indefinitely into the future without failure). We don’t know an “algorithm” for this, and we can’t even begin to guess the required parameter budget or the training data needed. That’s the point of using an LLM—its training internally “discovers” new, never seen before algorithms from data that would be difficult for humans to formulate or express from first principles. Perhaps there is some indirect way of predicting the emergence of such X, but it doesn’t seem obvious on the face of it how to predict this directly.

Conclusion

Based on these examples, it would seem not at all surprising for LLMs to exhibit emergent behaviors, though in our experience our encounter with them may be startling. Predicting them may be possible to a limited extent but for the general case seems really hard.

Do you have any thoughts? If so, please leave them in the comments.

Looking at Your Data

Posted on by Wayne Joubert

What to do first after scoping out and starting a data science project?

I’ve started an unsupervised learning project based on textual data. The first thing I like to do is actually look at the data. Is it noisy? What are the features—complex feature engineering needed? How heterogeneous? What generalization and overfitting challenges?

Analysis can take many forms: actually looking at the numbers, using visualization tools, Excel spreadsheet, Jupyter notebooks with Matplotlib, computing various statistics on the whole dataset or portions of it.

Some may believe this is not important. Just throw a barrage of classification or regression methods at the data, treat the data as a black box. Of course testing on a suite of ML methods is not a bad thing. But I can’t imagine not using every avenue available, including looking at the data. I’m certainly not alone in this view (see for example here, here and here).

I spent a few hours developing a simple custom data viewer for my problem that colored different parts of the textual data to give insight as to what was going on. I used ChatGPT to develop parts of this tool; some of it was incorrect and needed fixing, but having at least a draft of the code definitely saved time. Seeing the actual data in person was insightful and generated ideas for solving the problem.

While inspecting the data can help identify issues, it also risks biasing the modeling process by imposing assumptions that a flexible model might otherwise uncover on its own. One must also beware of data leakage. That being said—in general I think understanding as much as you can about the data is not a bad thing.

Can AI Models Reason: Is Data All You Need?

Posted on by Wayne Joubert

Many are voicing concern that the world is running out of data and that this will be a blocker to progress toward smarter AI models. One paper in fact projects timelines for when we will run out.

AI researchers are looking for ways to adapt.  Nvidia has trained a specific model to generate synthetic data for training other models. Some use this approach, though using AI-generated data to train AI is not without risk.

Others have asked a bigger question, namely, is something fundamentally missing in our approach that relies so heavily on data. Certainly the bitter lesson thesis and the position long advocated by Geoffrey Hinton argue for a data-first approach with “as few” prior assumptions as possible (though every model has a bias).

But it’s currently simply unknown whether just adding more data and compute will do the trick for achieving general intelligence or whether something else is needed. Neurosymbolic approaches are being experimented with, in various forms. But it’s unclear whether these can scale up to the level needed. And the frontier labs, laser-focused on the current paradigm, may not have adequate time or resources to investigate high-risk/high-reward alternatives.

From a theoretical standpoint, sometimes more data is simply not enough. As discussed in a previous post, some problems in mathematics and engineering require exponentially large amount of data to train neural network models. Exponentials can work in your favor, but also can work against you (think of the Tower of Hanoi problem or the Wheat and Chessboard problem). Some problems on certain models cannot be solved by any amount of data available in the entire universe.

The requirements for solving these problems can grow much more quickly than expected. The strength of neural networks, their flexibility, their universal approximation property, can also be a weakness. It can take so much data to nail down all the parameters so that the model is completely error free. Thankfully, many other problems that people want to solve (such as human language modeling) are fundamentally lower dimensional and thus less vulnerable to this problem.

We just don’t know whether the current data-hungry approach will be enough—or whether we’ll need to learn another bitter lesson.

How hard is constraint programming?

Posted on by Wayne Joubert

I’ve been writing code for the Z3 SMT solver for several months now. Here are my findings.

Python is used here as the base language. Python/Z3 feels like a two-layer programming model—declarative code for Z3, imperative code for Python. In this it seems reminiscent of C++/CUDA programming for NVIDIA GPUs—in that case, mixed CPU and GPU imperative code. Either case is a clever combination of methodologies that is surprisingly fluent and versatile, albeit not a perfect blend of seamless conceptual cohesion.

Other comparisons:

  • Both have two separate memory spaces (CUDA CPU/GPU memories for one; pure Python variables and Z3 variables for the other).
  • Both can be tricky to debug. In earlier days, CUDA had no debugger, so one had to fall back to the trusty “printf” statement (for a while it didn’t even have that!). If the code crashed, you might get no output at all. To my knowledge, Z3 has no dedicated debugger. If the problem being solved comes back as satisfiable, you can print out the discovered model variables, but if satisfiability fails, you get very little information. Like some other novel platforms, something of a “black box.”
  • In both cases, programmer productivity can be well-served by developing custom abstractions. I developed a Python class to manage multidimensional arrays of Z3 variables, this was a huge time saver.

There are differences too, of course.

  • In Python, “=” is assignment, but in Z3, one only has “==”, logical or numeric equality, not assignment per se. Variables are set once and can’t be changed—sort of a “write-once variables” programming model—as is natural to logic programming.
  • Code speed optimization is challenging. Code modifications for Z3 constraints/variables can have extreme and unpredictable runtime effects, so it’s hard to optimize. Z3 is solving an NP-complete problem after all, so runtimes can theoretically increase massively. Speedups can be massive also; one round of changes I made gave 2000X speedup on a test problem. Runtime of CUDA code can be unpredictable to a lesser degree, depending on the PTX and SASS code generation phases and the aggressive code optimizations of the CUDA compiler. However, it seems easier to “see through” CUDA code, down to the metal, to understand expected performance, at least for smaller code fragments. The Z3 solver can output statistics of the solve, but these are hard to actionably interpret for a non-expert.
  • Z3 provides many, many algorithmic tuning parameters (“tactics”), though it’s hard to reason about which ones to pick. Autotuners like FastSMT might help. Also there have been some efforts to develop tools to visualize the solve process, this might be of help.

It would be great to see more modern tooling support and development of community best practices to help support Z3 code developers.

Getting some (algorithmic) SAT-isfaction

Posted on by Wayne Joubert

How can you possibly solve a mission-critical problem with millions of variables—when the worst-case computational complexity of every known algorithm for that problem is exponential in the number of variables?

SAT (Satisfiability) solvers have seen dramatic orders-of-magnitude performance gains for many problems through algorithmic improvements over the last couple of decades or so. The SAT problem—finding an assignment of Boolean variables that makes a given Boolean expression true—represents the archetypal NP-complete problem and in the general case is intractable.

However, for many practical problems, solutions can be found very efficiently by use of modern methods. This “killer app” of computer science, as described by Donald Knuth, has applications to many areas, including software verification, electronic design automation, artificial intelligence, bioinformatics, and planning and scheduling.

Its uses are surprising and diverse, from running billion dollar auctions to solving graph coloring problems to computing solutions to Sudoku puzzles. As an example, I’ve included a toy code below that uses SMT, a relative of SAT, to find the English language suffix rule for regular past tense verbs (“-ed”) from data.

When used as a machine learning method, SAT solvers are quite different from other methods such as neural networks. SAT solvers can for some problems have long or unpredictable runtimes (though MAXSAT can sometimes relax this restriction), whereas neural networks have essentially fixed inference cost (though looping agent-based models do not).

On the other hand, answers from SAT solvers are always guaranteed correct, and the process is interpretable; this is currently not so for neural network-based large language models.

To understand better how to think about this difference in method capabilities, we can take a lesson from the computational science community. There, it is common to have a well-stocked computational toolbox of both slow, accurate methods and fast, approximate methods.

In computational chemistry, ab initio methods can give highly accurate results by solving Schrödinger’s equation directly, but only scale to limited numbers of atoms. Molecular dynamics (MD), however, relies more on approximations, but scales efficiently to many more atoms. Both are useful in different contexts. In fact, the two methodologies can cross-pollenate, for example when ab initio calculations are used to devise force fields for MD simulations.

A lesson to take from this is, it is paramount to find the best tool for the given problem, using any and all means at one’s disposal.

The following are some of my favorite general references on SAT solvers:

It would seem that unless P = NP, commonly suspected to be false, the solution of these kinds of problems for any possible input is hopelessly beyond reach of even the world’s fastest computers. Thankfully, many of the problems we care about have an internal structure that makes them much more solvable (and likewise for neural networks). Continued improvement of SAT/SMT methods, in theory and implementation, will greatly benefit the effective solution of these problems.

A toy example: find the English past tense suffix rule using Z3

import csv
import z3

def char2int(c): return ord(c) - ord('a')

def int2char(i): return chr(i + ord('a'))

# Access the language data from the file.
with open('eng_cols.txt', newline='') as csvfile:
    reader = csv.reader(csvfile, delimiter='\t')
    table = [row for row in reader]

nrow, ncol = len(table), len(table[0])

# Identify which columns of input table have stem and targeted word form.
stem_col, form_col = 0, 1

# Calculate word lengths.
nstem = [len(table[i][stem_col]) for i in range(nrow)]
nform = [len(table[i][form_col]) for i in range(nrow)]

# Length of suffix being sought.
ns = 2

# Initialize optimizer.
solver = z3.Optimize()

# Define variables to identify the characters of suffix; add constraints.
var_suf = [z3.Int(f'var_suf_{i}') for i in range(ns)]

for i in range(ns):
    solver.add(z3.And(var_suf[i] >= 0, var_suf[i] < 26))

# Define variables to indicate whether the given word matches the rule.
var_m = [z3.Bool(f'var_m_{i}') for i in range(nrow)]

# Loop over words.
for i in range(nrow):

    # Constraint on number of characters.
    constraints = [nform[i] == nstem[i] + ns]

    # Constraint that the form contains the stem.
    for j in range(nstem[i]):
        constraints.append(
            table[i][stem_col][j] == table[i][form_col][j]
                if j < nform[i] else False)

    # Constraint that the end of the word form matches the suffix. 
    for j in range(ns):
        constraints.append(
            char2int(table[i][form_col][nform[i]-1-j]) == var_suf[j]
                if j < nform[i] else False)

    # var_m[i] is the "and" of all these constraints.
    solver.add(var_m[i] == z3.And(constraints))

# Seek suffix that maximizes number of matches.
count = z3.Sum([z3.If(var_m[i], 1, 0) for i in range(nrow)])
solver.maximize(count)

# Run solver, output results.
if solver.check() == z3.sat:
    model = solver.model()
    suf = [model[var_suf[i]] for i in range(ns)]
    print('Suffix identified: ' +
          ''.join(list([int2char(suf[i].as_long())
                        for i in range(ns)]))[::-1])
    print('Number of matches: ' + str(model.evaluate(count)) +
          ' out of ' + str(nrow) + '.')

    var_m_values = [model[var_m[i]] for i in range(nrow)]

    print('Matches:')
    for i in range(nrow):
        if var_m_values[i]:
            print(table[i][stem_col], table[i][form_col])

The search for the perfect prompt

Posted on by Wayne Joubert

Anyone with more than casual experience with ChatGPT knows that prompt engineering is a thing. Minor or even trivial changes in a chatbot prompt can have significant effects, sometimes even dramatic ones, on the output [1]. For simple requests it may not make much difference, but for detailed requests it could matter a lot.

Industry leaders said they thought this would be a temporary limitation. But we are now a year and a half into the GPT-4 era, and it’s still a problem. And since the number of possible prompts has scaling that is exponential in the prompt length, it can sometimes be hard to find a good prompt given the task.

One proposed solution is to use search procedures to automate the prompt optimization / prompt refinement process. Given a base large language model (LLM) and an input (a prompt specification, commonly with a set of prompt/answer pair samples for training), a search algorithm seeks the best form of a prompt to use to elicit the desired answer from the LLM.

This approach is sometimes touted [2] as a possible solution to the problem. However, it is not without  limitations.

A main one is cost. With this approach, one search for a good prompt can take many, many trial-and-error invocations of the LLM, with cost measured in dollars compared to the fraction of a cent cost of a single token of a single prompt. I know of one report of someone who does LLM prompting with such a tool full time for his job, at cost of about $1,000/month (though, for certain kinds of task, one might alternatively seek a good prompt “template” and reuse that across many near-identical queries, to save costs).

This being said, it would seem that for now (depending on budget) our best option for difficult prompting problems is to use search-based prompt refinement methods. Various new tools have come out recently (for example, [3-6]). The following is a report on some of my (very preliminary) experiences with a couple of these tools.

PromptAgent

The first is PromptAgent [5]. It’s a research code available on GitHub. The method is based on Monte Carlo tree search (MCTS), which tries out multiple chains of modification of a seed prompt and pursues the most promising. MCTS can be a powerful method, being part of the AlphaGo breakthrough result in 2016.

I ran one of the PromptAgent test problems using GPT-4/GPT-3.5 and interrupted it after it rang up a couple of dollars in charges. Looking at the logs, I was somewhat amazed that it generated long detailed prompts that included instructions to the model for what to pay close attention to, what to look out for, and what mistakes to avoid—presumably based on inspecting previous trial prompts generated by the code.

Unfortunately, PromptAgent is a research code and not fully productized, so it would take some work to adapt to a specific user problem.

DSPy

DSPy [6] on the other hand is a finished product available for general users. DSPy is getting some attention lately not only as a prompt optimizer but also more generally as a tool for orchestrating multiple LLMs as agents. There is not much by way of simple examples for how to use the code. The website does have an AI chatbot that can generate sample code, but the code it generated for me required significant work to get it to behave properly.

I ran with the MIPRO optimizer which is most well-suited to prompt optimization. My experience with running the code was that it generated many random prompt variations but did not do in-depth prompt modifications like PromptAgent. PromptAgent does one thing, prompt refinement, and must do it well, unlike DSPy which has multiple uses. DSPy would be well-served to have implemented more powerful prompt refinement algorithms.

Conclusion

I would wholeheartedly agree that it doesn’t seem right for an LLM would be so dependent on the wording of a prompt. Hopefully, future LLMs, with training on more data and other improvements, will do a better job without need for such lengthy trial-and-error processes.

References

[1]  “Quantifying Language Models’ Sensitivity to Spurious Features in Prompt Design or: How I learned to start worrying about prompt formatting,” https://openreview.net/forum?id=RIu5lyNXjT

[2] “AI Prompt Engineering Is Dead” (https://spectrum.ieee.org/prompt-engineering-is-dead, March 6, 2024

[3]  “Evoke: Evoking Critical Thinking Abilities in LLMs via Reviewer-Author Prompt Editing,” https://openreview.net/forum?id=OXv0zQ1umU

[4] “Large Language Models as Optimizers,” https://openreview.net/forum?id=Bb4VGOWELI

[5] “PromptAgent: Strategic Planning with Language Models Enables Expert-level Prompt Optimization,” https://openreview.net/forum?id=22pyNMuIoa

[6] “DSPy: Compiling Declarative Language Model Calls into State-of-the-Art Pipelines,” https://openreview.net/forum?id=sY5N0zY5Od

 

Hallucinations of AI Science Models

Posted on by Wayne Joubert

AlphaFold 2, FourCastNet and CorrDiff are exciting. AI-driven autonomous labs are going to be a big deal [1]. Science codes now use AI and machine learning to make scientific discoveries on the world’s most powerful computers [2].

It’s common practice for scientists to ask questions about the validity, reliability and accuracy of the mathematical and computational methods they use. And many have voiced concerns about the lack of explainability and potential pitfalls of AI models, in particular deep neural networks (DNNs) [3].

The impact of this uncertainty varies highly according to project. Science projects that are able to easily check AI-generated results against ground truth may not be that concerned. High-stakes projects like design of a multimillion dollar spacecraft with high project risks may ask about AI model accuracy with more urgency.

Neural network accuracy

Understanding of the properties of DNNs is still in its infancy, with many as-yet unanswered questions. However, in the last few years some significant results have started to come forth.

A fruitful approach to analyzing DNNs is to see them as function approximators (which, of course, they are). One can study how accurately DNNs approximate a function representing some physical phenomenon in a domain (for example, fluid density or temperature).

The approximation error can be measured in various ways. A particularly strong measure is “sup-norm” or “max-norm” error, which requires that the DNN approximation be accurate at every point of the target function’s domain (“uniform approximation”). Some science problems may have a weaker requirement than this, such as low RMS or 2-norm error. However, it’s not unreasonable to ask about max-norm approximation behaviors of numerical methods [4,5].

An illuminating paper by Ben Adcock and Nick Dexter looks at this problem [6]. They show that standard DNN methods applied even to a simple 1-dimensional problem can result in “glitches”: the DNN as a whole matches the function well but at some points totally misapproximates the target function. For a picture that shows this, see [7].

Other mathematical papers have subsequently shed light on these behaviors. I’ll try to summarize the findings below, though the actual findings are very nuanced, and many details are left out here. The reader is advised to refer to the respective papers for exact details.

The findings address three questions: 1) how many DNN parameters are required to approximate a function well? 2) how much data is required to train to a desired accuracy? and 3) what algorithms are capable of training to the desired accuracy?

How many neural network weights are needed?

How large does the neural network need to be for accurate uniform approximation of functions? If tight max-norm approximation requires an excessively large number of weights, then use of DNNs is not computationally practical.

Some answers to this question have been found—in particular, a result 1 is given in [8, Theorem 4.3; cf. 9, 10]. This result shows that the number of neural network weights required to approximate an arbitrary function to high max-norm accuracy grows exponentially in the dimension of the input to the function.

This dependency on dimension is no small limitation, insofar as this is not the dimension of physical space (e.g., 3-D) but the dimension of the input vector (such as the number of grid cells), which for practical problems can be in the tens [11] or even millions or more.

Sadly, this rules out the practical use of DNN for some purposes. Nonetheless, for many practical applications of deep learning, the approximation behaviors are not nearly so pessimistic as this would indicate (cp. [12]). For example, results are more optimistic:

  • if the target function has a strong smoothness property;
  • if the function is not arbitrary but is a composition of simpler functions;
  • if the training and test data are restricted to a (possibly unknown) lower dimensional manifold in the high dimensional space (this is certainly the case for common image and language modeling tasks);
  • if the average case behavior for the desired problem domain is much better than the worst case behavior addressed in the theorem;
  • The theorem assumes multilayer perceptron and ReLU activation; other DNN architectures may perform better (though the analysis is based on multidimensional Taylor’s theorem, which one might conjecture applies also to other architectures).
  • For many practical applications, very high accuracy is not a requirement.
  • For some applications, only low 2-norm error is sufficient, (not low max-norm).
  • For the special case of physics informed neural networks (PINNs), stronger results hold.

Thus, not all hope is lost from the standpoint of theory. However, certain problems for which high accuracy is required may not be suitable for DNN approximation.

How much training data is needed?

Assuming your space of neural network candidates is expressive enough to closely represent the target function—how much training data is required to actually find a good approximation?

A result 2 is given in [13, Theorem 2.2] showing that the number of training samples required to train to high max-norm accuracy grows, again, exponentially in the dimension of the input to the function.

The authors concede however that “if additional problem information about [the target functions] can be incorporated into the learning problem it may be possible to overcome the barriers shown in this work.” One suspects that some of the caveats given above might also be relevant here. Additionally, if one considers 2-norm error instead of max-norm error, the data requirement grows polynomially rather than exponentially, making the training data requirement much more tractable. Nonetheless, for some problems the amount of data required is so large that attempts to “pin down” the DNN to sufficient accuracy become intractable.

What methods can train to high accuracy?

The amount of training data may be sufficient to specify a suitable neural network. But, will standard methods for finding the weights of such a DNN be effective for solving this difficult nonconvex optimization problem?

A recent paper [14] from Max Tegmark’s group empirically studies DNN training to high accuracy. They find that as the input dimension grows, training to very high accuracy with standard stochastic gradient descent methods becomes difficult or impossible.

They also find second order methods perform much better, though these are more computationally expensive and have some difficulty also when the dimension is higher. Notably, second order methods have been used effectively for DNN training for some science applications [15]. Also, various alternative training approaches have been tried to attempt to stabilize training; see, e.g., [16].

Prospects and conclusions

Application of AI methods to scientific discovery continues to deliver amazing results, in spite of lagging theory. Ilya Sutskever has commented, “Progress in AI is a game of faith. The more faith you have, the more progress you can make” [17].

Theory of deep learning methods is in its infancy. The current findings show some cases for which use of DNN methods may not be fruitful, Continued discoveries in deep learning theory can help better guide how to use the methods effectively and inform where new algorithmic advances are needed.

Footnotes

1 Suppose the function to be approximated takes d inputs and has the smoothness property that all nth partial derivatives are continuous (i.e., is in Cn(Ω) for compact Ω). Also suppose a multilayer perceptron with ReLU activation functions must be able to approximate any such function to max-norm no worse than ε. Then the number of weights required is at least a fixed constant times (1/ε)d/(2n).

2 Let F be the space of all functions that can be approximated exactly by a broad class of ReLU neural networks. Suppose there is a training method that can recover all these functions up to max-norm accuracy bounded by ε. Then the number of training samples required is at least a fixed constant times (1/ε)d.

References

[1] “Integrated Research Infrastructure Architecture Blueprint Activity (Final Report 2023),” https://www.osti.gov/biblio/1984466.

[2] Joubert, Wayne, Bronson Messer, Philip C. Roth, Antigoni Georgiadou, Justin Lietz, Markus Eisenbach, and Junqi Yin. “Learning to Scale the Summit: AI for Science on a Leadership Supercomputer.” In 2022 IEEE International Parallel and Distributed Processing Symposium Workshops (IPDPSW), pp. 1246-1255. IEEE, 2022, https://www.osti.gov/biblio/2076211.

[3] “Reproducibility Workshop: The Reproducibility Crisis in ML‑based Science,” Princeton University, July 28, 2022, https://sites.google.com/princeton.edu/rep-workshop.

[4] Wahlbin, L. B. (1978). Maximum norm error estimates in the finite element method with isoparametric quadratic elements and numerical integration. RAIRO. Analyse numérique, 12(2), 173-202, https://www.esaim-m2an.org/articles/m2an/pdf/1978/02/m2an1978120201731.pdf

[5] Kashiwabara, T., & Kemmochi, T. (2018). Maximum norm error estimates for the finite element approximation of parabolic problems on smooth domains. https://arxiv.org/abs/1805.01336.

[6] Adcock, Ben, and Nick Dexter. “The gap between theory and practice in function approximation with deep neural networks.” SIAM Journal on Mathematics of Data Science 3, no. 2 (2021): 624-655, https://epubs.siam.org/doi/10.1137/20M131309X.

[7] “Figure 5 from The gap between theory and practice in function approximation with deep neural networks | Semantic Scholar,” https://www.semanticscholar.org/paper/The-gap-between-theory-and-practice-in-function-Adcock-Dexter/156bbfc996985f6c65a51bc2f9522da2a1de1f5f/figure/4

[8] Gühring, I., Raslan, M., & Kutyniok, G. (2022). Expressivity of Deep Neural Networks. In P. Grohs & G. Kutyniok (Eds.), Mathematical Aspects of Deep Learning (pp. 149-199). Cambridge: Cambridge University Press. doi:10.1017/9781009025096.004, https://arxiv.org/abs/2007.04759.

[9] D. Yarotsky. Error bounds for approximations with deep ReLU networks. Neural Netw., 94:103–114, 2017, https://arxiv.org/abs/1610.01145

[10] I. Gühring, G. Kutyniok, and P. Petersen. Error bounds for approximations with deep relu neural networks in Ws,p norms. Anal. Appl. (Singap.), pages 1–57, 2019, https://arxiv.org/abs/1902.07896

[11] Matt R. Norman, “The MiniWeather Mini App,” https://github.com/mrnorman/miniWeather

[12] Lin, H.W., Tegmark, M. & Rolnick, D. Why Does Deep and Cheap Learning Work So Well?. J Stat Phys 168, 1223–1247 (2017). https://doi.org/10.1007/s10955-017-1836-5

[13] Berner, J., Grohs, P., & Voigtlaender, F. (2022). Training ReLU networks to high uniform accuracy is intractable. ICLR 2023, https://openreview.net/forum?id=nchvKfvNeX0.

[14] Michaud, E. J., Liu, Z., & Tegmark, M. (2023). Precision machine learning. Entropy, 25(1), 175, https://www.mdpi.com/1099-4300/25/1/175.

[15] Markidis, S. (2021). The old and the new: Can physics-informed deep-learning replace traditional linear solvers?. Frontiers in big Data, 4, 669097, https://www.frontiersin.org/articles/10.3389/fdata.2021.669097/full

[16] Bengio, Y., Lamblin, P., Popovici, D., & Larochelle, H. (2006). Greedy layer-wise training of deep networks. Advances in neural information processing systems, 19,  https://papers.nips.cc/paper_files/paper/2006/hash/5da713a690c067105aeb2fae32403405-Abstract.html

[17] “Chat with OpenAI CEO and Co-founder Sam Altman, and Chief Scientist Ilya Sutskever,” https://www.youtube.com/watch?v=mC-0XqTAeMQ&t=250s