Artificial intelligence

Grokking the James Bond chord

Posted on by John

The last chord of the James Bond theme is known as the James Bond chord. If you’ve ever seen a Bond movie, you’ll recognize it. Here’s a quick video showing how to play it on guitar.

I tried asking Grok 3 to generate some LilyPond code for sheet music a few days ago. LilyPond is pretty obscure as programming languages go—it’s not like asking for Python code—so I was skeptical, but Grok did well.

This afternoon I asked Grok to create sheet music for the James Bond chord. Specifically, I asked

  1. What is the “James Bond chord”?
  2. Create sheet music for the James Bond chord using Lilypond.
  3. Move the chord up an octave.

Here’s the output of each step.

What is the chord?

According to Grok,

The “James Bond chord” is a distinctive musical chord famously associated with the James Bond film franchise. It’s not just a single chord but rather a specific voicing and progression that evokes a sense of mystery, danger, and sophistication—perfectly matching the suave spy’s persona. Officially, it’s often identified as an E minor major 9 chord (EmMaj9), though its exact interpretation can vary slightly depending on the context.

The chord was first introduced by composer Monty Norman in the “James Bond Theme” for Dr. No (1962), arranged by John Barry, whose orchestration gave it its iconic swagger. …

First output

Grok produced the following LilyPond code

\version "2.22.0"

\score {
  \new Staff {
    \clef treble
    \key c \major % Default key, no sharps/flats; we'll specify accidentals manually
    \time 4/4
     <e g b dis' fis'>1 % EmMaj9 chord: E G B D# F#
  }
  \layout {}
  \midi {}
}

When compiled this gave the following music.

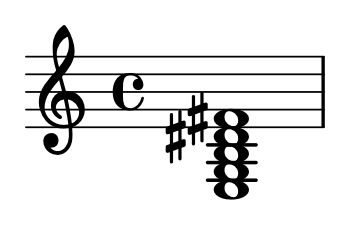
Grok also produce a MIDI file.

Second output

I wanted to move the chord up an octave for aesthetic reasons, putting the notes inside the staff. Grok complied, changing one line in the code, essentially adding an extra prime mark after each note.

<e' g' b' dis'' fis''>1 % EmMaj9 chord moved up an octave: E' G' B' D#'' F#''

This compiled to the following music.

Problems and prospects

Grok’s not perfect. In another experiment it produced code that wouldn’t compile. But when I told Grok that the code didn’t compile and asked it to try again, it worked.

I tried to remove the time signature, the C symbol. I asked Grok to remove it, and it did not. I asked Grok “How do you get LilyPond to produce music without a time signature?” and it told me two ways, neither of which worked.

I’ve used LilyPond occasionally for years, not to produce full sheets of music but to produce little fragments for blog posts. I’ve always found it a bit mysterious, in part because I jumped in and used it as needed without studying it systematically. There have been times when I thought about including some music notation in a blog post and didn’t want to go to the effort of using LilyPond (or rather the effort of debugging LilyPond if what I tried didn’t work). I may go to the effort more often now that I have a fairly reliable code generator.

Posts using LilyPond

Practical consequences of tokenization details

Posted on by John

I recently ran across the article Something weird is happening with LLMs and chess. One of the things it mentions is how the a minor variation in a prompt can have a large impact on the ability of an LLM to play chess.

One extremely strange thing I noticed was that if I gave a prompt like “1. e4 e5 2. ” (with a space at the end), the open models would play much, much worse than if I gave a prompt like “1 e4 e5 2.” (without a space) and let the model generate the space itself. Huh?

The author goes on to explain that tokenization probably explains the difference. The intent is to get the LLM to predict the next move, but the extra space confuses the model because it is tokenized differently than the spaces in front of the e’s. The trailing space is tokenized as an individual character, but the spaces in front of the e’s are tokenized with the e’s. I wrote about this a couple days ago in the post The difference between tokens and words.

For example, ChatGPT will tokenize “hello world” as [15339, 1917] and “world hello” as [14957, 24748]. The difference is that the first string is parsed as “hello” and ” world” while the latter is parsed as “world” and ” hello”. Note the spaces attached to the second word in each case.

The previous post was about how ChatGPT tokenizes individual Unicode characters. It mentions UTF-16, which is itself an example of how tokenization matters. The string “UTF-16” it will be represented by three tokens, one each for “UTF”, “-“, and “16”. But the string “UTF16” will be represented by two tokens, one for “UTF” and one for “16”. The string “UTF16” might be more likely to be interpreted as a unit, a Unicode encoding.

ChatGPT tokens and Unicode

Posted on by John

I mentioned in the previous post that not every Unicode character corresponds to a token in ChatGPT. Specifically I’m looking at gpt-3.5-turbo in tiktoken. There are 100,256 possible tokens and 155,063 Unicode characters, so the pigeon hole principle says not every character corresponds to a token.

I was curious about the relationship between tokens and Unicode so I looked into it a little further.

Low codes

The Unicode characters U+D800 through U+DFFF all map to a single token, 5809. This is because these are not really characters per se but “surrogates,” code points that are used in pairs to represent other code points [1]. They don’t make sense in isolation.

The character U+FFFD, the replacement character �, also corresponds to 5809. It’s also not a character per se but a way to signal that another character is not valid.

Aside from the surrogates and the replacement characters, every Unicode character in the BMP, characters up to U+FFFF, has a unique representation in tokens. However, most require two or three tokens. For example, the snowman character ☃ is represented by two tokens: [18107, 225].

Note that this discussion is about single characters, not words. As the previous post describes, many words are tokenized as entire words, or broken down into units larger than single characters.

High codes

The rest of the Unicode characters, those outside the BMP, all have unique token representations. Of these, 3,404 are represented by a single token, but the rest require 2, 3, or 4 tokens. The rocket emoji, U+1F680, for example, is represented by three tokens: [9468, 248, 222].

Rocket U+1F680 [9468, 248, 222]

[1] Unicode was originally limited to 16 bits, and UFT-16 represented each character with a 16-bit integer. When Unicode expanded to beyond 216 characters, UTF-16 used pairs of surrogates, one high surrogate and one low surrogate, to represent code points higher than U+FFFF.

The difference between tokens and words

Posted on by John

Large language models operate on tokens, not words, though tokens roughly correspond to words.

A list of words would not be practical. There is no definitive list of all English words, much less all words in all languages. Still, tokens correspond roughly to words, while being more flexible.

Words are typically turned into tokens using BPE (byte pair encoding). There are multiple implementations of this algorithm, giving different tokenizations. Here I use the tokenizer gpt-3.5-turbo used in GPT 3.5 and 4.

Hello world!

If we look at the sentence “Hello world!” we see that it turns into three tokens: 9906, 1917, and 0. These correspond to “Hello”, ” world”, and “!”.

In this example, each token corresponds to a word or punctuation mark, but there’s a little more going on. It is true that 0 is simply the token for the exclamation mark—we’ll explain why in a moment—it’s not quite true to say 9906 is the token for “hello” and 1917 is the token for “world”.

Many to one

In fact 1917 is the token for ” world”. Note the leading space. The token 1917 represents the word “world,” not capitalized and not at the beginning of a sentence. At the beginning of a sentence, “World” would be tokenized as 10343. So one word may correspond to several different tokens, depending on how the word is used.

One to many

It’s also true that a word may be broken into several tokens. Consider the sentence “Chuck Mangione plays the flugelhorn.” This sentence turns into 9 tokens, corresponding to

“Chuck”, “Mang”, “ione”, ” plays”, ” fl”, “ug”, “el”, “horn”, “.”

So while there is a token for the common name “Chuck”, there is no token for the less common name “Mangione”. And while there is a single token for ” trumpet” there is no token for the less common “flugelhorn.”

Characters

The tokenizer will break words down as far as necessary to represent them, down to single letters if need be.

Each ASCII character can be represented as a token, as well as many Unicode characters. (There are 100256 total tokens, but currently 154,998 Unicode characters, so not all Unicode characters can be represented as tokens.)

Update: The next post dives into the details of how Unicode characters are handled.

The first 31 ASCII characters are non-printable control characters, and ASCII character 32 is a space. So exclamation point is the first printable, non-space character, with ASCII code 33. The rest of the printable ASCII characters are tokenized as their ASCII value minus 33. So, for example, the letter A, ASCII 65, is tokenized as 65 − 33 = 32.

Tokenizing a dictionary

I ran every line of the american-english word list on my Linux box through the tokenizer, excluding possessives. There are 6,015 words that correspond to a single token, 37,012 that require two tokens, 26,283 that require three tokens, and so on. The maximum was a single word, netzahualcoyotl, that required 8 tokens.

The 6,015 words that correspond to a single token are the most common words in English, and so quite often a token does represent a word. (And maybe a little more, such as whether the word is capitalized.)

A simpler GELU activation function approximation

Posted on by John

The GELU (Gaussian Error Linear Units) activation function was proposed in [1]. This function is x Φ(x) where Φ is the CDF of a standard normal random variable. As you might guess, the motivation for the function involves probability. See [1] for details.

The GELU function is not too far from the more familiar ReLU, but it has advantages that we won’t get into here. In this post I wanted to look at approximations to the GELU function.

Since an implementation of Φ is not always available, the authors provide the following approximation:

\text{GELU(x)} \approx 0.5x\left(1 + \tanh\left(\sqrt{\frac{2}{\pi}} (x + 0.044715x^3) \right) \right)

I wrote about a similar but simpler approximation for Φ a while back, and multiplying by x gives the approximation

\text{GELU}(x) \approx 0.5x(1 + \tanh 0.8x)

The approximation in [1] is more accurate, though the difference between the exact values of GELU(x) and those of the simpler approximation are hard to see in a plot.

Since model weights are not usually needed to high precision, the simpler approximation may be indistinguishable in practice from the more accurate approximation.

Related posts

[1] Dan Hendrycks, Kevin Gimpel. Gaussian Error Linear Units (GELUs). Available on arXiv.

Spreading out words in space

Posted on by John

A common technique for memorizing numbers is to associate numbers with words. The Major mnemonic system does this by associating consonant sounds with each digit. You form words by inserting vowels as you please.

There are many possible encodings of numbers, but sometimes you want to pick a canonical word for each number, what’s commonly called a peg. Choosing pegs for the numbers 1 through 10, or even 1 through 100, is not difficult. Choosing pegs for a larger set of numbers becomes difficult for a couple reasons. First, it’s hard to think of words to fit some three-digit numbers. Second, you want your pegs to be dissimilar in order to avoid confusion.

Say for example you’ve chosen “syrup” for 049 and you need a peg for 350. You could use “molasses,” but that’s conceptually similar to “syrup.” If you use “Miles Davis” for 350 then there’s no confusion [1].

You could quantify how similar words are using cosine similarity between word embeddings.  A vector embedding associates a high-dimensional vector with each word in such a way that the geometry corresponds roughly with meaning. The famous example is that you might have, at least approximately,

queen = king − man + woman.

This gives you a way to define angles between words that ideally corresponds to conceptual similarity. Similar words would have a small angle between their vectors, while dissimilar words would have larger angles.

If you wanted to write a program to discover pegs for you, say using some corpus like ARPABet, you could have it choose alternatives that spread the words out conceptually. It’s debatable how practical this is, but it’s interesting nonetheless.

The angles you get would depend on the embedding you use. Here I’ll use the gensim code I used earlier in this post.

The angle between “syrup” and “molasses” is 69° but the angle between “syrup” and “miles” is 84°. The former is larger than I would have expected, but still significantly smaller than the latter. If you were using cosine similarity to suggest mnemonic pegs, hopefully the results would be directionally useful, choosing alternatives that minimize conceptual overlap.

As I said earlier, it’s debatable how useful this is. Mnemonics are very personal. A musician might be fine with using “trumpet” for 143 and “flugelhorn” for 857 because in his mind they’re completely different instruments, but someone else might think they’re too similar. And you might not want to use “Miles Davis” and “trumpet” as separate pegs, even though software will tell you that “miles” and “trumpet” are nearly orthogonal.

Related posts

[1] Here we’re following the convention that only the first three consonants in a word count. This makes it easier to think of pegs.

Mnemonic images with Grok 3

Posted on by John

The Major mnemonic system makes numbers easier to memorize by encoding them as words. Each digit corresponds to one or more consonant sounds, and you can fill in vowels as you wish.

In August 2022 I tried creating a few images using DALL-E 2. The results were disappointing and sometimes disturbing.

To illustrate the use of the Major system, I gave the example of memorizing a list of the US presidents by creating mental images associating each president with the number of their term as president. For example, Franklin Delano Roosevelt was the 32nd POTUS. You can encode 32 as “moon”, so you might imagine FDR looking up at the moon.

At the time, Grover Cleveland was the only US President to serve two non-consecutive terms, being both the 22nd and 24th president. I asked DALL-E to create an image of Grover the Muppet holding an onion (22) and a wiener dog (24). This was too much for DALL-E at the time. The image below was as close as I could get.

Blue dog holding cucumber dog?

When I asked Grok 3 for a similar image it did a much better job. To be fair, it initially put a different dog breed in Grover’s hand, but I asked it to change the dog to a dachshund and it performed admirably.

Grover holding an onion and a wiener dog

Related posts

Rich Sutton’s bitter lesson of AI

Posted on by John

This morning I read Alberto Romeo’s article Grok 3: Another Win For The Bitter Lesson. I wasn’t clear on what exactly the bitter lesson was, so I followed the link to Romeo’s previous article GPT-4: The Bitterer Lesson, which lead to Rich Sutton’s original article The Bitter Lesson.

Sutton opens his article by saying

The biggest lesson that can be read from 70 years of AI research is that general methods that leverage computation are ultimately the most effective, and by a large margin.

Clear enough, except you have to read further to get the “compared to what.” I asked Grok 3 to read the article and tell me exactly what the bitter lesson is. It begins with this explanation:

The “Bitter Lesson” is the principle that, in the field of artificial intelligence, the most effective and lasting progress has historically come from methods that rely on leveraging ever-increasing computational power rather than depending on human ingenuity to craft domain-specific knowledge or shortcuts. …

and concludes with the following pithy summary of its summary:

In essence, the Bitter Lesson is: computation trumps human-crafted specialization in AI, and embracing this, though humbling, is key to future success.

Sutton supports his thesis with examples from chess, go, speech recognition, and computer vision.

In some sense this is the triumph of statistics over logic. All else being equal, collecting enormous amounts of data and doing statistical analysis (i.e. training an AI model) will beat out rule-based systems. But of course all else is often not equal. Logic is often the way to go, even on big problems.

When you do know whats going on and can write down a (potentially large) set of logical requirements, exploiting that knowledge via techniques like SAT solvers and SMT is the way to go. See, for example, Wayne’s article on constraint programming. But if you want to build the Everything Machine, building software that wants to be all things to all people, statistics is the way to go.

Sometimes you have a modest amount of relevant data, and you don’t have 200,000 Nvidia H100 GPUs. In that case you’re much better off with classical statistics than AI. Classical models are more robust and easier to interpret. They are also not subject to hastily written AI regulation.

Putting a face on a faceless account

Posted on by John

I’ve been playing around with Grok today, logging into some of my X accounts and trying out the prompt “Draw an image of me based on my posts.” [1] In most cases Grok returned a graphic, but sometimes it would respond with a text description. In the latter case asking for a photorealistic image made it produce a graphic.

Here’s what I get for @AlgebraFact:

The icons for all my accounts are cerulean blue dots with a symbol in the middle. Usually Grok picks up on the color, as above. With @AnalysisFact, it dropped a big blue piece of a circle on the image.

For @UnixToolTip it kept the & from the &> in the icon. Generative AI typically does weird things with text in images, but it picked up “awk” correctly.

Here’s @ProbFact. Grok seems to think it’s a baseball statistics account.

Last but not least, here’s @DataSciFact.

I wrote a popular post about how to put Santa hats on top of symbols in LaTeX, and that post must have had an outsided influence on the image Grok created.

[1] Apparently if you’re logging into account A and ask it to draw B, the image will be heavily influence by A‘s posts, not B‘s. You have to log into B and ask in the first person.

Golden hospital gowns

Posted on by John

Here’s something I posted on X a couple days ago:

There’s no direct connection between AI and cryptocurrency, but they have a similar vibe.

They both leave you wondering whether the emperor is sumptuously clothed, naked, or a mix of both.

Maybe he’s wearing a hospital gown with gold threads.

In case you’re unfamiliar with the story, this is an allusion to The Emperor’s New Clothes, one of the most important stories in literature.

I propose golden hospital gown as a metaphor for things that are a fascinating mixture of good and bad, things that have large numbers of haters and fanboys, both with valid points. There’s continual improvement and a lot work to be done sorting out what works well and what does not.

I tried to get Grok to create an image of what I had in mind by a golden hospital gown. The results were not what I wanted, but passable, which is kinda the point of the comment above. It’s amazing that AI can produce anything remotely resembling a desired image starting from a text description. But there is a very strong temptation to settle for mediocre and vaguely creepy images that aren’t what we really want.

Man in a yellow hospital gown with hairy back and legs exposed

Related posts