Bigger animals have more cells than smaller animals. More cells means more cellular metabolism and so more heat produced. How does the amount of heat an animal produces vary with its size? We clearly expect it to go up with size, but does it increase in proportion to volume? Surface area? Something in between?
A first guess would be that metabolism (equivalently, heat produced) goes up in proportion to volume. If cells are all roughly the same size, then number of cells increases proportionately with volume. But heat is dissipated through the surface. Surface area increases in proportion to the square of length but volume increases in proportion to the cube of length. That means the ratio of surface area to volume decreases as overall size increases. The surface area to volume ratio for an elephant is much smaller than it is for a mouse. If an elephant’s metabolism per unit volume were the same as that of a mouse, the elephant’s skin would burn up.
So metabolism cannot be proportional to volume. What about surface area? Here we get into variety and controversy. Many people assume metabolism is proportional to surface area based on the argument above. This idea was first proposed by Max Rubner in 1883. Others emphasize data that supports the theory that suggests metabolism is proportional to surface area.
In the 1930s, Max Kleiber proposed that metabolism increases according to body mass raised to the power 3/4. (I’ve been a little sloppy here using body mass and volume interchangeably. Body mass is more accurate, though to first approximation animals have uniform density.) If metabolism were proportional to volume, the exponent would be 1. If it were proportional to surface area, the exponent would be 2/3. But Kleiber’s law says it’s somewhere in between, namely 3/4. The image below comes from a paper by Kleiber from 1947.
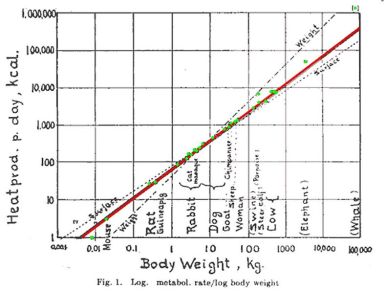
The graph shows that on a log-log plot, the metabolism rate versus body mass for a large variety of animals has slope approximately 3/4.
So why the exponent 3/4? There is a theoretical explanation called the metabolic scaling theory proposed by Geoffrey West, Brian Enquist, and James Brown. Metabolic scaling theory says that circulatory systems and other networks are fractal-like because this is the most efficient way to serve an animal’s physiological needs. To quote Enquist:
Although living things occupy a three-dimensional space, their internal physiology and anatomy operate as if they were four-dimensional. … Fractal geometry has literally given life an added dimension.
The fractal theory would explain the power law exponent 3/4 simply: it’s the ratio of the volume dimension to the fractal dimension. However, as I suggested earlier, this theory is controversial. Some biologists dispute Kleiber’s law. Others accept Kleiber’s law as an empirical observation but dispute the theoretical explanation of West, Enquist, and Brown.
To read more about metabolism and power laws, see chapter 17 of Complexity: A Guided Tour.

Thank you for the interesting post. You’ve motivated me to put ‘Complexity’ on pre-order (it isn’t yet out in the UK). If I could get hold of some of the data, it would certainly give some purpose to the ‘draw a line of best fit’ lesson.
The “power law” strikes me as not very meaningful.
Each animal is a different design. An elephant is not just a very big mouse. The design is different, and the differences are likely tied to heat control.
Thinking about elephants in warm climates – there are two aspects to the design of an elephant that increase surface area (and allow for heat loss). First, elephants seem generally to have rather large ears, and the ears could be very effective heat radiators (what does a thermal picture of an elephant look like?). Second, all animals have an interior surface area – the lungs. Does the surface area of the lungs track the product of metabolic rate and animal weight? Is the respiratory system designed to conserve or expel heat? My guess is we get different answers for different animals.
How would an ice-age mastodon compare to a modern tropical elephant? Would the metabolic rates differ? Would the large ears disappear? Would the design of the respiratory system change to conserve heat?
Can evolution force relatively rapid change in metabolic rates, or is this design aspect only very slow to change? The metabolic rates of large tropical and polar dinosaurs would be interesting to know – but that data will be hard to obtain.
Yes, as a rough average, the metabolic rates of large animals have to be lower than small animals – but individual differences in design (driven by successful ecological niches) are going to move the data points around quite a lot. Trying to derive a single formula is a nearly meaningless exercise.
There is perhaps an interesting bit of data to be derived from metabolic rates. Assuming that changes to cell chemistry are slow on an evolutionary time scale (a big assumption that needs testing), then similar metabolic rates might provide a measure of genetic distance between species.
I’m fascinating by this stuff and have found biometrician Steven Vogel’s works on comparative biomechanics most approachable and interesting. He began with LIVE IN MOVING FLUIDS and went on from there. I have bought copies of his VITAL CIRCUITS for 5 physicians. He has a textbook called COMPARATIVE BIOMECHANICS which discusses exactly this point. I he’d disagree that “Trying to derive a single formula is a nearly meaningless exercise” because from such attempts, much can be learned about biology-in-the-large, even if a particular species might be odd.
I’m about to launch into his CAT PAWS AND CATAPULTS, BTW.
This reminds me of On Being the Right Size, by J.B.S. Haldane, written in 1928, and online here: http://irl.cs.ucla.edu/papers/right-size.html
Have you read it?
BTW, Vogel’s COMPARATIVE cites a 1961 Kleiber, THE FIRE OF LIFE, AN INTRODUCTION TO ANIMAL ENERGETICS, Wiley, on his page 45. Chapter 3 of COMPARATIVE is devoted to “Size and Scale”.
Oh, and to “Second, all animals have an interior surface area – the lungs. Does the surface area of the lungs track the product of metabolic rate and animal weight?”, strictly speaking, lungs are part of the OUTSIDE surface area, as is the alimentary canal.
Sorry posting from different computers and cookie sets: ekzept == Jan Theodore Galkowski
And it’s all wrong! Geoffrey West and the clowns at Santa’s Fey Institute have been able to perpetuate bunk for over a decade now because, as formulated, it has no consequence and can make no predictions. I recommend the essay at the site Theoretical Biology and Medical Modelling entitled “The terrestrial origins of metabolism and life – by the numbers” for a treatment of allometric scaling that clearly suggests West, Brown and Enquist are way off the mark. This treatment of the issue generates numerous, testable deductive inferences. The bell has wrung. It’s time for the old guard to leave the stage and turn the future over to the young.
This helped me for my ecology exam. Thanks!
Preston L. Bannister :
You are right, each design solves problems in the organisms environment. However, this article talks about metabolism as the generation, the output, of heat. Not how it is released into the environment, but how much builds up over time for a given mass.