Body Roundness Index (BRI) is a proposed replacement for Body Mass Index (BMI) [1]. Some studies have found that BRI is a better measure of obesity and a more effective predictor of some of the things BMI is supposed to predict [2].
BMI is based on body mass and height, and so it cannot distinguish a body builder and an obese man if both have the same height and weight. BRI looks at body shape more than body mass.
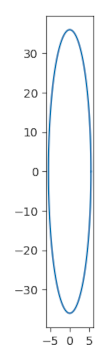
The basic idea behind Body Roundness Index is to draw an ellipse based on a person’s body and report how close that ellipse is to being a circle. The more a person looks like a circle, higher his BRI. The formula for BRI is
BRI = 364.2 − 365.5 e
where e is the eccentricity of the ellipse.
Now what is this ellipse we’ve been talking about? It’s roughly an ellipse whose major axis runs from head to toe and whose minor axis runs across the person’s width.
There are a couple simplifications here.
- You don’t actually measure how wide someone is. You measure the circumference of their waist and find the diameter of a circle with that circumference.
- You don’t actually measure how high their waist is [3]. You assume their waist is at exactly half their height.
It’s conventional to describe an ellipse in terms of its semi-major axis a and semi-minor axis b. For a circle, a = b = radius. But in general an ellipse doesn’t have a single radius and a > b. You could think of a and b as being the maximum and minimum radii.
So to fit an ellipse to our idealized model of a person, the major axis, 2a, equals the person’s height.
a = h/2
The minor axis b is the radius of a circle of circumference c where c is the circumference of the person’s waist (or hips [3]).
b = c / 2π
As explained here, eccentricity is computed from a and b by
As an example, consider a man who is 6 foot (72 inches) tall and has a 34 inch waist. Then
a = 36
b = 17/π = 5.4112
e = √(1 − b²/a²) = 0.9886
BRI = 364.2 − 365.5 e = 2.8526
Note that the man’s weight doesn’t enter the calculation. He could be a slim guy weighing 180 pounds or a beefier guy weighing 250 pounds as long as he has a 34 inch waist. In the latter case, the extra mass is upper body muscle and not around his waist.
Related posts
[1] Diana M. Thomas et al. Relationships Between Body Roundness with Body Fat and Visceral Adipose Tissue Emerging from a New Geometrical Model. Obesity (2013) 21, 2264–2271. doi:10.1002/oby.20408.
[2] Researchers argue over which number to reduce a person to: BMI, BRI, or some other measure. They implicitly agree that a person must be reduced to a number; they just disagree on which number.
[3] Or waist. There are two versions of BRI, one based on waist circumference and one based on hip circumference.