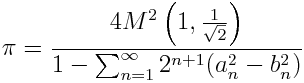This post gives an algorithm based on the arithmetic-geometric mean that rapidly converges to pi. I’ll use it to illustrate multiple precision arithmetic using Python’s mpmath module.

Given two non-negative numbers a and b, their arithmetic mean is (a + b)/2 and their geometric mean is √(ab). Suppose you start with two non-negative numbers and take their arithmetic mean and geometric mean. Then take the arithmetic and geometric mean of the results. Keep doing this repeatedly, and the result converges to what is called the arithmetic-geometric mean (AGM).

There is a formula for calculating pi based on the AGM that goes back to Gauss.

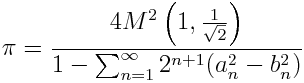
Here M(a, b) is the AGM of a and b, and a_n and b_n are the values after n steps of the iteration.

The process defining the AGM converges quickly, and so the formula is practical for computing pi. I found it in a paper from 1988, and at that time the formula had been used to compute pi to over 29 million decimal places. In the code below, we compute pi to 997 decimal places in only 10 iterations.

from mpmath import mp, sqrt, mpf, pi, log10, fabs

# carry out calculations to 1000 decimal places
decimal_places = 1000
mp.dps = decimal_places
epsilon = 1/mpf(10**decimal_places)

# set a = 1 and b = 1/sqrt(2) as multi-precision numbers
a = mpf(1)
b = 1/sqrt(mpf(2))

diff = a - b
series = mpf(0)

n = 0
while diff > epsilon:
    n += 1
    arith = (a + b)/2
    geom = sqrt(a*b)
    a, b = arith, geom
    series += 2**(n+1) * (a*a - b*b)
    diff = a - b

# a and b have converged to the AGM
my_pi = 4*a*a/(1 - series)

error = fabs(pi - my_pi)
decimal_places = int(-log10(error))

print "Number of steps used: %d" % n
print "Number of correct decimal places: %d" % decimal_places

The code can be used to calculate pi out further. The number of correct decimal places roughly doubles with each iteration. For example, computing pi to 10,000 places takes only 3 more iterations.

More posts on computing pi

• Algorithm for world record pi calculations
• Ramanujan series for pi