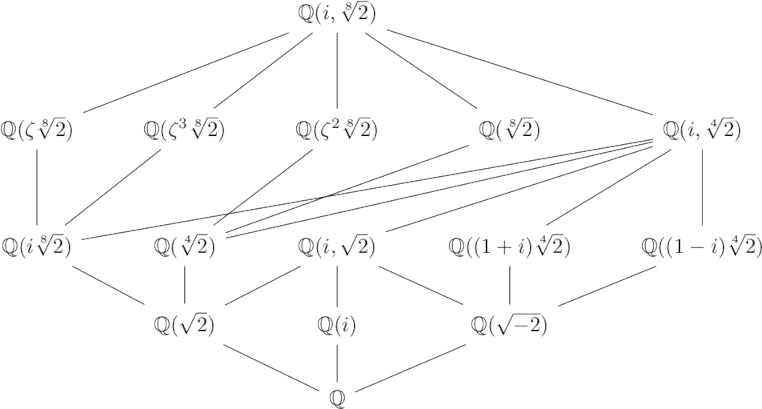
Courant & Hilbert is a classic applied math textbook, still in print nearly a century after the first edition came out. The actual title of the book is Methods of Mathematical Physics, but everyone calls it Courant & Hilbert after the authors, Richard Courant and David Hilbert. I was surprised to find out recently that this was once a banned book. How could there be anything controversial about a math book? It doesn’t get into any controversial applications of math; it applies math to physics problems, but doesn’t apply the physics to anything in particular.
The book was first published in Germany in 1924 under the title Methoden der mathematischen Physik. Courant says in the preface
… I had been forced to leave Germany and was fortunate and grateful to be given the opportunities open in the United States. During the Second World War the German book became unavailable and was even suppressed by the National Socialist rulers of Germany. The survival of the book was secured when the United States Government seized the copyright and licensed a reprint issued by Interscience Publishers.
Courant’s language is remarkably restrained under the circumstances.
I wondered why the book was banned. Was Courant Jewish? I’d never considered this before, because I couldn’t care less about the ethnicity of authors. Jew or Greek, bond or free, male or female, I just care about their content. The Nazis, however, did care. According to his Wikipedia biography, Courant fled Germany not because of his Jewish ancestry but because of his affiliation with the wrong political party.
***
I never had Courant & Hilbert as a textbook, but I was familiar with it as a student. I vaguely remember that the library copy was in high demand and that I considered buying a copy, though it was too expensive for my means at the time. I recently bought a copy now that the book is cheaper and my means have improved.
I covered most of the material in Courant & Hilbert in graduate school, albeit in a more abstract form. As I mentioned the other day, my education was somewhat top-down; I learned about things first in an abstract setting and got down to particulars later, moving from soft analysis to hard analysis.
One quick anecdote along these lines. I read somewhere that David Hilbert was at a conference where someone referred to a Hilbert space and he asked the speaker what such a thing was. Hilbert’s work had motivated the definition of a Hilbert space, but Mr. Hilbert thought in more concrete terms.