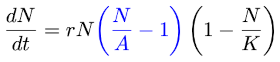Programming

Pioneering work is ugly

Posted on by John

“A mathematician’s reputation rests on the number of bad proofs he has given. (Pioneer work is clumsy.)” — A. S. Besicovitch

I’m sure I’ve written about this quote somewhere, but I can’t find where. The quote comes from A Mathematician’s Miscellany by J. E. Littlewood, citing Besicovitch.

I’ve more often seen the quote concluding with “Pioneering work is ugly.” Maybe that’s what Besicovitch actually said, but I suspect it came from someone misremembering/improving Littlewood’s citation. Since the words are in parentheses, perhaps Besicovitch didn’t say them at all but Littlewood added them as commentary.

One way of interpreting the quote is to say it takes more creativity to produce a rough draft than to edit it.

The quote came to mind when I was talking to a colleague about the value of ugly code, code that is either used once or that serves as a prototype for something more lasting.

This is nearly the opposite of the attitude I had as a software developer and as a software team manager. But it all depends on context. Software techniques need to scale down as well as scale up. It doesn’t make sense to apply the same formality to disposable code and to enterprise software.

Yes, supposedly disposable code can become permanent. And as soon as someone realizes that disposable code isn’t being disposed of it should be tidied up. But to write every little one-liner as if it is going to be preserved for posterity is absurd.

Naming Awk

Posted on by John

The Awk programming language was named after the initials of its creators. In the preface to a book that just came out, The AWK Programming Language, Second Edition, the authors give a little background on this.

Naming a language after its creators shows a certain paucity of imagination. In our defense, we didn’t have a better idea, and by coincidence, at some point in the process we were in three adjacent offices in the order Aho, Weinberger, and Kernighan.

By the way, here’s a nice line from near the end of the book.

Realistically, if you’re going to learn only one programming language, Python is the one. But for small programs typed at the command line, Awk is hard to beat.

A small programming language

Posted on by John

Paul Graham said “Programming languages teach you not to want what they don’t provide.” He meant that as a negative: programmers using less expressive languages don’t know what they’re missing. But you could also take that as a positive: using a simple language can teach you that you don’t need features you thought you needed.

Awk

I read the original awk book recently, published in 1988. It’s a small book for a small language. The language has grown since 1988, especially the Gnu implementation gawk, and yet from the beginning the language had a useful set of features. Most of what has been added since then is of no use to me.

How I use awk

It has been years since I’ve written an awk program that is more than one line. If something would require more than one line of awk, I probably wouldn’t use awk. I’m not morally opposed to writing longer awk programs, but awk’s sweet spot is very short programs typed at the command line.

At one point when I was saying how I like little awk programs, someone suggested I use Perl one-liners instead because then I’d have access to Perl’s much richer set of features, in particular Perl regular expressions. Along those lines, see these notes on how to write Perl one-liners to mimic sed, grep, and awk.

But when I was reading the awk book I thought about how I rarely need the the features awk doesn’t have, not for the way I use awk. If I were writing a large program, not only would I want more features, I’d want a different language.

Now my response to the suggestion to use Perl one-liners would be that the simplicity of awk helps me focus by limiting my options. Awk is a jig. In Paul Graham’s terms, awk teaches me not to want what it doesn’t provide.

Regular expressions

At first I wished awk were more expressive is in its regular expression implementation. But awk’s minimal regex syntax is consistent with the aesthetic of the rest of the language. Awk has managed to maintain its elegant simplicity by resisting calls to add minor conveniences that would complicate the language. The maintainers are right not to add the regex features I miss.

Awk does not support, for example, \d for digits. You have to type [0-9] instead. In exchange for such minor inconveniences you get a simple but adequate regular expression implementation that you could learn quickly. See notes on awk’s regex features here.

The awk book describes regular expressions in four leisurely pages. Perl regular expressions are an order of magnitude more complex, but not an order of magnitude more useful.

 

Productive constraints

Posted on by John

This post will discuss two scripting languages, but that’s not what the post is really about. It’s really about expressiveness and (or versus) productivity.

***

I was excited to discover the awk programming language sometime in college because I had not used a scripting language before. Compared to C, awk was high-level luxury.

Then a few weeks later someone said “Have you seen Perl? It can do everything awk can do and a lot more.” So I learned Perl. Was that or a good idea or a bad idea? I’ve been wondering about that for years.

Awk versus Perl is a metaphor for a lot of other decisions.

***

Awk is a very small language, best suited for working with tabular data files. Awk implicitly loops over a file, repeating some code on every line of a file. This makes it possible to write very short programs, programs so short that they can be typed at the command line, for doing common tasks. I am continually impressed by bits of awk code I see here and there, where someone has found a short, elegant solution to a problem.

Because awk is small and specialized, it is also efficient at solving the problems it is designed to solve. The previous post gives an example.

The flip side of awk being small and specialized is that it can be awkward to use for problems that deviate from its sweet spot.

***

Perl is a very expressive programming language and is suitable for a larger class of problems than awk is. Awk was one of the influences in the design of Perl, and you can program in an awk-like subset of Perl. So why not give yourself more options and write Perl instead?

Expressiveness is mostly good. Nobody is forcing you to use any features you don’t want to use and it’s nice to have options. But expressiveness isn’t a free option. I’ll mention three costs.

  1. You might accidentally use a feature that you don’t intend to use, and rather than getting an error message you get unexpected behavior. This is not a hypothetical risk but a common experience.
  2. If you have more options, so does everyone writing code that you might need to debug or maintain. “Expressiveness for me but not for thee.”
  3. More options means more time spent debating options. Having too many options dissipates your energy.

***

You can mitigate #1 by turning on warnings available in later versions of Perl. And you can mitigate #2 and #3 by deciding which language features you (or your team) will use and which features you will avoid.

But if you use a less expressive language, these decisions have been made for you. No need to decide on and enforce rules on features to shun. Avoiding decision fatigue is great, if you can live with the decisions that have been made for you.

The Python community has flourished in part because the people who don’t like the language’s design choices would rather live with those choices than leave these issues permanently unsettled.

***

Bruce Lee famously said “I fear not the man who has practiced 10,000 kicks once, but I fear the man who has practiced one kick 10,000 times.” You could apply that aphorism by choosing to master a small language like awk, learning not just its syntax but its idioms, and learning it so well that you never need to consult documentation.

Some people have done this, mastering awk and a few other utilities. They write brief scripts that do tasks that seem like they would require far more code. I look at these scripts expecting to see utilities or features that I didn’t know about, but usually these people have combined familiar pieces in a clever way.

***

Some people like to write haiku and some free verse. Hedgehogs and foxes. Scheme and Common Lisp. Birds and Frogs. Awk and Perl. So the optimal size of your toolbox is to some extent a matter of personality. But it’s also a matter of tasks and circumstances. There are no solutions, only trade-offs.

Software and the Allee effect

Posted on by John

The Allee effect is named after Warder Clyde Allee who added a term to the famous logistic equation. His added term is highlighted in blue.

\frac{dN}{dt} = r N {\color{red}\left( \frac{N}{A} - 1 \right)} \left( 1 - \frac{N}{K} \right)

Here N is the population of a species over time, r is the intrinsic rate of increase, K is the carrying capacity, and A is the critical point.

If you remove Allee’s term, you get an equation saying that the rate of growth of a population is proportional to the current population size, and so growth starts out exponential, and a term (1 – N/K), which says growth slows down as the population approaches its carrying capacity.

Allee’s term (N/A – 1) says that the rate of growth becomes negative when the population falls below some threshold A. When there are too few individuals, survival becomes more difficult.

Software metaphor

I thought of the Allee effect as a metaphor for software technology after writing my previous post. In general, problems become easier to solve over time. Software development may become harder because the problems developers solve are changing, but solving old problems typically gets easier. Algorithms improve and get wrapped up for convenience. There’s something like logistic growth where tasks get easier to solve, but improvement slows down over time.

If a problem is specialized, it can run into something like the Allee effect. It becomes harder over time because fewer people are interested in it. Software isn’t maintained as fast as it degrades. Fewer people have experience with it. It’s harder to be a COBOL programmer, for example, than it used to be. But this can also apply to much more current problems. A problem that was hot five years ago can be harder to solve now than it was then, for reasons the previous post discusses.

Branch cuts for elementary functions

Posted on by John

As far as I know, all contemporary math libraries use the same branch cuts when extending elementary functions to the complex plane. It seems that the current conventions date back to Kahan’s paper [1]. I imagine to some extent he codified existing practice, but he also settled some issues, particularly regarding floating point implementation.

I’ve verified that the following branch cuts are used by Mathematica, Common Lisp, and SciPy. If you know of any software that follows other conventions, please let me know in a comment.

The conventional branch cuts are as follows.

  • sqrt: [−∞, 0)
  • log: [−∞, 0]
  • arcsin: [−∞, −1] and [1, ∞]
  • arccos: [−∞, −1] and [1, ∞]
  • arctan: [−∞i, −i] and [i, ∞i]
  • arcsinh: [−∞i, −i] and [i, ∞i]
  • arccosh: [−∞, 1]
  • arctanh: [−∞, -1] and [1, ∞]

Related posts

[1] W. Kahan. Branch Cuts for Complex Elementary Functions or Much Ado About Nothing’s Sign Bit. The State of the Art in Numerical Analysis. Clarendon Preess (1987).

Code katas taken more literally

Posted on by John

Karate class

Code katas are programming exercises intended to develop programming skills, analogous to the way katas develop martial art skills.

But literal katas are choreographed. They are rituals rather than problem-solving exercises. There may be an element of problem solving, such as figuring how to better execute the prescribed movements, but katas are rehearsal rather than improvisation.

CodeKata.com brings up the analogy to musical practice in the opening paragraph of the home page. But musical practice is also more ritual than problem-solving, at least for classical music. A musician might go through major and minor scales in all 12 keys, then maybe a chromatic scale over the range of the instrument, then two different whole-tone scales, etc.

A code kata would be more like a jazz musician improvising a different melody to the same chord changes every day. (Richie Cole would show off by improvising over the chord changes to Cherokee in all twelve keys. I don’t know whether this was a ritual for him or something he would pull out for performances.)

This brings up a couple questions. What would a more literal analog of katas look like for programming? Would these be useful?

I could imagine someone going through a prescribed sequence of keystrokes that exercise a set of software features that they wanted to keep top of mind, sorta like practicing penmanship by writing out a pangram.

This is admittedly a kind of an odd idea. It makes sense that the kinds of exercises programmers are interested in require problem solving rather than recall. But maybe it would appeal to some people.

***

Image “karate training” by Genista is licensed under CC BY-SA 2.0 .

Visualizing C operator precedence

Posted on by John

Here’s an idea for visualizing C operator precedence. You snake your way through the diagram starting from left to right.

Operators at the same precedence level are on the same horizontal level.

Following the arrows for changing directions, you move from left-to-right through the operators that associate left-to-right and you move right-to-left through the operators that associate right-to-left.

Although this diagram is specifically for C, many languages follow the same precedence with minor exceptions. For example, all operators that Perl shares with C follow the same precedence as C.

visualization of C operator precedence

Related posts

Pareto and Pandas

Posted on by John

This post muses about what it means to learn a software library. I’ll use Pandas as an example, but the post isn’t just about Pandas.

Suppose you say “I want to learn Pandas.” That implicitly assumes Pandas one thing, and in a sense it is. In another sense Pandas is hundreds of things.

At the top level, the pandas module (version 1.2.0) has 142 things inside.

    >>> import pandas as pd
    >>> len(dir(pd))
    142

The two most important things inside are the Series and DataFrame objects. They each in turn contain hundreds of things.

    >>> len(dir(pd.Series))
    434
    >>> len(dir(pd.DataFrame))
    441

That’s evidence Pandas’ diversity. But here’s evidence of it’s unity: most of the things inside these two objects have the same names.

    >>> s = set(dir(pd.Series))
    >>> d = set(dir(pd.DataFrame))
    >>> len(s.union(d))
    491
    >>> len(s - d)
    50
    >>> len(d - s)
    57

Pandas kinda has a fractal dimension, having both complexity and unity. The best way to think about it is not as one monolithic thing, or as hundreds of isolated things. It’s a coherent, but not perfectly coherent, collection of related things. This is true of all software libraries. Pandas is more coherent than most libraries because it was initially the product of one mind, that of Wes McKinney.

This has a couple implications for what it means to “learn Pandas.” Because Pandas is big, you have to explore it strategically, not exhaustively. And because Pandas is coherent, part of what it means to learn Pandas is to develop a feel for the way Pandas does things.

No one is going to learn Pandas by studying every object, every method on every object, and every argument to every method on every object. It’s too big. That’s also unnecessary.

There’s probably something like a Pareto distribution on the usefulness of features. The most commonly used features are used far, far more often than the most obscure features.

It would be interesting to do some kind of survey to see which features are actually used and how often. But I don’t think that’s practical. The easiest thing to do would be to find some large code base that heavily uses Pandas. But that’s not typical of how Pandas is used. Probably most lines of code using Pandas are scattered over millions of small scripts, much of it not in production code.

A well-designed library makes it possible to make good guesses about functionality you haven’t used. You learn the gestalt of the library. You can always look up API documentation as needed, but you can’t develop an intuition for a library just-in-time.

“Learn Pandas” is a daunting goal, and maybe an impossible goal if by “learn” you mean explore exhaustively. But “learn how to do my common tasks quickly in Pandas” and “develop a feel for how to do things in Pandas” are much smaller tasks.

Related posts

Expressiveness

Posted on by John

Programmers like highly expressive programming languages, but programming managers do not. I wrote about this on Twitter a few months ago.

Q: Why do people like Lisp so much?

A: Because Lisp is so expressive.

Q: Why don’t teams use Lisp much?

A: Because Lisp is so expressive.

Q: Why do programmers complain about Java?

A: Because it’s not that expressive.

Q: Why do businesses use Java?

A: Because it’s not that expressive.

A highly expressive programming language offers lots of options. This can be a good thing. It makes programming more fun, and it can lead to better code. But it can also lead to more idiosyncratic code.

A large programming language like Perl allows developers to carve out language subsets that hardly overlap. A team member has to learn not only the parts of the language he understands and wants to use, but also all the parts that his colleagues might use. And those parts that he might accidentally use.

While Perl has maximal syntax, Lisp has minimal syntax. But Lisp is also very expressive, albeit in a different way. Lisp makes it very easy to extend the language via macros. While Perl is a big language, Lisp is an extensible language. This can also lead to each programmer practically having their own language.

With great expressiveness comes great responsibility. A team using a highly expressive language needs to develop conventions for how the language will be used in order to avoid fracturing into multiple de facto languages.

But what if you’re a team of one? Now you don’t need to be as concerned how other people use your language. You still may need to care somewhat. You want to be able to grab sample code online, and you may want to share code or ask others for help. It pays not to be entirely idiosyncratic, though you’re free to wander further from the mainstream.

Even when you’re working in a team, you still may have code that only you use. If your team is producing C# code, and you secretively use a Perl script to help you find things in the code, no one needs to know. On the other hand, there’s a tendency for personal code to become production code, and so personal tools in a team environment are tricky.

But if you’re truly working by yourself, you have great freedom in your choice of tools. This can take a long time to sort out when you leave a team environment to strike out on your own. You may labor under your previous restrictions for a while before realizing they’re no longer necessary. At the same time, you may choose to stick to your old tools, not because they’re optimal for your new situation, but because it’s not worth the effort to retool.

Related posts

(Regarding the last link, think myth as in Joseph Campbell, not myth as in Myth Busters.)