Randomized clinical trials essentially flip a coin to assign patients to treatment arms. Outcome-adaptive randomization “bends” the coin to favor what appears to be the better treatment at the time each randomized assignment is made. The method aims to treat more patients in the trial effectively, and on average it succeeds.
However, looking only at the average number of patients assigned to each treatment arm conceals the fact that the number of patients assigned to each arm can be surprisingly variable compared to equal randomization.
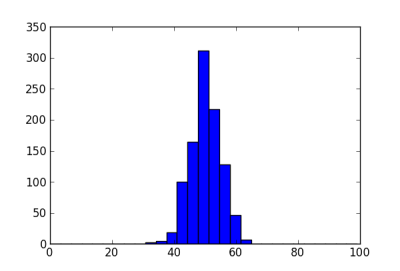
Suppose we have 100 patients to enroll in a clinical trial. If we assign each patient to a treatment arm with probability 1/2, there will be about 50 patients on each treatment. The following histogram shows the number of patients assigned to the first treatment arm in 1000 simulations. The standard deviation is about 5.
Next we let the randomization probability vary. Suppose the true probability of response is 50% on one arm and 70% on the other. We model the probability of response on each arm as a beta distribution, starting from a uniform prior. We randomize to an arm with probability equal to the posterior probability that that arm has higher response. The histogram below shows the number of patients assigned to the better treatment in 1000 simulations.
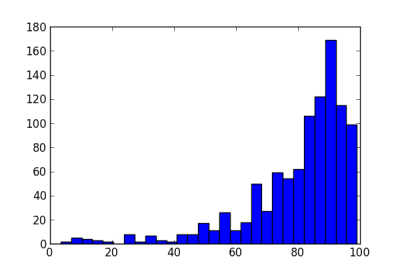
The standard deviation in the number of patients is now about 17. Note that while most trials assign 50 or more patients to the better treatment, some trials in this simulation put less than 20 patients on this treatment. Not only will these trials treat patients less effectively, they will also have low statistical power (as will the trials that put nearly all the patients on the better arm).
The reason for this volatility is that the method can easily be mislead by early outcomes. With one or two early failures on an arm, the method could assign more patients to the other arm and not give the first arm a chance to redeem itself.
Because of this dynamic, various methods have been proposed to add “ballast” to adaptive randomization. See a comparison of three such methods here. These methods reduce the volatility in adaptive randomization, but do not eliminate it. For example, the following histogram shows the effect of adding a burn-in period to the example above, randomizing the first 20 patients equally.
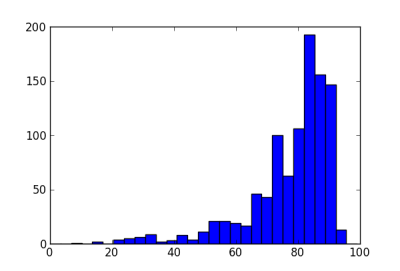
The standard deviation is now 13.8, less than without the burn-in period, but still large compared to a standard deviation of 5 for equal randomization.
Another approach is to transform the randomization probability. If we use an exponential tuning parameter of 0.5, the sample standard deviation of the number of patients on the better arm is essentially the same, 13.4. If we combine a burn-in period of 20 and an exponential parameter of 0.5, the sample standard deviation is 11.7, still more than twice that of equal randomization.

This topic is extremely relevant for online marketing right now in the spaces of A/B testing and ad placement optimization (where people call this multiarm bandit). There’s another criticism which I read which focuses mainly on how it will show statistical significance slower. But your post points out a scarier downside.
My complaint has always been that this sort of experimentation assumes independence of response with time; which is often not true. If you are changing your p of assignment over time and there is a period where response is more likely then if p is leaning in a particular direction at that time you will end up with misleading results.
Bandit testing would work better in advertising than in medicine. It’s OK for an ad server to know what assignments are coming up, but randomization reduces the potential bias of human researchers. But because bandits are optimal under certain assumptions, it’s reasonable to wonder whether they would perform well when those assumptions are violated.
Adaptive randomization may be more robust against changes to response over time. In the context of medicine, we call this “population drift.” Here is a tech report that explores adaptive randomization and population drift.
Adaptive randomization (AR) has been criticized lately for being less powerful than equal randomization (ER). For two arms, it seems that AR is less powerful than ER unless the response probabilities on the two arms are extremely different, something that rarely happens in practice.
For three or more arms, the situation is less clear. It’s plausible that the ability to drop poorly performing arms could make AR more powerful than ER. In simulations that I’ve run, it seems that the benefit of AR comes from being able to drop an arm, not from changing the randomization probability. In the scenarios I’ve looked at, it’s best to randomize equally to an inferior arm until you drop it, rather than to gradually starve it by lowering its assignment probability.
Am I missing something here, or is part of the problem that we’re trying to do two incompatible things at once? The point of a clinical trial is to determine whether a given treatment is effective, and (if you’re lucky) to quantify that effect. In the long run, it’s more valuable to get the best possible information out of the trial than it is to treat the trial participants effectively. Trial participants sign waivers that assert they understand this, and are OK with it.
Thank you so much John. That’s really insightful (note for those who don’t follow the link is it’s a paper on exactly the topic I was asking about written by John).
Follow up question: while AR still has better expected value under population drift wouldn’t drift increase the variance issue discussed here? Particularly for rising tide.
Although, as I ask that question I suspect the answer is: yes, but not by much. It appears from your research that even large drift has only a subtle effect on results.
When you say that “[…] it seems that AR is less powerful than ER […]” what do you mean by “less powerful”? Just that given the same amount of trials AR is less likely to detect subtle effects than ER?
Oh, one more follow up question. In the paper you are looking at situations where the size of the drift is similar to the difference in the response probabilities of the two arms. Did you look at situations where the size of the drift was 4x or 8x larger than the difference? So one arm’s response rate is 0.32 vs 0.30 but they drift to 0.22 and 0.20.
Dave: Yes, we’re trying to do two things at once, and they are in tension. We’re trying to treat patients in the trial more effectively, and determine an accurate result, which means treating future patients outside the trial more effectively. You can combine these into a single optimization problem by projecting how many future patients will be involved. This depends highly on context. For a very rare disease, maybe there are more patients in the trial than future patients.
Steven: Population drift is a real problem for estimation. It’s not even clear what the correct answer should be if the thing you’re measuring is changing over time.