The security of RSA encryption depends on the fact that the product of two large primes is difficult to factor. So if p and q are large primes, say 2048 bits each, then you can publish n = pq with little fear that someone can factor n to recover p and q.
But if you can change n by a tiny amount, you may make it much easier to factor. The Rowhammer attack does this by causing DRAM memory to flip bits. Note that we’re not talking about breaking someone’s encryption in the usual sense. We’re talking about secretly changing their encryption to a system we can break.
To illustrate on a small scale what a difference changing one bit can make, let p = 251 and q = 643. Then n = pq = 161393. If we flip the last bit of n we get m = 161392. Although n is hard to factor by hand because it has no small factors, m is easy to factor, and in fact
161392 = 24 × 7 × 11 × 131.
For a larger example, I generated two 100-bit random primes in Mathematica
p = 1078376712338123201911958185123
q = 1126171711601272883728179081277
and was able to have it factor n = pq in about 100 seconds. But Mathematica was able to factor n − 1 in a third of a second.
So far we have looked at flipping the least significant bit. But Rowhammer isn’t that precise. It might flip some other bit.
If you flip any bit of a product of two large primes, you’re likely to get an easier factoring problem, though the difficulty depends on the number you start with and which bit you flip. To illustrate this, I flipped each of the bits one at a time and measured how long it took to factor the result.
The median time to factor n with one bit flipped was 0.4 seconds. Here’s a plot of the factoring times as a function of which bit was flipped.
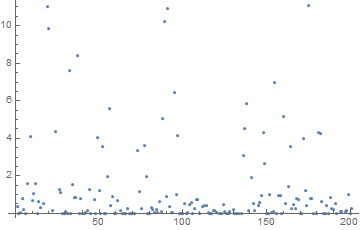
The plot shows about 80% of the data. Twenty percent of the time the value was above 11 seconds, and the maximum value was 74 seconds. So in every case flipping one bit made the factorization easier, usually quite a lot easier, but only a little easier in the worst case.
To verify that the results above were typical, I did a second experiment. This time I generated a sequence of pairs of random 100-bit primes. I factored their product, then factored the product with a randomly chosen bit flipped. Here are the factoring times in seconds.
|----------+---------|
| Original | Flipped |
|----------+---------|
| 117.563 | 3.828 |
| 108.672 | 4.875 |
| 99.641 | 0.422 |
| 103.031 | 0.000 |
| 99.188 | 0.000 |
| 102.453 | 0.234 |
| 79.594 | 0.094 |
| 91.031 | 0.875 |
| 64.313 | 0.000 |
| 95.719 | 6.500 |
| 131.125 | 0.375 |
| 97.219 | 0.000 |
| 98.828 | 0.203 |
|----------+---------|
By the way, we started this post by talking about maliciously flipping a bit. The same thing can happen without a planned attack if memory is hit by a cosmic ray.

Does this help in any way to factor the original n?
No, factoring n-1 doesn’t help you factor n.
This is an interesting article and the whole row hammer bit flipping concept is also interesting.
However, being able to factor a bit flipped n will not let you deduct the original p or q. Are you suggesting that deciphering close p’s and q’s will be a vector to guess the original n?
No, I’m saying an adversary can REPLACE your previous key with a new one. The original n is gone. In its place is an insecure key.
“No, factoring n-1 doesn’t help you factor n.”
It does if n-1 is odd :)
This is a pretty clever insight to apply to Rowhammer though — that if a large integer N is hard to factor, N+a is much easier to factor for almost any value of a.
Neo: “What are you trying to tell me? That I can factor large integers?”
Morpheus: “No, Neo. I’m trying to tell you that when you’re ready, you won’t have to.”
A protection for this would be attempting to factor the key just before each use, though that would add substantially to the amount of computing time for each transaction.
A much simpler and faster method would be generating a checksum or CRC when the key is generated, and saving it with the key. This is much more easily checked before each use. It’s surely a good idea in general, as it also protects from accidental key corruption.