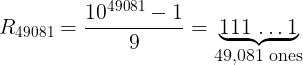The previous post implicitly asserted that J = 8675309 is a prime number. Suppose you wanted proof that this number is prime.
You could get some evidence that J is probably prime by demonstrating that
2J−1 = 1 mod J.
You could do this in Python by running the following [1].
>>> J = 8675309
>>> assert( pow(2, J-1, J) == 1 )
This shows J is a probable prime to base 2.
If you want more evidence, you could also show J is a probable prime to base 3.
>>> assert( pow(3, J-1, J) == 1 )
But no matter how many bases you try, you won’t have proof that J is prime, only evidence. There are pseudoprimes, (rare) composite numbers that satisfy the necessary-but-not-quite-sufficient conditions of Fermat’s primality test.
Primality certificates
A primality certificate is a proof that a number is prime. To be practical, a certificate must be persuasive and efficient to compute.
We could show that J is not divisible by any integer less than √J. That would actually be practical because J is not that large.
>>> for n in range(2, int(J**0.5)+1):
... assert(J % n > 0)
But we’d like to use J to illustrate a method that scales to much larger numbers than J.
Pratt certificates
Pratt primality certificates are based on a theorem by Lucas [2] that says a number n is prime if there exists a number a such that two conditions hold:
an−1 = 1 mod n,
and
a(n−1)/p ≠ 1 mod n
for all primes p that divide n − 1.
How do you find a? See this post.
Example
To find a Pratt certificate for J, we have to factor J − 1. I assert that
J − 1 = 8675308 = 4 × 2168827
and that 2168827 is prime. Here’s verification that Lucas’ theorem holds:
>>> assert( pow(2, (J-1)//2, J) != 1 )
>>> assert( pow(2, (J-1)//2168827, J) != 1 )
What’s that you say? You’re not convinced that 2168827 is prime? Well then, we’ll come up with a Pratt certificate for 2168827.
Pratt certificates are generally recursive. To prove that p is prime, we have to factor p − 1, then prove all the claimed prime factors of p − 1 are prime, etc. The recursion ends when it gets down to some set of accepted primes.
Now I assert that
2168827 − 1 = 2168826 = 2 × 3 × 11 × 17 × 1933
and that all these numbers are prime. I’ll assume you’re OK with that, except you’re skeptical that 1933 is prime.
The following code is proof that 2168827 is prime, assuming 1933 is prime.
>>> m = 2168827
>>> for p in [2, 3, 11, 17, 1933]:
... assert( pow(3, (m-1)//p, m) != 1 )
Finally, we’ll prove that 1933 is prime.
You can verify that
1933 − 1 = 1932 = 2² × 3 × 7 × 23
and I assume you’re convinced that each of these factors is prime.
>>> m = 1933
>>> for p in [2, 3, 7, 23]:
... assert( pow(5, (m-1)//p, m) != 1 )
Pratt certificates can be written in a compact form that verification software can read. Here I’ve made the process more chatty just to illustrate the parts.
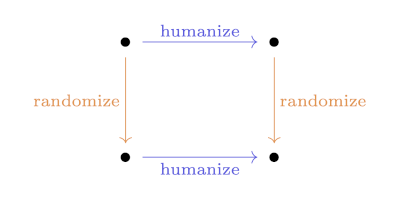
Update: Here’s a visualization of the process above, drawing arrows from each prime p to the prime factors of p − 1.
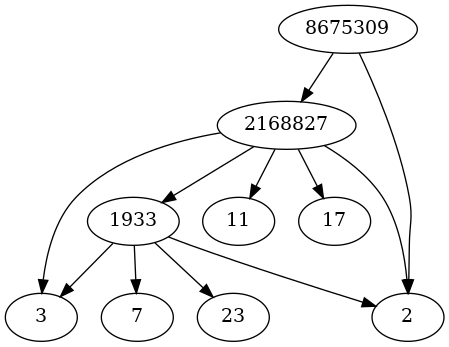
In this post we’ve agree to recognize 2, 3, 7, 11, 17, and 23 as primes. But you only have to assume 2 is prime. This would make the software implementation more elegant but would make the example tedious for a human consumption.
Efficiency
A primality certificate does not have to be efficient to produce, though of course that would be nice. It has to be efficient to verify. You could imagine that the prime number salesman has more compute power available than the prime number customer. In the example above, I used a computer to generate the Pratt certificate, but it wouldn’t be unreasonable to verify the certificate by hand.
The brute force certificate above, trying all divisors up to √p, obviously takes √p calculations to verify. A Pratt certificate, however, takes about
4 log2 p
calculations. So verifying a 10-digit prime requires on the order of 100 calculations rather than on the order of 100,000 calculations.
Atkin-Goldwasser-Kilian-Morain certificates
Producing Pratt certificates for very large numbers is difficult. Other certificate methods, like Atkin-Goldwasser-Kilian-Morain certificates, scale up better. Atkin-Goldwasser-Kilian-Morain certificates are more complicated to describe because they involve elliptic curves.
Just as Pratt took a characterization of primes by Lucas and turned it into a practical certification method, Atkin and Morain turned a characterization of primes by Goldwasser and Kilian, one involving elliptic curves, and turned it into an efficient certification method.
These certificates have the same recursive nature as Pratt certificates: proving that a number is prime requires proving that another (smaller) number is prime.
Update: More on elliptic curve primality proofs.
***
[1] This is a more efficient calculation than it seems. It can be done quickly using fast exponentiation. Note that it is not necessary to compute 2J−1 per se; we can carry out every intermediate calculation mod J.
[2] Lucas was French, and so the final s in his name is silent.