If we have two unrelated sequences of DNA, how long would we expect the longest common substring of the two sequences to be? Since DNA sequences come from a very small alphabet, just four letters, any two sequences of moderate length will have some common substring, but how long should we expect it to be?
Motivating problem
There is an ongoing controversy over whether the SARS-CoV-2 virus contains segments of the HIV virus. The virologist who won the Nobel Prize for discovering the HIV virus, Luc Montagnier, claims it does, and other experts claim it does not.
I’m not qualified to have an opinion on this dispute, and do not wish to discuss the dispute per se. But it brought to mind a problem I’d like to say something about.
This post will look at a simplified version of the problem posed by the controversy over the viruses that cause COVID-19 and AIDS. Namely, given two random DNA sequences, how long would you expect their longest common substring to be?
I’m not taking any biology into account here other than using an alphabet of four letters. And I’m only looking at exact substring matches, not allowing for any insertions or deletions.
Substrings and subsequences
There are two similar problems in computer science that could be confused: the longest common substring problem and the longest common subsequence problem. The former looks for uninterrupted matches and the latter allows for interruptions in matches in either input.
For example, “banana” is a subsequence of “bandana” but not a substring. The longest common substring of “banana” and “anastasia” is “ana” but the longest common subsequence is “anaa.” Note that the latter is not a substring of either word, but a subsequence of both.
Here we are concerned with substrings, not subsequences. Regarding the biological problem of comparing DNA sequences, it would seem that a substring is a strong form of similarity, but maybe too demanding since it allows no insertions. Also, the computer science idea of a subsequence might be too general for biology since it allows arbitrary insertions. A biologically meaningful comparison would be somewhere in between.
Simulation results
I will state theoretical results in the next section, but I’d like to begin with a simulation.
First, some code to generate a DNA sequence of length N.
from numpy.random import choice
def dna_sequence(N):
return "".join(choice(list("ACGT"), N))
Next, we need a way to find the longest common substring. We’ll illustrate how SequenceMatcher works before using it in a simulation.
from difflib import SequenceMatcher
N = 12
seq1 = dna_sequence(N)
seq2 = dna_sequence(N)
# "None" tells it to not consider any characters junk
s = SequenceMatcher(None, seq1, seq2)
print(seq1)
print(seq2)
print(s.find_longest_match(0, N, 0, N))
This produced
TTGGTATCACGG
GATCACAACTAC
Match(a=5, b=1, size=5)
meaning that the first match of maximum length, ATCAC in this case, starts in position 5 of the first string and position 1 of the second string (indexing from 0).
Now let’s run a simulation to estimate the expected length of the longest common substring in two sequences of DNA of length 300. We’ll do 1000 replications of the simulation to compute our average.
def max_common_substr_len(a, b):
# The None's turn off junk detection heuristic
s = SequenceMatcher(None, a, b, None)
m = s.find_longest_match(0, len(a), 0, len(b))
return m.size
seqlen = 300
numreps = 1000
avg = 0
for _ in range(numreps):
a = dna_sequence(seqlen)
b = dna_sequence(seqlen)
avg += max_common_substr_len(a, b)
avg /= numreps
print(avg)
When I ran this code I got 7.951 as the average. Here’s a histogram of the results.
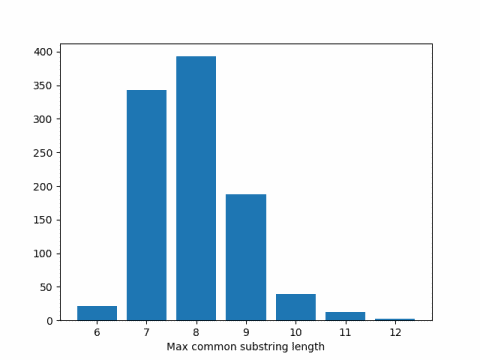
Expected substring length
Arratia and Waterman [1] published a paper in 1985 looking at the longest common substring problem for DNA sequences, assuming each of the four letters in the DNA alphabet are uniformly and independently distributed.
They show that for strings of length N coming from an alphabet of size b, the expected length of the longest match is asymptotically
2 logb(N).
This says in our simulation above, we should expect results around 2 log4(300) = 8.229.
There could be a couple reasons our simulation results were smaller than the theoretical results. First, it could be a simulation artifact, but that’s unlikely. I repeated the simulation several times and consistently got results below the theoretical expected value. I expect Arratia and Waterman’s result, although exact in the limit, is biased upward for finite n.
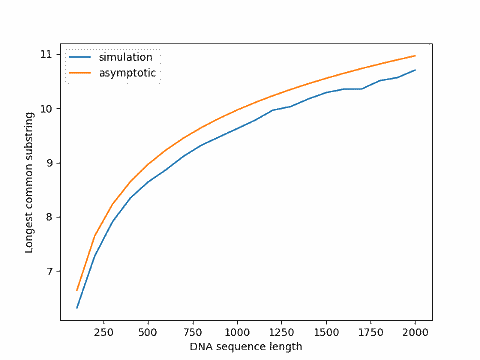
Update: The graph below plots simulation results for varying sequence sizes compared to the asymptotic value, the former always below the latter.
Arratia and Waterman first assume i.i.d. probabilities to derive the result above, then prove a similar theorem under the more general assumption that the sequences are Markov chains with possibly unequal transition probabilities. The fact that actual DNA sequences are not exactly uniformly distributed and not exactly independent doesn’t make much difference to their result.
Arratia and Waterman also show that allowing for a finite number of deletions, or a number of deletions that grows sufficiently slowly as a function of n, does not change their asymptotic result. Clearly allowing deletions makes a difference for finite n, but the difference goes away in the limit.
Related posts
[1] Richard Arratia and Michael S. Waterman. An Erdős-Rényi Law with Shifts. Advances in Mathematics 55, 13-23 (1985).

Réndi -> Rényi