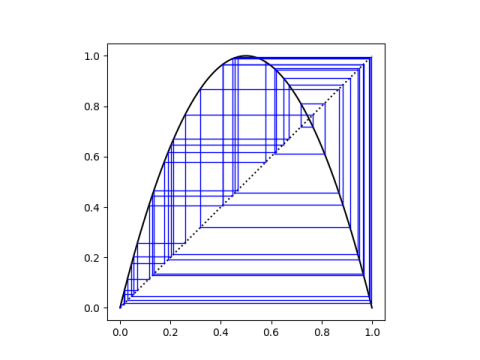
Is 0 a stable fixed point of f(x) = 4x (1-x)?
If you set x = 0 and compute f(x) you will get exactly 0. Apply f a thousand times and you’ll never get anything but zero.
But this does not mean 0 is a stable attractor, and in fact it is not stable.
It’s easy to get mathematical stability and numerical stability confused, because the latter often illustrates the former. In this post I point out that the points on a particular unstable orbit cannot be represented exactly in floating point numbers, so iterations that start at the floating point representations of these points will drift away.
In the example here, 0 can be represented exactly, and so we do have a computationally stable fixed point. But 0 is not a stable fixed point in the mathematical sense. Any starting point close to 0 but not exactly 0 will eventually go all over the place.
If we start at some very small ε > 0, then f(ε) ≈ 4ε. Every iteration multiplies the result by approximately 4, and eventually the result is large enough that the approximation no longer holds.
For example, suppose we start with x = 10-100. After 100 iterations we have
x = 4100 10-100 = 1.6 × 10-40.
If we were to plot this, we wouldn’t see any movement. But by the time we iterate our function 200 times, the result is chaotic. I get the following: