The exponential sum page on this site draws lines between the consecutive partial sums of
where m is the month, d is the day, and y is the last two digits of the year.
I get mixed feedback on my exponential sum page. Some people find it even more interesting than I do and have asked permission to use the images [1]. Others tell me they don’t understand what the big deal is. I find the images interesting, and I’d like to give some explanation why.
What I like about these images is that they’re somewhere between predictable and mysterious. The particular sum above has a few properties that aren’t hard to derive, but it’s also full of surprises. This is true of exponential sums more generally.
Exponential sums can be deep and subtle. See, for example, the course description and lecture notes here. If you eliminate the linear and cubic components in the sum above, conceptually setting m and y to infinity, and d is a prime number, then you get the Gauss sums, a topic of particular interest in the lecture notes.
The contrast between images for consecutive days illustrates the fact that number theory has its own way of measuring differences (e.g. p-adic numbers). So, for example, while today’s date [2], 5/26/2021, is close to yesterday’s date, 5/25/2021, the corresponding images

and
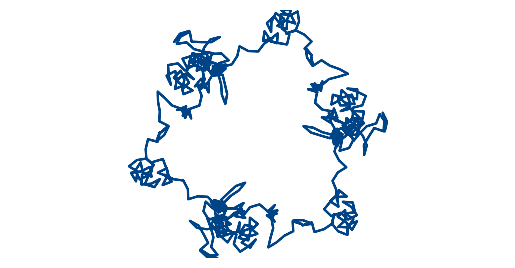
are very different because from a number theoretic perspective the triples (5, 26, 21) and (5, 25, 21) are not close together. The individual terms in the sums are close together, because 1/25 is close to 1/26, but the sums have quite different behavior.
Estimating exponential sums and proving things about them requires its own set of techniques. If you just apply the usual techniques you’d use on general sums, your estimates will be so far from optimal as to be useless.
I’m not an expert in exponential sums. When I look at the images my site produces I know that something is going on deeper than I understand, even though I can’t say what it is. That’s how most of the world is—there’s more to my car, or my dog, or even my fingernail than I’ll ever understand—but it’s even true of much simpler things, like exponential sums.
Related posts
[1] If you’d like to use one of the images, go ahead. But rather than taking a screen shot, send me an email and I can give you a higher resolution image or an SVG file.
[2] I understand the objections to the American way of writing dates, but I thought the exponential sum page worked out to be more interesting basing it on this format. I prefer the ISO date format to both American and European conventions.
