It’s not obvious when a nonlinear differential equation will have a periodic solution, or asymptotically approach a periodic solution. But there are theorems that give sufficient conditions. This post is about one such theorem.
Consider the equation
x” + f(x) x‘ + g(x) = 0
where f and g are analytic and define F(x) to be the integral of f(t) from 0 to x. The following six hypotheses are sufficient to guarantee that the equation above has a stable limit cycle [1].
- g is an odd function,
- g is positive for positive x,
- f is an even function,
- f(o) < 0,
- F(x) → ∞ as x → ∞,
- F has a unique positive zero.
These hypotheses are satisfied, for example, by Van der Pol’s equation.
Let’s make up coefficient functions f and g that satisfy the conditions above and look for the limit cycle.
We can let g(x) = x³ and f(x) = x² − 1. And here’s what we get:
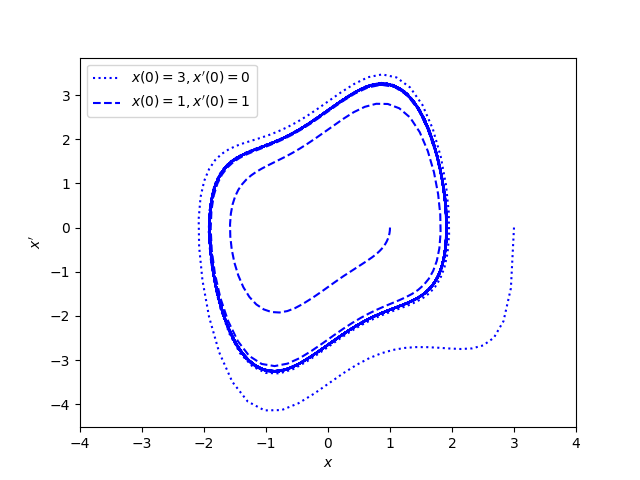
The graph shows phase portraits for two different initial conditions, given in the legend of the plot. Note that limit cycle appears solid blue because the trajectories of both the dashed line and the dotted line run around the periodic attractor.
Related posts
[1] You can find this theorem in Topics in Ordinary Differential Equations by William Lakin and David Sanchez.

I think you meant x” + f(x) x’ + g(x); or if g(x) x, then g(x) should be an even function. Your figure seems to show x” + (x^2 – 1) x’ + x^3.
Nice post!