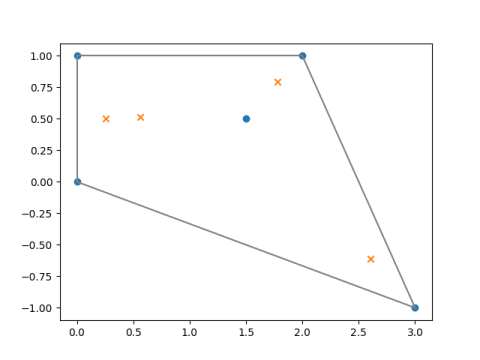
There’s a well-known theorem in complex analysis that says that if p is a polynomial, then the zeros of its derivative p′ lie inside the convex hull of the zeros of p. The convex hull of a set of points is the smallest convex set containing those points.
This post gives a brief illustration of the theorem. I created a polynomial with roots at 0, i, 2 + i, 3-i, and 1.5+0.5i. The convex hull of these points is the quadrilateral with corners at the first four roots; the fifth root is inside the convex hull of the other roots.
The roots are plotted with blue dots. The roots of the derivative are plotted with orange ×’s.
In the special case of cubic polynomials, we can say a lot more about where the roots of the derivative lie. That is the topic of the next post.

Check out this cute proof using electrostatics:
https://johncarlosbaez.wordpress.com/2021/05/24/electrostatics-and-the-gauss-lucas-theorem/