The previous post was a warmup for this post. It gave an example of the theorem that if p is a polynomial, the roots of its derivative p′ lie inside the convex hull of the roots of p. If p is a cubic polynomial, we can say much more.
Suppose p(z) is a polynomial with three distinct roots, not all on a line. Then the roots of p are the vertices of a triangle T in the complex plane. We know that the roots of p′ lie inside T, but Marden’s theorem says where they lie inside T.
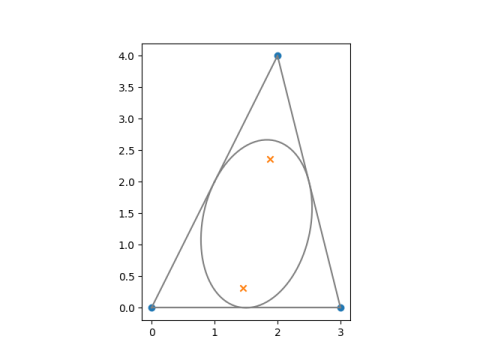
Let E be the unique ellipse inscribed inside T that touches T at the midpoint of each side. Then Marden’s theorem says that the roots of p′ lie on the foci of E.
The ellipse E is sometimes called the Steiner inellipse.
For an example, let
p(z) = z (z – 3) (z – 2 – 4i)
The roots of the derivative of p are 1.4495 + 0.3100i and 1.8838 + 2.3566i.
Here’s a plot of the roots of p (blue dots), the roots of p′ (orange ×), and the Steiner ellipse. I used a parametric equation for the Steiner ellipse from here.

Might want to add that p’ is the derivative of p to this blog too. Had to click the other one to see what it was, thought it might have been some other polynomial.