The previous post included this image of a logarithm spiral passing through the corners of squares in a sequence of golden rectangles.
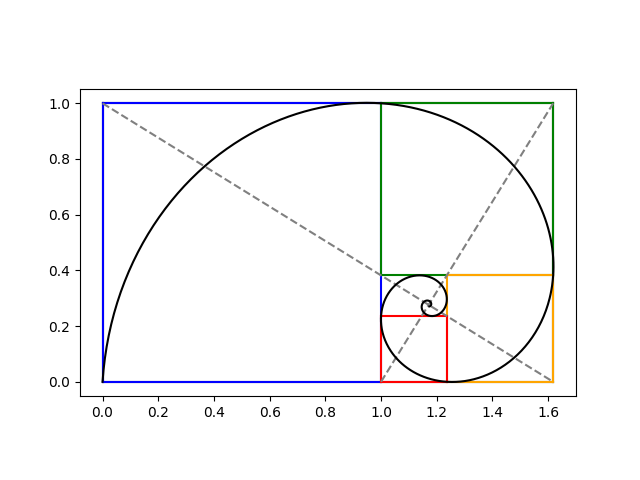
The portion of the spiral in each square looks like a quarter of a circle. How well would circular arcs approximate the spiral?
Very well. Here’s a plot.
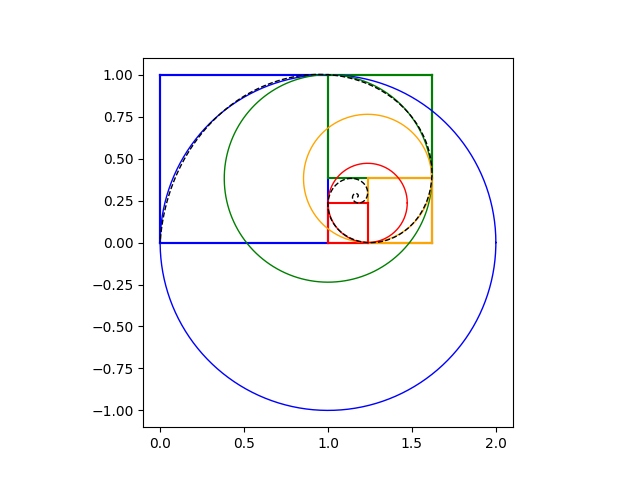
The circular arc inside the blue square is plotted in blue, the arc inside the green box in green, etc. The logarithmic spiral is plotted on top with a dashed black line. You have to zoom in closely to see any difference between the logarithmic spiral and its circular approximations.
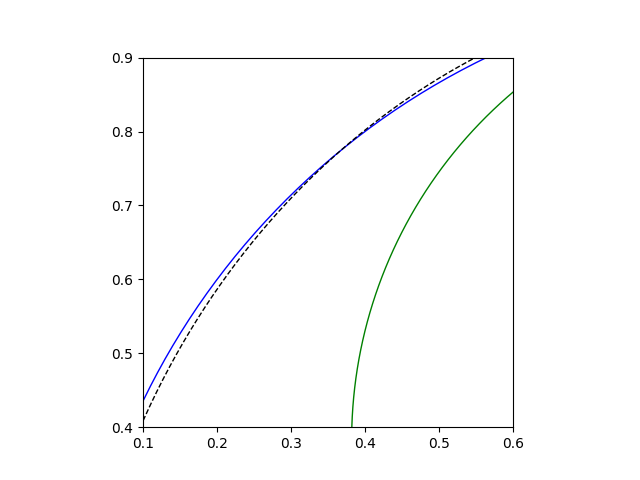
For aesthetic applications, circular arcs are good enough and probably easier to work with. For a sort of three-dimensional analog of this approximation, see this post on the geometry of the Sydney Opera House.
Sometimes discontinuities in first or second derivatives are visually noticeable, but here they’re not. The approximation of the logarithmic spiral by a sequence of quarter circles has a jumps in curvature, which is roughly a second derivative. I suppose it’s more noticeable when curvature jumps from positive to zero or from positive to negative. Here it’s jumping from one positive value (the reciprocal of the circle radius) to another positive value (the reciprocal of a smaller radius).

@”The approximation of the logarithmic spiral by a sequence of quarter circles has a jumps in curvature”
That means, you can’t drive along this approximation by car.
Driving along it by train will result in unpleasant sudden changes in lateral acceleration. See:
https://en.wikipedia.org/wiki/Track_transition_curve
https://en.wikipedia.org/wiki/Euler_spiral
(+ tiny typo: superfluous a before jumps)