Conformal map between square and disk

Conformal maps transform one region into another while preserving angles. You might solve a PDE, for example, by mapping it to a standard region, solving it there, then mapping the solution back to the original region.

Some tasks are easier to do in a square and others in a disk, so it’s clearly useful to be able to conformally map between squares and disks. The Riemann mapping theorem tells us this can be done, but it doesn’t tell us how. Two gentlemen figured out how to map between squares (and more general polygons) and disks in the 1860s: Hermann Schwarz and Elwin Christoffel. Schwarz is known for many different results in analysis, including the topic of the previous post, the conformal map from an ellipse to the unit disk. Christoffel is best known for Christoffel symbols, building blocks of tensors.

Here’s a plot showing how the Schwarz-Christoffel transformation from the square [−1, 1] × [−1, 1] to the unit disk transforms Cartesian grid lines.

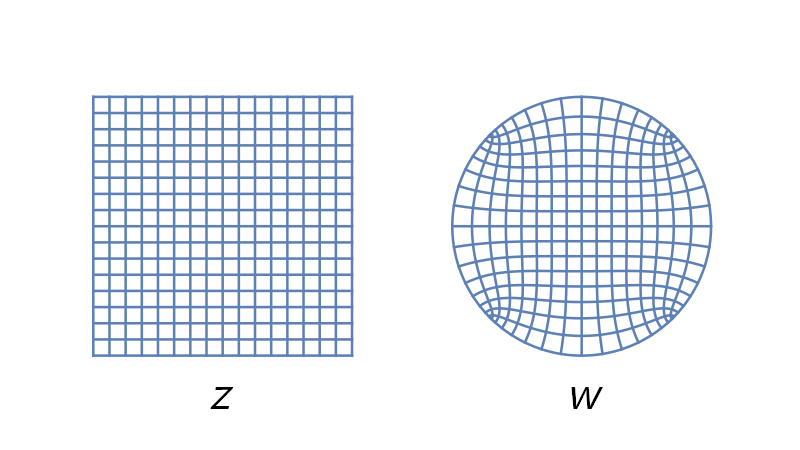
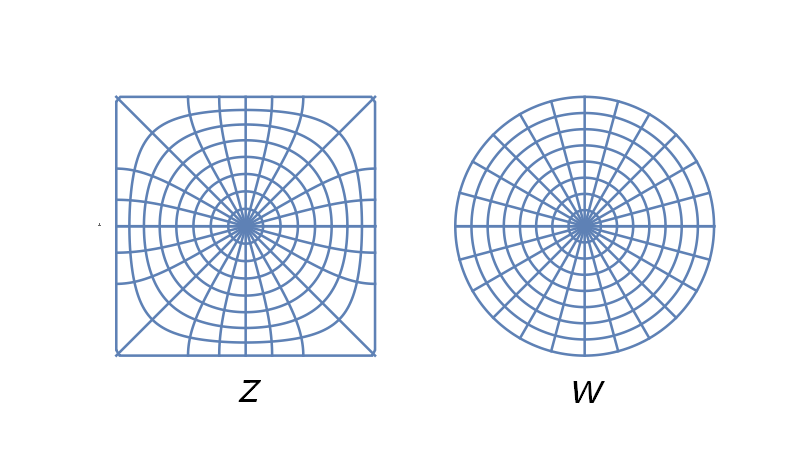
Here’s another plot, this one showing how the grid lines for polar coordinates on the disk pull back to curves on the square.

Equations

The equation for the function from the square to the disk is

where sd is a Jacobi elliptic function with parameter 1/2 [1]. The constant K is the complete elliptic function of the first kind, evaluated at 1/2. In symbols, K = K(1/2).

The inverse function has equation

Here F is the incomplete elliptic function of the first kind. For more background, see this post on kinds of elliptic integrals.

Fast approximation

An exact map from the square to the disk requires elliptic functions. However, there is a simple polynomial approximation to the map above [2].

Peirce’s projection

Charles Sanders Peirce used the conformal map of the disk to the square to create the “Peirce quincuncial projection” map. This is a conformal (i.e. angle-preserving) map that represents the globe on a square. The diamond shape in the middle is the image of the equator. The mapping is singular at the south pole.

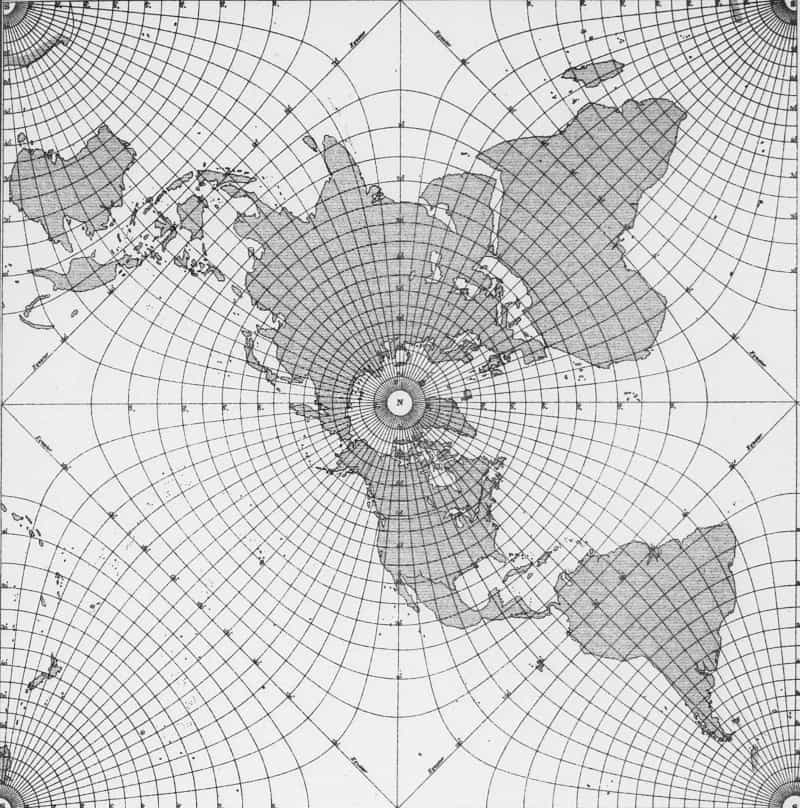
Peirce named the map after the quincunx pattern of the poles. This obscure word refers to the pattern of dots on the five face of a standard six-sided die.

Related posts

• Conformal map from ellipse to disk
• Conformal mapping and Laplace’s equation
• Applied complex analysis

[1] “Parameter” is being used in a technical sense here. There are two conventions for describing the parameterization of elliptic functions and elliptic functions and elliptic integrals, and here we are using the parameter called The Parameter, commonly denoted m. There’s another convention that uses the elliptic modulus k, and the connection between them is that m = k².

[2] Prem K. Kythe. Handbook of Conformal Mappings and Applications. CRC Press. Page 286.