{div, grad, curl} of a {div, grad, curl}

The various combinations of divergence, gradient, and curl are confusing to someone seeing them for the first time, and even for someone having seen them many times. Is the divergence of a curl zero or is it the divergence of a gradient that’s zero? And there’s another one, Is it curl of curl or or curl of grad that’s zero?

It’s a mess that’s hard to sort out without pulling out differential forms. This post will show how a calculus student could make some sense out of all this, and how differential forms clarify the situation further.

Vector calculus perspective

We’ll start out looking at things from the perspective of a calculus student. We can make a table of all nine possible combinations of {grad, curl, div} applied to a {grad, curl, div} and start by asking which combinations make sense.

Gradient is something that takes a scalar function and returns a vector field. Curl takes a vector field and returns another vector field. Divergence takes a vector field and returns a scalar function. This means that only five of our nine combinations are even defined.

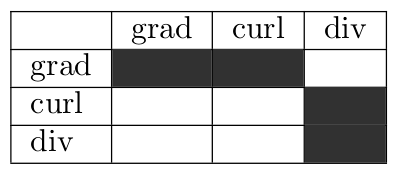
It turns out that the divergence of a curl is zero, and the curl of a gradient is zero (the zero vector). The other three possibilities are defined, but they are not zero in general.

So we can extend our chart to include the zeros.

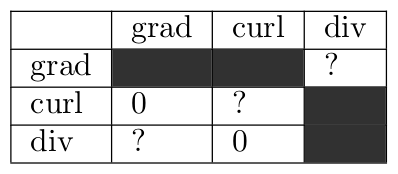
Plain text version of chart image included at the bottom of the post.

Differential form perspective

From the perspective of differential forms, a scalar function f is a 0-form.

The differential of a 0-form is a 1-form and corresponds to the gradient.

The differential of a 1-form is a 2-form and corresponds to curl.

The differential of a 2-form is a 3-form and corresponds to divergence.

The differential of a differential is 0: d² = 0. This holds for k forms in general, for any non-negative integer k. So the curl of a gradient is 0 and the divergence of a curl is 0.

Gradients are 1-forms and curls are 2-forms. They’re different kinds of things. Vector calculus hides this distinction, which initially makes things simpler but ultimately makes things harder.

Now what about the three possibilities marked with question marks in the table above: the divergence of a gradient, the curl of a curl, and the gradient of a divergence?

From the perspective of differential forms, these are illegal operations. You cannot take the divergence of a gradient, because divergence operates on 2-forms, and a gradient is a 1-form. Similarly, you cannot take the curl of a curl or the gradient of a divergence. You could think of differential forms as adding type-checking to vector calculus.

But operations like taking the divergence of a gradient are legal in vector calculus. What gives?

Hodge star

The Hodge star operator is a duality between k-forms and (n–k)-forms. In vector calculus n = 3, and so the Hodge star takes 0-forms to 3-forms and 3-forms to 0-forms.

f ︎↔︎ f dx dy dz

It also takes 1-forms to 2-forms and 2-forms to 1-forms.

f dx + g dy + h dz ︎↔︎ f dy dz + g dz dx + h dx dy.

You can’t take the divergence of a gradient of a function f, but you can translate the 1-form df represents into the 2-form *df via the Hodge operator, then take the divergence of that. This gives you a 3-form d*df, which you can translate to a 0-form by applying * once more to get *d*df. So the Laplacian, defined to be the divergence of the gradient in vector calculus, is *d*d in the language of differential forms.

Curl takes 1-forms to 2-forms, so you can’t take the curl of a curl. But you can turn a curl into a 1-form via the Hodge operator and then take the curl of that. And while you can’t take the divergence of a gradient, you can take the divergence of the Hodge operator applied to a gradient.

In vector calculus the Hodge operator is invisible. Making it visible explains why some combinations of operators always result in zeros and some do not: some identities follow from the general identity d² = 0, but operations requiring a Hodge operator are not zero in general.

The Hodge star operator is not so simple in general as it is in Euclidean space. On a Riemann manifold the Hodge operator is defined in terms of the metric. Defining the Laplace operator as *d*df extends to Riemann manifolds, but defining it as the sum of second partial derivatives will not.

Related posts

• Exact sequences
• Elliptic coordinates
• Four meanings of ^

Plain text chart:

|------+------+------+-----|
|      | grad | curl | div |
|------+------+------+-----|
| grad | NA   | NA   | ?   |
| curl | 0    | ?    | NA  |
| div  | ?    | 0    | NA  |
|------+------+------+-----|