
In 1881, astronomer Simon Newcomb noticed something curious. The first pages in books of logarithms were dirty on the edge, while the pages became progressively cleaner in later pages. He inferred from this that people more often looked up the logarithms of numbers with small leading digits than with large leading digits.
Why might this be? One might reasonably expect the numbers that came up in work to be uniformly distributed. But as often the case, it helps to ask “Uniform on what scale?”
Newcomb might have imagined his counterpart on another planet. This alien astronomer might have 12 fingers [1] and count in base 12. Base 10 is not inevitable, even for creatures with 10 fingers: the ancient Sumerians used a base-60 number system.
If Newcomb’s twelve-fingered counterpart had developed logarithms but not digital computers, he might have tables of duodecimal logarithms bound into books, and he too might noticed that pages with small leading (duo)digits are more frequently referenced. Both astronomers would naturally look up the logarithms of physical constants, physical distances, and so fort, numbers that vary over a practically unlimited range. The unlimited range is important.
On what scale could both astronomers see the leading digits uniformly distributed?
If Newcomb needed to look up the logarithms of numbers over a limited range, say from 1 to 106, each with equal probability, then the leading digits would be uniformly distributed. But our alien astronomer would have no special interest in the number 106. He might want to look at numbers between 1 and 126. The leading digits of numbers over this range would be uniformly distributed when represented in base 12, but not when represented in base 10. The choice of upper limit introduces a bias in one base or another.
Now suppose the numbers that both astronomers used in their work were uniformly distributed on a logarithmic scale. Newcomb conjectured that the numbers that came up in practice were uniformly distributed in their logarithms base 10. Our alien astronomer might conjecture the same thing for logarithms base 12. And both could be right. So would a third astronomer working in base 42. All logarithms are proportional, and so numbers uniformly distributed on a log scale using one base are uniformly distributed on a log scale using any other base.
Benford’s law says that the leading digits of numbers that come up in practice are uniformly distributed on a log scale. This applies to base 10, but also any other base, such as base 100. If you looked at the first two digits and thought of them as single base-100 digits, Benford’s law still applies.
But who is Benford? True to Stigler’s law of eponymy, Newcomb’s observation is named after physicist Frank Benford who independently made the same observation in 1938 and who tested it more extensively.
Let’s look at a set of physical constants and see how well Benford’s law applies. I took at list of physical constants from NIST and made a histogram of the leading digits to compare with what one would expect from Benford’s law.
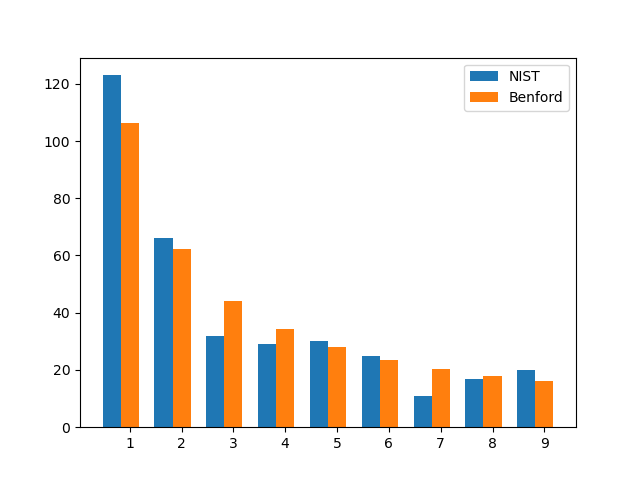
If one were to write the NIST constants in base 12 and repeat the exercise, the result would look similar.
Related posts
[1] The image at the top of the post was created by DALL-E. There is a slight hint of an extra finger. DALL-E usually has a hard problem with hands, adding or removing fingers. But my attempts to force it to draw a hand with an extra finger were not successful.

Comments are closed.