Eccentricity of bivariate normal level sets

Posted on by John

Suppose you have a bivariate normal distribution with correlation ρ where

f(x,y) = \frac{1}{2\pi \sqrt{1-\rho^2}} \exp\left(-\frac{x^2 - 2\rho xy + y^2}{2(1-\rho^2)} \right)

Then the level sets of the density function are ellipses, and the eccentricity e of the ellipses is related to the correlation ρ by

\begin{align*} \rho &= \pm \frac{e^2}{2 - e^2} \\ e &= \sqrt{\frac{2|\rho|}{1 + |\rho|} } \end{align*

Plots

For example, suppose ρ = 0.8.

Here’s a plot of the density function f(x, y).

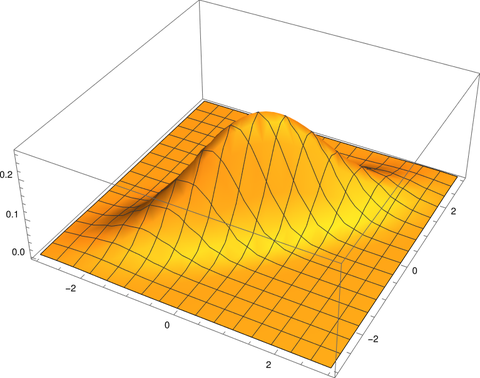
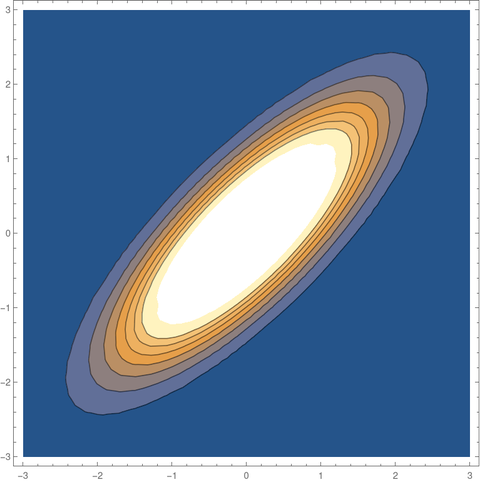
And here is a plot of the contours, the level sets obtained by slicing the plot of the density horizontally.

Eccentricity and aspect ratio

The equation above says that since ρ = 0.8 the eccentricity e should be √(1.6/1.8) = 0.9428.

As I’ve written about several times, eccentricity is a little hard to interpret. It’s a number between 0 and 1, with 0 being a circle and 1 being a degenerate ellipse collapsed to a line segment. Since 0.9428 is closer to 1 than to 0, you might think that an ellipse with such a large value of e is very far from circular. But this is not the case.

Eccentric literally means off-center. Eccentricity measures how far off-center the foci of an ellipse are. This is related to how round or thin an ellipse is, but only indirectly. It is true that such a large value of e means that the foci are close to the ends of the ellipse. In fact, the foci are located at 94.28% of the distance from the center to the end of the semimajor axes. But the aspect ratio is more moderate.

It’s easier to imagine the shape of an ellipse from the aspect ratio than from the eccentricity. Aspect ratio r is related to eccentricity e by

r = \sqrt{1-e^2}

Using the expression above for eccentricity e as a function of correlation ρ we have

r = \sqrt{\frac{1 - |\rho|}{1 + |\rho|}}

This says our aspect ratio should be 1/3. So although our ellipse is highly eccentric—the foci are near the ends—it isn’t extraordinarily thin. It’s three times longer than it is wide, which matches the contour plot above.

Related posts

One thought on “Eccentricity of bivariate normal level sets”

  1. > “our aspect ratio should be 1/3. … It’s three times longer than it is wide”

    Just to clarify, the “aspect ratio” does not refer to the ratio of the Euclidean ranges for X and Y. Rather, this result is independent of the orientation of the ellipse and refers to the ratio of the axes of the ellipse. If L_maj is the length of the semimajor axis and L_min is the length of the semiminor axis, then L_min = L_maj*sqrt(1 – e^2). You can rewrite this as
    L_min/L_maj = sqrt(1 – e^2) = r

    Readers familiar with principal components might remember that the lengths of the axis of the probability ellipse are 1/sqrt(lambda_1) and 1/sqrt(lambda_2), where lambda_1 and lambda_2 are the eigenvalue of the covariance matrix, which is [1 0.8; 0.8 1] for this example. The eigenvalues of this matrix are 9/5 and 1/5. So, as claimed, the ratio of the square roots is sqrt(1/5)/sqrt(9/5) = 1/3.

Comments are closed.