Ramanujan’s nested radical

Posted on 13 September 2013 by John

Ramanujan posed the following puzzle to Journal of Indian Mathematical Society. What is the value of the following?

$\sqrt{1+2\sqrt{1+3 \sqrt{1+4\sqrt{1 + \cdots}}}}$

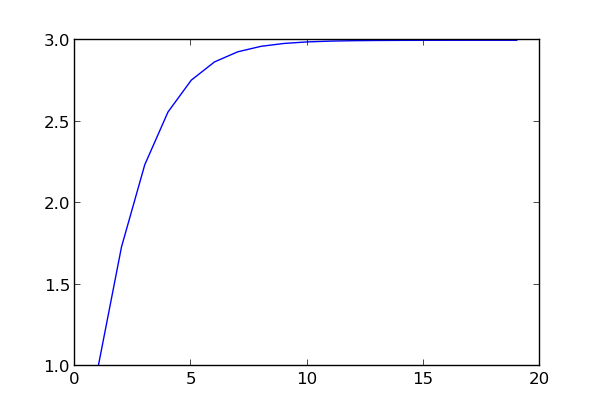
He waited over six months, and when nobody replied he gave his solution. The result is simply 3.

Now suppose you didn’t know an algebraic proof and wanted to evaluate the expression numerically. The code below will evaluate Ramanujan’s expression down to n levels.

def f(n):
    t = 1.0
    for k in range(n, 1, -1):
        t = sqrt(k*t + 1)
    return t

(The range function above produces the sequence n, n-1, … 2.)

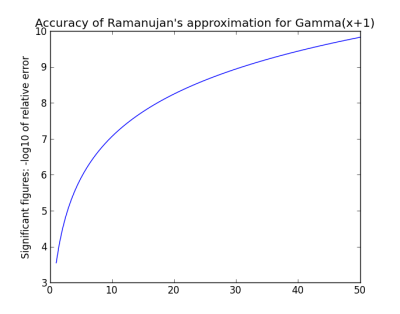
The sequence of f(n) values converges rapidly to 3 as the plot below shows.

The code above evaluates the expression from the inside out, and so you need to know where you’re going to stop before you start. I don’t see how to write a different algorithm that would let you compute f(n+1) taking advantage of having computed f(n). Do you? Can you think of a way to evaluate f(1), f(2), f(3), … f(N) in less than O(N²) time? Will your algorithm if some or all of the numbers in Ramanujan’s expression change?

Ramanujan approximation for circumference of an ellipse

Posted on 5 May 2013 by John

Ramanujan

There’s no elementary formula for the circumference of an ellipse, but there is an elementary approximation that is extremely accurate.

An ellipse has equation (x/a)² + (y/b)² = 1. If a = b, the ellipse reduces to a circle and the circumference is simply 2πa. But the general formula for circumference requires the hypergeometric function ₂F₁:

$\setlength\arraycolsep{1pt} \pi (a + b) \, {}_2 F_1\left(\begin{matrix}-1/2& &-1/2 \\&1& \end{matrix}\middle;\lambda^2\right)$

where λ = (a − b)/(a + b).

However, if the ellipse is anywhere near circular, the following approximation due to Ramanujan is extremely good:

$\pi (a + b) \left(1 + \frac{3\lambda^2}{10 + \sqrt{4 - 3\lambda^2}}\right)$

To quantify what we mean by extremely good, the error is O(λ¹⁰). When an ellipse is roughly circular, λ is fairly small, and the error is on the order of λ to the 10th power.

To illustrate the accuracy of the approximation, I tried the formula out on some planets. The error increases with ellipticity, so I took the most elliptical orbit of a planet or object formerly known as a planet. That distinction belongs to Pluto, in which case λ = 0.016. If Pluto’s orbit were exactly elliptical, you could use Ramanujan’s approximation to find the circumference of its orbit with an error less than one micrometer.

Next I tried it on something with a much more elliptical orbit: Halley’s comet. Its orbit is nearly four times longer than it is wide. For Halley’s comet, λ = 0.59 and Ramanujan’s approximation agrees with the exact result to seven significant figures. The exact result is 11,464,319,022 km and the approximation is 11,464,316,437 km.

Here’s a video showing how elliptical the comet’s orbit is.

If you’d like to experiment with the approximation, here’s some Python code:

    from scipy import pi, sqrt
    from scipy.special import hyp2f1

    def exact(a, b):
        t = ((a-b)/(a+b))**2
        return pi*(a+b)*hyp2f1(-0.5, -0.5, 1, t)

    def approx(a, b):
        t = ((a-b)/(a+b))**2
        return pi*(a+b)*(1 + 3*t/(10 + sqrt(4 - 3*t)))

    # Semimajor and semiminor axes for Halley's comet orbit
    a = 2.667950e9 # km
    b = 6.782819e8 # km

    print exact(a, b)
    print approx(a, b)

Ramanujan’s most beautiful identity

Posted on 27 October 2012 by John

G. H. Hardy called the following equation Ramanujan’s “most beautiful identity.”

For |q| < 1,

$\sum_{n=0}^\infty p(5n+4) q^n = 5 \prod_{n=1}^\infty \frac{(1 - q^{5n})^5}{(1 - q^n)^6}$

If I understood it, I might say it’s beautiful, but for now I can only say it’s mysterious. Still, I explain what I can.

The function p on the left side is the partition function. For a positive integer argument n, p(n) is the number of ways one can write n as the sum of a non-decreasing sequence of positive integers.

The right side of the equation is an example of a q-series. Strictly speaking it’s a product, not a series, but it’s the kind of thing that goes under the general heading of q-series.

I hardly know anything about q-series, and they don’t seem very motivated. However, I keep running into them in unexpected places. They seem to be a common thread running through several things I’m vaguely familiar with and would like to understand better.

As mysterious as Ramanujan’s identity is, it’s not entirely unprecedented. In the eighteenth century, Euler proved that the generating function for partition numbers is a q-product:

$\sum_{n=0}^\infty p(n) q^n = \prod_{n=1}^\infty \frac{1}{(1 - q^n)}$

So in discovering his most beautiful identity (and others) Ramanujan followed in Euler’s footsteps.

Reference: An Invitation to q-series

Ramanujan pi approximation

Posted on 8 October 2012 by John

Here’s a mysterious approximation to π from Ramanujan:

$pi approx frac{12}{sqrt{190}} logleft( (2sqrt{2} + sqrt{10})(3 + sqrt{10})right)$

The approximation is correct to 18 decimal places. I have no idea what inspired it.

Open question turned into exercise

Posted on 2 October 2012 by John

G. H. Hardy tells the following story about visiting his colleague Ramanujan.

I remember once going to see him when he was ill at Putney. I had ridden in taxi cab number 1729 and remarked that the number seemed to me rather a dull one, and that I hoped it was not an unfavorable omen. “No,” he replied, “it is a very interesting number; it is the smallest number expressible as the sum of two cubes in two different ways.”

This story has become famous, but the rest of the conversation isn’t as well known. Hardy followed up by asking Ramanujan what the corresponding number would be for 4th powers. Ramanujan replied that he did not know, but that such a number must be very large.

Hardy tells this story in his 1937 paper “The Indian Mathematician Ramanujan.” He gives a footnote saying that Euler discovered 635318657 = 158^4 + 59^4 = 134^4 + 133^4 and that this was the smallest number known to be the sum of two fourth powers in two ways. It seems odd now to think of such questions being unresolved. Today we’d ask Hardy “What do you mean 635318657 is the smallest known example? Why didn’t you write a little program to find out whether it really is the smallest?”

Surely someone has since written such a program and settled the question. But as an exercise, imagine the question is still open. Write a program to either come up with a smaller number that answer’s Hardy’s question, or prove that Euler’s number is the smallest one. To make the task more interesting, you might see whether you could do a little pencil-and-paper math up front to reduce the amount searching needed. Also, you might try writing the program in different styles: imperative, functional, etc.

Ramanujan’s factorial approximation

Posted on 25 September 2012 by John

Ramanujan came up with an approximation for factorial that resembles Stirling’s famous approximation but is much more accurate.

$n! \sim \sqrt{\pi} \left(\frac{n}{e}\right)^n \sqrt[6]{8n^3 + 4n^2 + n + \frac{1}{30}}$

As with Stirling’s approximation, the relative error in Ramanujan’s approximation decreases as n gets larger. Typically these approximations are not useful for small values of n. For n = 5, Stirling’s approximation gives 118.02 while the exact value is 120. But Ramanujan’s approximation gives 120.00015.

Here’s an implementation of the approximation in Python.

    def ramanujan(x):
        fact = sqrt(pi)*(x/e)**x
        fact *= (((8*x + 4)*x + 1)*x + 1/30.)**(1./6.)
        return fact

For non-integer values of x, the function returns an approximation for Γ(x+1), an extension of factorial to real values. Here’s a plot of the accuracy of Ramanujan’s approximation.

plot of precision of Ramanujan's approximation

For x = 50, Ramanujan’s approximation is good to nearly 10 significant figures, whereas Stirling’s approximation is good to about 7.

Here’s a little trickier implementation.

    def ramanujan2(x):
        fact = sqrt(pi)*(x/e)**x
        fact *= (((8*x + 4)*x + 1)*x + 1/30.)**(1./6.)
        if isinstance(x, int):
             fact = int(fact)
        return fact

This code gives the same value as before if x is not an integer. But it gives exact values of factorial for x = 0, 1, 2, … 10. If x is 11 or greater, the result is not exact, but the relative error is less than 10^-7 and decreases as x increases. Ramanujan’s approximation always errs on the high side, so rounding the result down improves the accuracy and makes it exact for small integer inputs.

The downside of this trick is that now, for example, ramanujan2(5) and ramanujan2(5.0) give different results. In some contexts, the improved accuracy may not be worth the inconsistency.

Reference: On Gosper’s formula for the Gamma function

A Ramanujan series for calculating pi

Posted on 14 March 2011 by John

Ramanujan discovered the following remarkable formula for computing π:

$\frac{1}{\pi} = \sum_{n=0}^\infty {2n \choose n}^3 \frac{42n + 5}{2^{12n+4}}$

This is not the most efficient series for computing π. My next post will give a more efficient method, also based on work of Ramanujan. But the series above is interesting for reasons explained below.

Notice that the denominator of each term in the sum above is a power of 2. This means the partial sums of the series can be represented exactly in binary. We’ll see that each term in the series adds six bits precision to the sum once we’ve added enough terms.

To understand how to use this series, we need to estimate the binomial coefficient term. Stirling’s approximation shows that

${2n \choose n} \sim \frac{2^{2n}}{\sqrt{\pi n}}$

This tells us that the nth term in the series is a rational number with numerator something like 2⁶ⁿ and denominator 2¹²ⁿ⁺⁴. Therefore the nth term is on the order of 2⁻⁶ⁿ⁻⁴ and so the series converges quickly. The first three terms illustrates this:

$\frac{1}{\pi} = \frac{5}{16} + \frac{376}{65536} + \frac{19224}{268435456} + \cdots$

The error in summing up a finite number of terms is approximately the first term in the remainder, so just a few terms leads to an accurate approximation for 1/π and hence an accurate approximation for π.

To be a little more precise, when we sum the series from n = 0 to n = N, the error in approximating 1/π is on the order of the next term, 2^−6N−10. Said another way, summing up to the Nth term computes 1/π to 6N + 10 bits. For example, suppose we wanted to compute 1/π to 200 decimal places. That’s about 664 bits, and so 108 terms of the series should be enough.

We glossed over a detail above. We said that the nth term is on the order of 2⁻⁶ⁿ⁻⁴. That’s true for sufficiently large n. In fact, we can say that the nth term is less than 2⁻⁶ⁿ⁻⁴, but only for large enough n. How large? We need the denominator term (π n)^3/2 to be larger than the numerator term 42n + 5. This happens if n is at least as large as 58.

One advantage to using this series to compute π is that you could compute later blocks of bits without having to compute the earlier blocks, provided you’re interested in the bits beyond those contributed by 58th term in the series.

Related post: Two useful asymptotic series