Radim Řehůřek of Rare Technologies just posted an interview he and I did a few days ago. We mostly talk about consulting: getting started, finding work, good and bad leads, etc.
Interview
Solar power and applied math
The applied math featured here tends to be fairly sophisticated, but there’s a lot you can do with the basics as we’ll see in the following interview with Trevor Dawson of Borrego Solar, a company specializing in grid-connected solar PV systems.

JC: Can you say a little about yourself?
TD: I’m Trevor Dawson, I’m 25, born in the California Bay Area. I enjoy wood working, ceramics, soccer and travelling. I consider myself an environmentalist.
JC: What is your role at Borrego Solar?
TD: I am a Cost Reduction Analyst and I focus on applying Lean principles to identify and remove waste from both our internal processes and construction in the field. I use data to identify problems, prioritize them, and to verify the effectiveness of our solutions. I work with a variety of teams to reduce the cost or time of our projects.
Solar is a very fast-paced industry. Policy changes and technological improvements are being developed quickly and we have to respond quickly. A key function of my job is to assign measurable cost benefits to new practices and help ensure Borrego Solar continues to be an industry leader.
JC: What is your technical background and education?
TD: I graduated with a Bachelors of Science in Industrial & Systems Engineering (IE) from the University of Washington. I spent 3.5 years as an IE implementing process improvements on Boeing’s 777 Manufacturing Wing Line in Seattle, WA. I gained valuable experience in Lean, schedule optimization, design of experiments, and big data efforts. At Borrego, I get to apply those skills to help accelerate the adoption of the most time-tested, renewable energy source of all: the sun.
JC: What math, physics, or technical skills do you use every day?
TD: Addition, algebra, and simple statistics. I like to think I’ve mastered the basics. I also use a lot of my industrial engineering training to help gather and analyze data like design of experiments, time studies, and lean problem solving methodology.
I mostly work in Excel and use Power Pivot to drive large, cumbersome data into neat summary tables. Although the analysis can be a challenge, the hard work is rolling it up and presenting it in a way that is meaningful and convincing. When you’re suggesting a business decision, especially when it challenges the norm, your internal customers want to know the answer but they are equally interested in your process. For example, how does the business case change if a defined constraint or coefficient changes? The solar industry is dynamic and still maturing, so we have to be especially poised in our decision-making.
JC: What do you use much less than you expected?
TD: Calculus. I spent so much time learning calculus and even other things like differential equations but haven’t had much opportunity to apply them. However, I do think calculus taught me important practical problem solving skills and I put that to use now tackling large problems that span multiple pages.
JC: What math or technical skill do you wish you had more of or understood better?
TD: Excel programming and design. Excel rules the world, and although I was introduced to it at school, I think more intense courses should be commonplace. Regarding design, execution is the hardest part of any business decision, and design would help communicate results and suggestions much more effectively. A business needs verifiable proof that the suggested change is real and if executed will perform as predicted. This stage of verifying the effectiveness of a project could be improved with better design skills and may even reduce the amount of touch time and communications all the way through from inception to completion of a project.
JC: Anything else you’d like us to know?
TD: Go solar!
Mathematics of medical plastics
In this interview, I talk with Ray Rilling about applying mathematics to manufacturing medical plastics.

JC: Ray, could you start by saying a little about yourself?
RR: Sure. My name is Ray Rilling, and I am the Director of Technology at Putnam Plastics.
My initial training was cellular biology with an emphasis on epidemiology, but I decided to move to a more applied (and lucrative) field. I’ve been in medical plastics for the last 23 years.
When I saw that epidemiology was a crowded field, I pursued substantial amounts of additional coursework that allowed me to get into the medical engineering plastics space. In lots of ways I think this pick-and-choose approach was much better than a traditional bio-medical engineering degree would have been. It allowed me to focus on exactly what I needed to learn.
JC: Thanks. And tell me a bit about where you work.
RR: Putnam Plastics is a 30 year old medical plastics manufacturer, specializing in polymer-based medical components (i.e. plastic tubing for medical usage).
JC: I did some consulting work for a company that manufactures stents, so I imagine your companies have a few things in common. What is your day-to-day mathematical toolkit?
RR: We cross a lot of boundaries and there are many layers of computational needs. The majority of the computations are basic algebraic formulas to calculate simple things like annular tooling draw down ratios or the ultimate tensile of a tube. From there, you may find that calculating the burst pressure of a composite or may require the solving of a linear system.
The most challenging computations that we perform are for our complex polymer extrusion tools. These are based on Computational Fluid Dynamics (CFD) and Finite or Boundary Element Methods (FEM / BEM). Many complexities emerge because polymer flow is compressible, non-isothermal, and viscoelastic in nature. It does not allow us to use conventional Navier-Stokes or other common equations. In all reality, we rely on proprietary equations to point us in the right direction. No model has ever provided a perfect solution. We combine our experience and expertise with the applied calculations.
The most complex of the computations are performed with third party software packages and often require the use of complex meshing, materials testing for inputs, and can even require us to create modified code to suit the specific application. We work with some very creative minds and there is never a shortage of new challenges.
Aside from the design engineering mathematics, we think statistically about our results. This can be to analyze the process capability, equivalency, and even product risk analysis. This statistical analysis can be intertwined with the design engineering aspects and deal with a range of biological and medical constants (i.e. devices might need to handle liquid nitrogen or remain in bodies for years or decades).
One of my mentors used to say, “The best equation is teamwork.” Teamwork is a sort of expectation, a crowd-sourced form of expert opinion. It allows you bring a focus on what the real variables are.
Some calculations can take weeks, so having a good appreciation of how to approach the challenge is important. You can get away with not knowing what’s under the hood. But that’s dangerous. It is much better to get things done more quickly, and with better understanding. Especially when a client is waiting on results.
JC: What is some math you wish you learned more of?
Vector and tensor-based physics. As the bar in the medical device industry increases, so do the expectations of the products that we make. Being able take large number of variables or inputs and transform them into a workable model is extremely valuable. My dream is to be able to reliably calculate extrusion tooling, product failure modes, and performance properties before I start cutting steel. But in our time and age, we still rely on some development iterations and calculate what we can.
I also wish I had more applied materials science. When I am developing something in the lab, sometimes the product does not perform the way you want it to. Everytime I start learning something new, like applied surface chemistry or the effects of radiation on polymers, I think of 100 things that I could have done in previous projects.
JC: Did you learn any math you haven’t had much use for yet? I’ve used most of the math I learned, though sometimes there’s been a gap of twenty years between learning something and applying it.
RR: I actually use pretty much all of the math I’ve learned. But that’s likely because I was able to pick and choose because I went back and did supplemental studies. Even the epidemiology is useful.
JC: I wanted to pick up on what you said earlier about physical models. Could you say more about the interplay of physical and mathematical models at Putnan?
RR: The models are never completely right. We use them as a tool. They often fail in three key ways:
- We find additional variables we need to account for or constrain. In many cases our first attempt failed because the product did not perform properly in an unaccounted for way. At the end of the day it might take many iterations before we have all of the performance properties that are needed.
- We are translating soft or subjective numbers from physicians or engineers. A model will provide concrete numbers. It is often important to create a baseline product that can take the customers subjective description and correlate it to a model.
- We need to additionally constrain for cost effectiveness (i.e. minimize the amount of expensive wire in a catheter).
Those three trade offs mean that we are never able to just take a model print out and run with it. There always has to be some back and forth.
JC: It’s interesting that you consider shortcomings besides inaccuracy as failures. Someone new to applying math in the real world might think of your first point but the other points. The latter two aren’t failures from an academic perspective, but they certainly are from a business perspective.
* * *
Other interviews:
- Eric Floer on weather forecast accuracy
- Sir Michael Atiyah on mathematics
- Rick Richter, CIO of Food for the Hungry
The great reformulation of algebraic geometry
“Tate helped shape the great reformulation of arithmetic and geometry which has taken place since the 1950’s.” — Andrew Wiles
At the Heidelberg Laureate Forum I had a chance to interview John Tate. In his remarks below, Tate briefly comments on his early work on number theory and cohomology. Most of the post consists of his comments on the work of Alexander Grothendieck.
* * *
JT: My first significant work after my thesis was to determine the cohomology groups of class field theory. The creators of the theory, including my thesis advisor Emil Artin, didn’t think in terms of cohomology, but their work could be interpreted as finding the cohomology groups H0, H1, and H2.
I was invited to give a series of three talks at MIT on class field theory. I’d been at a party, and I came home and thought about what I’d talk about. And I got this great idea: I realized I could say what all the higher groups are. In a sense it was a disappointing answer, though it didn’t occur to me then, that there’s nothing new in them; they were determined by the great work that had already been done. For that I got the Cole prize in number theory.
Later when I gave a talk on this work people would say “This is number theory?!” because it was all about cohomology groups.
JC: Can you explain what the great reformulation was that Andrew Wiles spoke of? Was it this greater emphasis on cohomology?
JT: Well, in the class field theory situation it would have been. And there I played a relatively minor part. The big reformulation of algebraic geometry was done by Grothendieck, the theory of schemes. That was really such a great thing, that unified number theory and algebraic geometry. Before Grothendieck, going between characteristic 0, finite characteristic 2, 3, etc. was a mess.
Grothendieck’s system just gave the right framework. We now speak of arithmetic algebraic geometry, which means studying problems in number theory by using your geometric intuition. The perfect background for that is the theory of schemes. ….
Grothendieck ideas [about sheaves] were so simple. People had looked at such things in particular cases: Dedekind rings, Noetherian rings, Krull rings, …. Grothendieck said take any ring. … He just had an instinct for the right degree of generality. Some people make things too general, and they’re not of any use. But he just had an instinct to put whatever theory he thought about in the most general setting that was still useful. Not generalization for generalization’s sake but the right generalization. He was unbelievable.
He started schemes about the time I got serious about algebraic geometry, as opposed to number theory. But the algebraic geometers classically had affine varieties, projective varieties, … It seemed kinda weird to me. But with schemes you had a category, and that immediately appealed to me. In the classical algebraic geometry there are all these birational maps, or rational maps, and they’re not defined everywhere because they have singularities. All of that was cleared up immediately from the outset with schemes. ….
There’s a classical algebraic geometer at Harvard, Joe Harris, who works mostly over the complex numbers. I asked him whether Grothendieck made much of a difference in the classical case — I knew for number theorists he had made a tremendous difference — and Joe Harris said yes indeed. It was a revolution for classical algebraic geometry too.
Related: Applied number theory
Devnology podcast interview
When I was in Amsterdam earlier this year, Daan van Berkel interviewed me for the Devnology podcast. We talked about my winding career path, the overlap of math and computing, bringing math and computing closer together, formal methods, etc.
The podcast was posted this afternoon here. [Update: Looks like the link has gone away.]
Related post: Looking like you know what you’re doing
Writing down an unwritten language
In this post I interview Greg Greenlaw, a friend of mine who served as a missionary to the Nakui tribe in Papua New Guinea and developed their writing system. (Nakui is pronounced like “knock we.”)
JC: When you went to PNG to learn Nakui was there any writing system?
GG: No, they had no way of writing words or numbers. They had names for only seven numbers — that was the extent of their counting system — but they could coordinate meetings more than a few days future by tying an equal number of knots in two vines. Each party would take a vine with them and loosen a knot each morning until they counted down to the appointed time — like and advent calendar, but without numbers!
JC: I believe you said that Nakui has a similar grammar to other languages in PNG but completely different vocabulary. Were you able to benefit from any other translation work in the area? Will your work serve as a starting point for translating another language?
GG: Yes. Missionaries had moved into our general area back in the 80’s and the languages they studied had mostly the same grammar features that we saw in the Nakui language. This sped the process, but in truth, the slowest part of learning to speak was not analyzing the grammar, it was training yourself to use it. Each Nakui verb could conjugate 300 different ways depending on person, recipient, tense, aspect, direction, and number.
JC: Do any of the Nakui speak a pidgin or any other language that served as a bridge for you to learn their language?
GG: We were blessed with one very good pidgin speaker when we moved into the village and several others who spoke the Melanesian Tok Pisin at a moderate level. That was a help in eliciting phrases and getting correction, but there were limits to how much they understood about their own speech. They had never thought about their language analytically and could not state a reason for the different suffixes used in the language, they just knew it was the right way to say something. Most peculiar was that they couldn’t even tell where certain word breaks were. Their language had never been “visible” to them. Nouns were easy to separate out, but it was hard to know if certain modifiers were affixes or separate function words.
JC: What are a few things that English speakers would find surprising about the language?
GG: Nakui has very few adjectives but innumerable verbs. They do the majority of their describing by using a very specific verb. There is a different verb for cutting something in the middle as opposed to cutting off a small section or cutting it long ways or cutting something to fall downward or cutting something to bits. The correct verb for the situation will also depend on the object being cut — is it log-like, leaf-like, or flesh-like.
JC: Do you try to learn a new language aurally first before starting on a writing system, or do you start developing a writing system early on so you can take notes?
GG: It’s language, so you always want your ears and tongue to lead your eyes. We use the international phonetic alphabet to write down notes, but we encourage language learners to hold off on writing anything for almost a month. After they are memorizing and pronouncing correctly a host of nouns and some noun modifiers, then we encourage them to start writing down their data with the phonetic alphabet. About half way to fluency they usually have enough perspective on the variety of sounds and where those sounds occur that they can narrow down a useful alphabet.
JC: How long did it take to learn the language? To create the writing system? How many people were working on the project?
GG: Primarily Tim Askew and myself, but there were three other missionaries that worked among the Nakui in the early days and each had some contribution to our understanding. The biggest credit really belongs to God, by whose grace we were allowed to live there and by whose strength we were able to chip away for three years until the job was done.
JC: Can you describe the process you went through to create the writing system?
GG: Well after collecting thousands of words written phonetically we could start a process of regularizing all that data. Looking at the language as a whole we had to decided the sleekest, most uniform way to consistently spell those sounds phonetically. After cleaning up our data we could take a hard look at which of the sounds were unique and which are just modified by surrounding sounds. Phonetically the English language has three different ‘t’ sounds: an aspirated ‘t’, and unaspirated ‘t’, and an unreleased ‘t’. We only think of one ‘t’ sound, though, and it would be confusing (and irritating) if we had three ‘t’ symbols in our alphabet. Our ‘t’s just become unreleased automatically when they are at the end of a word and they become unaspirated when they blend with an ‘s’. You need to narrow down the number of sounds to just the ones that are significant and meaningful. It is only those unique sounds that are given letters in the alphabet.
JC: What is the alphabet you settled on? Do the letters represent sounds similar to what an English speaker would expect?
GG: We found 10 vowel sounds and 10 consonant sounds were needful in the Nakui language. The 10 consonants are symbolized the same as English, but the vowels had to be augmented. We borrowed the letter ‘v’ to become the short ‘u’ sound and used accent marks over other vowels to show their lowered and more nasalized quality.
JC: Could you give an example of something written in Nakui?
GG: This is John 3:16. Músvilv Sisasvyv me iyemvi, “Kotvlv asini niyanú nonú mvli mvlei ufau. Múmvimvilv, tuwani aluwalv siyv tuwayv itii, asinosv. Mvimeni notalv me svmvleliyelv, ‘Sisasvni yáfu kokuimvisv,’ múmeni nonv ba itinvini, i tínonvminvini.
JC: Is it unusual for a language to have as many vowel symbols as consonant symbols?
GG: Good question. I’m not sure what normal would be worldwide, but I know we have a lot more than five vowel sounds in English! All our English vowel symbols have double or triple allophones (long sounds, short sounds, alternate sounds) making it very challenging to instruct my 6 yr old in the skill of reading.
JC: Have you published anything on your work, say in a linguistics journal?
GG: No, there is nothing unique in what we did. Truth is, we organized our findings and reported our work in an informal, non-academic, pragmatic way because our goal was not a PhD in anthropology, but a redeeming ministry in the lives of tribal men and women and ultimately a commendation from the Maker of men.
JC: How many of the Nakui can read their language?
GG: All the young men in our village are readers now, with the exception of a dyslexic man who attempted our literacy course three times without result. About 1/3 of the young women can read. They have less available time for study, and in the early days the village leaders did not allow the girls to be in class with the boys. As a result, literacy for ladies had a slower start and fewer participants. There were older men who tried to learn to read, but none that succeeded. The gray matter seemed to have stiffened.
JC: If English didn’t have a writing system and you were designing one from scratch, what would you do differently?
GG: Wow, we have six kids we’ve taught to read – we would do a lot differently! The ideal is to have one symbol for each meaningful sound in the language. English would need more vowels and fewer consonants. Life would actually be more pleasant without ‘c’, ‘j’, ‘q’ and ‘x’. If you removed those and added about six vowels we could come up with a spelling system that was predictable and easy to learn.
JC: Anything else you’d like to say?
GG: One of the most remarkable things about the Nakui language is how sophisticated and complex it is. Unblended with other languages, it is extremely consistent in its grammar. Although it is in a constant state of change (rapid change relative to written languages of the world), it remains organized. This order is not to the credit of the society that speaks it, it happens utterly in spite of them. They are completely unaware of the structure of their own grammar and are perhaps the most disorderly people on the planet. The aspects of life over which they hold sway are corrupt and miserable, but in this small, unmanaged area of their lives, a glimpse of the divine still peeks out. The God of order, who created them in His own image, gave them an innate ability to communicate complex ideas in and orderly way. Like Greek, they specify singular, dual and plural. They have six tenses (English has only three), and 11 personal pronouns (English has only six). Every verb is conjugated to carry this specificity with extreme consistency. The verb to ‘go’ is the only irregular verb in the whole Nakui language. English, although vast, is a disheveled mess compared to what is spoken by these stone age people in the swamps of interior New Guinea.
Related posts
Audio of Atiyah interview
Interview with Sir Michael Atiyah
Yesterday I had the privilege of interviewing Sir Michael Atiyah. We talked about mathematical writing, the interplay of abstraction and application, and unified theories of physics. A shorter excerpt, focusing on mathematical exposition, appears on the HLF conference blog.
Update: I’ve posted the audio of the interview here.

Photo by Bernhard Kreutzer
JC: I ran across your expository papers when I was a student and very much enjoyed reading them. Two things stood out that I still remember. One was your comment about one-handed pottery, that the person creating it might be very proud of what he was able to do with only one hand, but the user of the pottery doesn’t care.
MA: That was my response to the kind of highly technical mathematics that showed you could do something under extremely minimal hypotheses, but who cares? Sometimes its useful, but often its for the benefit of the technicians and not the general user.
JC: The other thing I remember from your papers was your rule that exposition should proceed from the particular to the abstract.
MA: I have strong views on that. Too many people write papers that are very abstract and at the end they may give some examples. It should be the other way around. You should start with understanding the interesting examples and build up to explain what the general phenomena are. This was you progress from initial understanding to more understanding. This is both for expository purposes and for mathematical purposes. It should always guide you.
When someone tells me a general theorem I say that I want an example that is both simple and significant. It’s very easy to give simple examples that are not very interesting or interesting examples that are very difficult. If there isn’t a simple, interesting case, forget it.
One feature of mathematics is its abstraction. You can encompass many things under one heading. We talk about waves. For us a wave is not a water wave, it’s an oscillating function. It’s a very useful concept to extract things out.
Mathematics is built on abstractions. On the other hand, we have to have concrete realizations of them. Your brain has to operate on two levels. It has to have abstract hierarchies, but it also has to have concrete steps you can put your feet on.
Everything useful in mathematics has been devised for a purpose. Even if you don’t know it, the guy who did it first, he knew what he was doing. Banach didn’t just develop Banach spaces for the sake of it. He wanted to put many spaces under one heading. Without knowing the examples, the whole thing is pointless. It is a mistake to focus on the techniques without constantly, not only at the beginning, knowing what the good examples are, where they came from, why they’re done. The abstractions and the examples have to go hand in hand.
You can’t just do particularity. You can’t just pile one theorem on top of another and call it mathematics. You have to have some architecture, some structure. Poincaré said science is not just a collection of facts any more than a house is a collection of bricks. You have to put it together the right way. You can’t just list 101 theorems and say this is mathematics. That is not mathematics. That is categorization. Mathematics is not a dictionary.
JC: I think someone called that stamp collecting or bug collecting.
MA: Yes. Rutherford was very scathing about chemistry. He said there is Schrodinger’s equation, and everything else was cookery.
JC: I think people are more willing to give these examples verbally than in print.
MA: You’re quite right. It is kind of a reaction in recent times. People began to go beyond what they could prove and got a bit woolly and they got a bad reputation, like some of the Italian algebraic geometers. So you are taught to be rigorous, and you learn to be very, very rigorous. And then you think that your papers have to be ultra-rigorous, otherwise the guys behind you will find fault with what you’re saying. The need for rigor, it’s a bit like the people who are afraid of being sued by the lawyers. If you don’t put it down, 100%, someone will sue you! People cover themselves in advance, but the result is an unreadable paper.
But when you talk like this, you’re allowed to lower the level of rigor in order to increase the power of explanation. You can explain things using hand waving, use analogies, leaving out technical details, because you want to get the idea across. But when people write, particularly mathematics, and particularly in the last decades of the last century, people became very formalistic. Papers were rejected if they were not rigorous enough. People were reacting to the loose talk of the past. So we went to the other extreme. And most papers aren’t read. That’s a theorem! Someone said the average number of readers of a paper is one, and that’s the author.
JC: And with multiple authors, maybe it’s a fraction.
MA: That’s right. I used to tell people, make your introduction understandable to a general mathematician. Don’t get into the technicalities there. Say you’ll deal with them later. Don’t just say “Let X be a space” and jump into the details but that’s what people do. So you’re right. But people know when they give a lecture to behave differently, they can use all the tools of hand-waving, literally! [waves hands], to get idea across.
Some people write so well it’s as good as a lecture. Hermann Weyl is my great model. He used to write beautiful literature. Reading it was a joy because he put a lot of thought into it. Hermann Weyl wrote a book called The Classical Groups, very famous book, and at the same time a book appeared by Chevalley called Lie Groups. Chevalley’s book was compact, all the theorems are there, very precise, Bourbaki-style definitions. If you want to learn about it, it’s all there. Hermann Weyl’s book was the other way around. It is discursive, expansive, it’s a bigger book, it tells you much more than need to know. It’s the kind of book you read ten times. Chevalley’s book you read once. You go back to these other books. They’re full of throw-away lines, insights that are not fully relevant for going from A to B. He’s trying to give you a vision for C. Not many people write like that. He was an exception.
In the introduction he explains that he’s German, he’s writing in a foreign language, he apologizes saying he is writing in a language that was “not sung by the gods at my cradle.” You can’t get any more poetic than that. I’m a great admirer of his style, of his exposition and his mathematics. They go together.
JC: I ran across an old paper by Halmos recently where he refers to your index theorem as a pinnacle of abstraction, and I thought about the comparison with Shinichi Mochizuki’s claimed proof of the abc conjecture. The index theorem rests on a large number of abstractions, yet these are widely shared abstractions. Mochizuki’s proof also sits on top of many abstractions, but nobody understands it.
MA: These problems have a long history. The past is part of your common heritage. They generalize classical theorems. They go step by step through abstractions. Everybody knows what they’re for. So there’s a big pyramid. The base is very firm. The purpose of abstraction is that you can go back down to earth and apply it here or apply it there. You don’t just disappear in the clouds. You walk along the ridge and go down to this valley or that.
JC: Maybe the proof of the abc conjecture is more of a flag pole than a pyramid.
MA: And when you get to the top of a flag pole, what do you do? You could be like the hermit saints who would sit on a pillar. …
JC: I saw a video recently of a talk you gave a couple years ago in which you described yourself as a “mystic,” someone hoping for a unification of several diverse theories of physics.
MA: That’s right. I was saying that there are these different schools of thought, each with a prophet leading them. I wanted to say that I didn’t follow any one of them, that you can search for the truth through many different ways. The mystic thinks there’s a little bit of truth in everybody’s line. I think every interesting line has something to be said for it.
There are the string theorists, that’s the biggest school, and people like Roger Penrose, Alain Connes, … They all have strong ideas, and they attract a certain group of followers. These are serious people, there’s serious reason to believe what they’re doing, and there’s something in it. Bridges have been built between these theories. They’ve found unexpected links between them. So that’s already a bit of convergence. So I’m hoping there will be more convergence, using the best of each theory.
It would be sad if we’ve seen the last of the visions of the prophets. It would be sad if new fundamental insights were no more. There’s no reason it should stop. At the end of the 19th century people thought physics was finished. We know absolutely everything, but at the beginning of the 20th century it exploded. There’s no reason not to think there will be further revolutionary ideas emerging. Any day, any time, anywhere.
I’m an optimist. I believe in new ideas, in progress. It’s faith. I’ve recently been thinking about faith. If you’re a religious person, which I’m not, you believe God created the universe. That’s why it works, and you’re trying to understand God’s works. There are many scientists who work in that framework. Scientists, outside of religion, have their own faith. They believe the universe is rational. They’re trying to find the laws of nature. But why are there laws? That’s the article of faith for scientists. It’s not rational. It’s useful. It’s practical. There’s evidence in its favor: the sun does rise every day. But nevertheless, at the end of the day, it’s an article of faith.
I gave a talk about Pythagoras. Bertrand Russell said that Pythagoras was probably the most influential philosopher who ever existed, because he was the first person to emphasize two things, the role of numbers in general, and the role of numbers in music in particular. He was so struck by this that he believed numbers were the base of the universe. He was the first person to articulate the view that the universe is rational, built on rational principles.
JC: What do you think of category theory? Do you think it plays a role in this grand unification?
MA: Well, I’m a conservative in many ways. As you get older you get more conservative. And I don’t believe in things unless I’m convinced of their utility. Ordinary categories are a useful language. But it’s become now more formal. There are things called 2-categories, 3-categories, building categories on categories. I’m now partially converted. I think it may be necessary. Algebra was an abstraction when it first came along. Then you get into categories and higher levels of abstraction. So I’m broad minded about it, but I’d like to be persuaded.
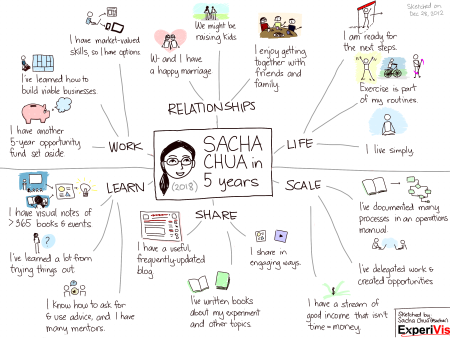
Interview with Sacha Chua
I spoke with Sacha Chua last week. We talked about entrepreneurship, Emacs, having eclectic interests, delegation, and more.

J: I ran into you by searching on Emacs topics. When I look at your blog, I see that you do a lot of interesting things, but it’s a little hard to get a handle on exactly what you do.
S: Oh, the dreaded networking quirky question. What exactly do you do?
J: Yeah, people have said the same thing to me. Not to put you in a box, but I was curious. I see from your site that you do graphic art—sketching and such—and it doesn’t create the impression that you’re someone who would spend a lot of time in front of Emacs. So I’m curious how these things fit together, how you got started using Emacs and how you use it now.
S: So my background is actually fairly technical. I’ve been doing computer programming for ages and ages. In high school I came across a book Unix Power Tools, which is how I got interested in Emacs. And because I was interested in programming, in open source, a little bit of wearable computing as well, I got to know Emacs and all these different modules it had. For example, Emacspeak is amazing! It’s been around since the 1990s and it’s a great way to use the computer while you’re walking around. Because I love programming and because I wanted to find a way to help out, I ended up maintaining PlannerMode and later EmacsWiki mode as well.
When I went to university, I took up computer science. After I finished, I taught. Then I took my masters in Toronto, where I am now. Emacs was super helpfu;—being able to do everything in one place. After I finished my masters, I did a lot of software consulting with IBM. I did business consulting as well. Then in 2012, after saving up, I decided to go on pretty much the same adventure you’re on. I’m completely unhirable for the next five years! Most businesses struggle for the first five years, so I saved up enough to not worry too much about my expenses for the next five years. I’m one year in, four years to go, and that’s where I am.
At networking events, I like to shake people up a bit by telling them I’m semi-retired. I’m in this five-year experiment to see how awesome life can be and what I can do to make things better. I’ve done technical consulting, business consulting, sketching, illustration, writing, all sorts of things. Basically, my job description is context-dependent.
J: I understand that.
S: I use Emacs across all the things I do. When I’m doing technical and business consulting, I use Emacs to edit code, to draft documents, even to outline comic strips. And when I’m doing illustration, Emacs—especially Org Mode—helps me keep track of clients and deliverables, things to do, agenda, calendar, deadlines.
J: I’m basically running my life through Org Mode right now. When you say you use Emacs to draft documents, are you using LaTeX?
S: I used LaTeX when I was working on my master’s thesis and other papers, I think. Now I mostly use org mode and export from there.
J: Are you using Emacs for email?
S: I used to. But I’m stuck on Windows to use drawing programs like Sketchbook Pro on my Tablet PC. So it’s harder to set up my email like I had it set up when I used Ubuntu. Back when I used Ubuntu, I was very happy with Gnus.
J: Do you work entirely on Windows, or do you go back and forth between operating systems?
S: I have a private server that runs Linux. On Windows I run Cygwin, but I miss some of the conveniences I had when I had a nicely set-up Linux installation.
J: When you’re running Emacs on Windows, I’m sure you run into things that don’t quite work. What do you do about that?
S: Most things work OK if they’re just Emacs Lisp, but some things call a shell command or use some library that hasn’t been ported over yet. Then I basically wail and gnash my teeth. Sometimes I get things working by using Cygwin, but sometimes it’s a bit of a mess. I don’t use Emacs under Cygwin because I prefer how it works natively. I don’t run into much that doesn’t work.
J: So what programming languages do you use when you’re writing code?
S: I do a lot of quick-and-dirty things in Emacs Lisp. When I need to do some XML parsing or web development, I’ll use Ruby because a lot of people can read it and there are a lot of useful gems. Sometimes I’ll do some miscellaneous things in Perl.
I love doing programming and putting together tools. And I quite enjoy drawing, helping people with presentation and design. So this is left brain plus right brain.
It does boggle people that you can have more than one passion, but others are, like, “Yeah, I know, I’m like that too.”
J: I think having an interest in multiple things is a healthier lifestyle, but it’s a little harder to market.
S: Actually, no. I finally figured out a name for my company, ExperiVis, after a year of playing with it. People reach out to me and we figure out whether it’s a good fit. I don’t need to necessarily guide people to just this aspect or another of my work. I like the fact that people bump into these different things.
J: When we scheduled this call, I went through your virtual assistant. How do you use a virtual assistant?
S: One of the things I don’t like to do is scheduling. I used to get stressed out about scheduling when I did it myself. I’ve always been interested in delegating and taking advantage of what other people enjoy and are good at. I work with an assistant—Criselda. She lives in the Philippines. I found her on oDesk. She works one to four hours a week, more or less, and keeps track of her time.
J: What else might you ask a VA to do?
S: I’ve asked people to do web research. I’ve had someone do a little bit of illustration for me. I’ve had someone do a little bit of programming for me because I want to learn how to delegate technical tasks. He does some Rails prototyping for me. I have someone doing data entry and transcription. It’s fascinating to see how you can swap money for time, especially for things that stress me out, or bore me, or things I can’t do.
Every week I go over my task list with my VA to see which of the tasks I should have delegated. Still working on it!
* * *
Later on in the conversation Sacha asked about my new career and had this gem of advice:
Treating this as a grand experiment makes it much easier for me to try different approaches and not be so scared, to not treat it as a personal rejection if something doesn’t work.
Related post: People I’ve interviewed and people who have interviewed me
Interview with Michael Hammel, author of The Artist’s Guide to GIMP
Michael J. Hammel is the author of The Artist’s Guide to GIMP, a book I reviewed three weeks ago. The following interview is based on my correspondence with Michael.
JC: The bio on your book says that you are an embedded software developer. Is GIMP something you use for fun or is it related to your work? Was it related to your work before?
MH: I use it once in awhile at work but not often. GIMP started as something related to what I worked on when it first came out (graphics software for Unix systems). But I’ve never been paid to be an artist. At one point I looked at trying to use what I knew about it to leverage my way into Pixar or Dreamworks. But that never panned out and my interest in that kind of animation has peeked and ebbed, mostly because I decided I didn’t want to live in California (too expensive).
JC: How did you become involved in the development of GIMP?
MH: When GIMP was born, back around 1995 or so, I was working for a company that provided commercial X servers for Unix systems (Xi Graphics, started by Thomas Roell who wrote the original reference implementation of an X server for 386 systems, aka X386, which begot XFree86 which begot X.org). I packaged Motif as part of my work. A guy I worked with noticed GIMP’s Motif version and pointed me at it. I wrote a plugin for John Beale’s sparkle code (the original Sparkle plugin). I’ve been working with GIMP ever since.
JC: Are you still a developer for GIMP or primarily a user?
MH: A user. I haven’t provided any useful code development to the project in quite sometime.
JC: What’s it like to be a developer on GIMP?
MH: Take this with a grain of salt. It’s a follower’s view from the outside, without being involved with the developers directly.
GIMP’s developer community is somewhat different than other open source communities that I’ve been involved with. GIMP’s leadership is de facto, but not necessarily structured. Many other projects have defined leaders with defined tasks. GIMP’s development is a little more oriented towards scratching your own itch: pick something that that you want to improve and start working on it. The only tough part (at least for some) is understanding and adhering to the main developers coding styles and rules, which are not (to my knowledge) written down.
My only complaint with this style is it tends to allow long term development cycles. End users can’t rely on when new features might be available. While the developers want do things “the right way”, that means that users have been waiting a very long time, for example, for deep paint support. There is a tradeoff for how you do development. Remember that the developers are volunteers, so there is no valid reason for complaining if you, as a user, aren’t getting what you want when you want it. If it bothers you, step in and help out. Otherwise, do as I do: be content with their development process.
JC: What advice would you give people who want to learn image editing?
MH: I learned how to use GIMP by reading Photoshop texts. Image editing is a common set of processes. Think about what you want to do if you weren’t using software. You’re house needs a new color? You mask off the window boarders and roof line and start painting. Same thing in image editing. Only difference: it’s easier to try different colors. Image editing is all about selections and masks. I’m not talking about creating the next Marvel comic, I mean editing existing images. Once you identify what needs to be changed using a selection and mask, you can do all kinds of things: copy and distort, recolor, refocus, etc.
Making comics or custom drawings requires real artistic talent to create a rough design on paper, then import (via scanner or digital camera) into GIMP for cleanup and coloring.
Personally, I prefer taking photos and mixing them together to create a scene that otherwise wouldn’t exist. There is a small example of this in the book. A photo of a city skyline as it exists and a munged version I created to make the city look decayed and falling apart. Beats me what people think of that image, but the creative process that went into it was very relaxing.
JC: What advice would you give people who want to learn GIMP in particular?
MH: Buy my book. Seriously. You learn both at the same time: what is image editing and how do you do it with GIMP. GIMP is just like any other desktop software. You learn where the menus are and what the various windows provide. The rest of your time is learning process — creating a workflow to produce a specific image type or style.
JC: What other software do you use/recommend for creating graphics?
MH: I use simple viewers like Geeqie for browsing images, but if you’re into photography you’ll nee something like f-spot. Photographers, who are nuts about image quality, should learn ufraw. Those interested in 3D or animation should take a look at Blender.
JC: Do you want to say anything about your work with embedded development?
MH: It’s my primary focus in life these days. I’m working on creating a custom media-focused Linux distribution (which I call BeagleBox) for the BeagleBoard C4 (and later the xm). I’d like to get my hands on the Raspberry Pi but wasn’t able to place an order when they first went on sale.
Embedded work is the future for Linux. The desktop for non-techies might change to tablets or such, but Linux will be in everything: your fridge, your TV, your car, your electrical system, your water and sewage systems, your phone, you’re neighbors who are flying robotic UAVs to peek in your windows. Everything.
My day job is building a radar system for UAVs (the big ones) that use embedded Linux to run out of flash. But the direction of interest is smaller devices, little boards with processors and memory in one, like the Pi or BeagleBoard, that can sense the environment and communicate to the rest of the household, with one of those devices used to display all the info on a big wall, removing the need for specialized devices just for the purpose of display.
Anyway, I’m really into making my own custom distribution based on Crosstool-NG (for cross compiling), u-boot (bootloader), Buildroot/Busybox (for root filesystems) and of course Linux.