Zcash price doubled

Posted on by John

My interest in cryptocurrency is primarily technical, and privacy coins are the most technically interesting. The math behind coins like Monero and Zcash is far more sophisticated than the math behind Bitcoin.

I’m also interested in the privacy angle since I work in data privacy. The zero-knowledge proof (ZKP) technology developed for and tested in privacy coins is applicable outside of cryptocurrency.

I don’t follow the price of privacy coins, but I heard about the price of Zcash doubling recently.

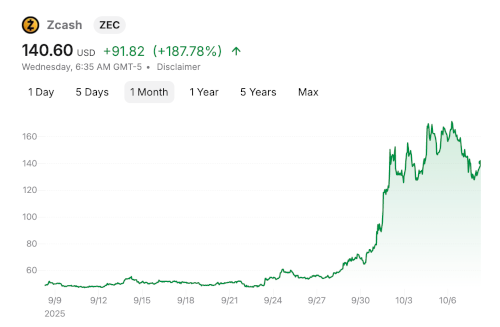
I’d like to understand why that happened, especially why it happened so suddenly, though I’m very skeptical of post hoc explanations of price changes. I roll my eyes when I hear reporters say the stock market moved up or down by some percent because of this or that event. Any explanation for the aggregate behavior of a complex system that fits into sound byte is unlikely to contain more than a kernel of truth.

Naval Ravikant said on October 1

Bitcoin is insurance against fiat.
ZCash is insurance against Bitcoin.

This was after Zcash had started rising, so Naval’s statement wasn’t the cause of the rise. But the idea behind his statement was in the air before he crystalized it. Maybe the recent increase in the price of Bitcoin led to the rise of Zcash as a hedge against Bitcoin falling. It’s impossible to know. Traders don’t fill out questionnaires explaining their motivations.

It has been suggested that more people are interested in using Zcash as a privacy-preserving currency, not just buying it for financial speculation. It’s plausible that this could be a contributing factor in the rise of Zcash, though interest in financial privacy is unlikely to spike over the course of one week, barring something dramatic like FDR’s confiscation of private gold in 1933.

The price of Monero increased along with Zcash, though not as by nearly as much.

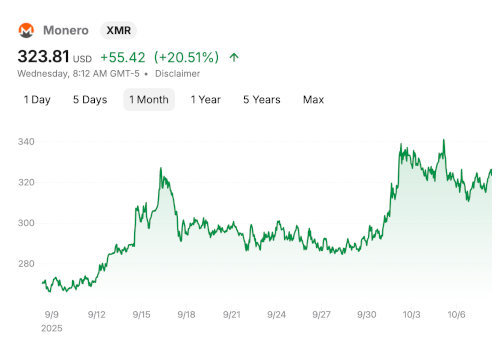
This suggests there may be increased interest in privacy coins more generally and not just in Zcash.

It would be interesting to see how people are using Zcash and Monero—how much is being spent on goods and services and how much is just being traded as an investment—but this would be difficult since privacy coins obscure the details of transactions by design.

Related posts

RSA with multiple primes

Posted on by John

Typically RSA public keys are the product of two large primes, n = pq. But there’s no reason they couldn’t be the product of say three primes, n = pqr, or more primes, as long as φ(n), or λ(n), is calculated correctly.

Encryption is done the same way. Decryption could be done the same way, except there is the opportunity for it to be more efficient. The trick is to use the CRT (Chinese Remainder Theorem) in a way similar to Garner’s algorithm. This is why RSA with multiple primes is sometimes used for digital signatures.

The difficulty of factoring n using the GNFS algorithm doesn’t change depending on the number of factors n has, as long as all the factors are sufficiently large, far too large to find using trial division.

Daniel Bernstein’s post-quantum RSA paper was based on keys that are the product of a large number of 4096-bit primes. This way all the arithmetic is carried out modulo 4096-bit primes, not modulo terabyte primes.

True growth rate accounting for inflation

Posted on by John

In an inflationary economy, the purchasing power of your currency continually deteriorates. If you have an investment that grows slower than your purchasing power shrinks, you’re actually losing value over time. The true rate of growth is the rate of change in the purchasing power of your investiment.

If the inflation rate is r and the rate of growth from your investment is i, then intuitively the true rate of growth is

g = i − r.

But is it? That depends on whether your investment and inflation compound periodically or continuously [1].

Periodic compounding

If you start with an investment P, the amount of currency in the investment after compounding n times will be

P(1 + i)n.

But the purchasing power of that amount will be

P(1 + i)n (1 + r)−n.

If the principle were invested at the true rate of growth, its value at the end of n periods would be

P(1 +  g)n.

So setting

P(1 + i)n (1 + r)−n = P(1 +  g)n

gives us

g = (i − r) / (1 + r).

The true rate of growth is less than what intuition would suggest. To achieve a true rate of growth g, you need i > g, i.e.

i = g + rg + r.

Continuous compounding

With continuous compounding, an invent of P for time T becomes

P exp(iT)

and has purchasing power

P exp(iT) P exp(−rT).

If

P exp(iT) P exp(−rT) = P exp(gT)

then

g = i − r

as expected.

So what?

It’s mathematically interesting that discrete and continuous compounding work differently when inflation is taken into account. But there are practical consequences.

Someone astutely commented that inflation really compounds continuously. It does, and not at a constant rate, either. But suppose we find a value of the monthly inflation rate r equivalent to the true annual rate. And suppose you’re in some sort of contract that pays monthly interest i. Then your true rate of growth is (i − r) / (1 + r), not (i − r).

If r is small, the difference between (i − r) / (1 + r) and (i − r) is small. But the larger r is, the bigger the difference is. As I’ve written about before, hyperinflation is counterintuitive. When r is very large, (i − r) / (1 + r) is much less than (i − r).

Related posts

[1] Robert C. Thompson. The True Growth Rate and the Inflation Balancing Principle. The American Mathematical Monthly, Vol. 90, No. 3 (Mar., 1983), pp. 207–210

A quiet change to RSA

Posted on by John

An RSA public key is a pair of numbers (e, n) where e is an exponent and n = pq where p and q are large prime numbers. The original RSA paper said choose a private key d and compute e. In practice now we choose e and compute d. Furthermore, e is now almost always 65537 for reasons given here. So the public key is essentially just n.

Euler’s totient function

The relationship between the exponent and the private decryption key in the original RSA paper was

ed = 1 mod φ(n).

It is easy to compute e given d, or d given e, when you know Euler’s totient function of n,

φ(n) = (p − 1)(q − 1).

The security of RSA encryption rests on the assumption that it is impractical to compute φ(n) unless you know p and q.

Carmichael’s totient function

Gradually over the course of several years, the private key d changed from being the solution to

ed = 1 mod φ(n)

to being the solution to

ed = 1 mod λ(n)

where Euler‘s totient function φ(n) was replaced with Carmichael‘s totient function λ(n).

The heart of the original RSA paper was Euler’s generalization of Fermat’s little theorem which says if a is relatively prime to m, then

aφ(n) = 1 (mod n)

Carmichael’s λ(n) is defined to be the smallest number that can replace φ(n) in the equation above. It follows that λ(n) divides φ(n).

Why the change?

Using Carmichael’s totient rather than Euler’s totient results in smaller private keys and thus faster decryption. When n = pq for odd primes p and q,

λ(n) = lcm( (p − 1), (q − 1) ) = (p − 1)(q − 1) / gcd( (p − 1), (q − 1) )

so λ(n) is smaller than φ(n) by a factor of gcd( (p − 1), (q − 1) ). At a minimum, this factor is at least 2 since p − 1 and q − 1 are even numbers.

However, an experiment suggests this was a trivial savings. When I generated ten RSA public keys the gcd was never more than 8.

from sympy import randprime, gcd

for _ in range(10):
    p = randprime(2**1023, 2**1024)
    q = randprime(2**1023, 2**1024)
    print(gcd(p-1, q-1))

I repeated the experiment with 100 samples. The median of the gcd’s was 2, the mean was 35.44, and the maximum was 2370. So the while gcd might be moderately large, but it is usually just 2 or 4.

Better efficiency

The efficiency gained from using Carmichael’s totient is minimal. More efficiency can be gained by using Garner’s algorithm.

Fermat primes and tangent numbers

Posted on by John

Fermat numbers

The nth Fermat number is defined by

F(n) = 2^{2^n} + 1

Pierre Fermat conjectured that the F(n) were prime for all n, and they are for n = 0, 1, 2, 3, and 4, but Leonard Euler factored F(5), showing that it is not prime.

Tangent numbers

The nth tangent number is defined by the Taylor series for tangent:

\tan(z) = \sum_{n=0}^\infty T(n) \frac{z^n}{n!}

Another way to put it is that the exponential generating function for T(n) is tan(z).

Fermat primes and tangent numbers

Here’s a remarkable connection between Fermat numbers and tangent numbers, discovered by Richard McIntosh as an undergraduate [1]:

F(n) is prime if and only if F(n) does not divide T(F(n) − 2).

That is, the nth Fermat number is prime if and only if it does not divide the (F(n) − 2)th tangent number.

We could duplicate Euler’s assessment that F(5) is not prime by showing that 4294967297 does not divide the 4294967295th tangent number. That doesn’t sound very practical, but it’s interesting.

Update: To see just how impractical the result in this post would be for testing whether a Fermat number is prime, I found an asymptotic estimate of tangent numbers on OEIS,  and estimated that the 4294967295th tangent number has about 80 billion digits.

[1] Richard McIntosh. A Necessary and Sufficient Condition for the Primality of Fermat Numbers. The American Mathematical Monthly, Vol. 90, No. 2 (Feb., 1983), pp. 98–99

Memorizing a list of seed words

Posted on by John

If you need to memorize a list of up to eight words, particularly for a short period of time, the most efficient method may be brute force: rehearse the words in sequence until you can remember them. But if you need to remember more words, or remember the list for a longer time, some sort of peg system would be better.

Pegs

A peg system begins with a list of images firmly associated with integers. You drill these associations into your brain like driving pegs into wood, then “hang” things on the pegs.

The choice of pegs could be arbitrary, but it’s easier to acquire a set of pegs if there’s some pattern to them, such as the Major system. An example set of pegs based on the Major system follows.

  1. tea
  2. Noah
  3. ammo
  4. arrow
  5. law
  6. show
  7. key
  8. ivy
  9. pie
  10. toes
  11. toad
  12. dune

and so on.

Learning a set of pegs is harder than hanging things on the pegs. But once you have a peg system, you can reuse it for many different things.

Numbered lists

Here’s something I resisted but eventually came to accept: it’s easier to memorize a numbered list than an unnumbered list. For example, it’s easier to learned a numbered list of the US presidents—#1 Washington, … #16 Lincoln, … etc.—than to simply learn to recite the list.

This is counterintuitive because it requires memorizing more information. But the key is this: with a numbered list, you only have to remember pairs of pegs and items. To memorize a list of 100 items, you don’t have to memorize a sequence of 100 things; you have to remember a set of 100 pairs. If you forget an item, you forget one item: it doesn’t throw off anything else. It’s also easier to review and test yourself on a numbered list.

I’ve noticed when journalists are reporting on some memory stunt, they’ll say something like “Not only can he recite the Fortune 500, he could pull up each one by number.” Reading between the lines, this person used a peg system. He memorized each company with its number, not to make things harder, but to make things easier.

Seed phrases

A seed phrase for a crypto wallet is a list of 12 to 24 words. You could memorize a list of 12 words by rote without too much effort, but a list of 24 would be more than twice as hard. Since you want to remember wallet seed words for a long time, and there are potentially huge consequences to forgetting part of the list, I’d recommend a peg system.

To create an example, I chose 12 words by sampling the BIP39 word list with replacement using the command

    shuf -n 12 -r english.txt

This returned the following words:

  1. entry
  2. lava
  3. foot
  4. vibrant
  5. diet
  6. pulp
  7. canal
  8. name
  9. noble
  10. dream
  11. breeze
  12. bar

This probably isn’t a valid wallet address, but it’s like one [1].

To memorize the list using the pegs above, you would create mental images associating tea with entry, Noah with lava, ammo with foot, etc. You might imagine Noah’s ark on a sea of lava, or shooting yourself in the foot.

Noah's ark floating on lava

As I’ve written before, some of the BIP39 seed words are less than ideal for memorization. Lava creates a vivid mental image; entry does not. Maybe you could change entry to entryway, imagining a giant teapot in the entryway to your house.

The BIP39 words are uniquely determined by their first four letters. You could change the words if you like, as long as you keep the initial letters the same. For example, if you tried to type entryway into a wallet, autocomplete would kick in after you typed entr and so the rest of the letters don’t matter.

Recall

To recall the list, you go down your list of pegs and see what is associated with each. This is why pegs have to be unique. If you want to encode a number using the Major system, you can encode the same digits different ways at different times. For instance, maybe you encode 12 as Dune one time and Athena the next. But when recalling a list, you need to recall the peg for a number and recall what it’s associated with.

Related posts

[1] The seed words come from a list of 2048 words, so each word carries 11 bits, so 12 words encode a 128-bit address with 4 checksum bits left over. So there’s a 15/16 probability that a list of 12 words does not encode a valid address.

10x vs 10%

Posted on by John

Several years ago I asked myself a couple questions.

  1. Which things, if I were 10x better at, would make little difference?
  2. Which things, if I were 10% better at, would make a big difference?

I remember realizing, in particular, that if I knew 10x more about statistics, it wouldn’t make a bit of difference. The limiting factor on statistics projects has rarely been my knowledge of statistics. The limiting factors are things like communication, endurance, organization, etc. Getting a little better at those things has helped.

This came to mind when I ran across a couple blog posts about Emacs and org-mode. It reminded me of a time when I was convinced that mastering these tools would make me significantly more productive. That was marginally true at the time, and not true at all now.

There’s a perennial temptation to solve the problem you want to solve rather than the problem you need to solve. The former may be in the 10x category and the latter in the 10% category. I would find it more fun to explore the corners of org-mode than to deal with proposals and contracts, but the latter is what I need to do today.

There’s an adage that says it’s better to work on your strengths than your weaknesses. I generally agree with that, but with more caveats than I care to go into in this post.

Time needed to factor large integers

Posted on by John

The optimal choice of factoring algorithm depends on the size of the number you want to factor. For numbers larger than a googol (10100) the GNFS (general number field sieve) algorithm is the fastest known factoring algorithm, making GNFS the algorithm of choice for trying to factor public keys for RSA encryption

The expected time required to factor a number n using the GNFS is proportional to

exp( f(n) g(n) )

where f(n) is relatively constant and g(n) varies more strongly with n. More specifically

f(n) = (64/9)1/3 + o(1)

and

g(n) = (log n)1/3 (log log n)2/3.

The notation o(1) means a term that goes to zero as n increases. Very often in practice you can ignore o(1) terms when your value of n is large. In cryptographic applications n is certainly large, at least 21024, and yet the o(1) term is still significant for values of n seen in practice. I’ve seen one source say that for keys used in practice the o(1) term is around 0.27.

Security levels

It is widely stated that factoring a 1024-bit private key is comparable in difficulty to breaking an 80-bit symmetric encryption key, i.e. that 1024-bit keys provide 80-bit security.

To find the security level of a 1024-bit RSA key, the size of the o(1) term matters. But given this, if we want to find the security level of more RSA key sizes, it doesn’t matter how big the o(1) term is. It only that the term is roughly constant over the range of key sizes we are interested in.

If f(n) is relatively constant, then the log of the time to factor n is proportional to g(n), and the log of the time to break an encryption with security level k is proportional to k. So the security level of a key n should be proportional to g(n). Let’s see if that’s the case, using the reported security levels of various key sizes.

import numpy as np

# RSA key sizes and security levels
data = {
    1024 : 80,
    2048 : 112,
    3072 : 128,
    4096 : 140,
    7680 : 192,
}
for d in data:
    x = d*np.log(2) # natural log of 2^d
    y = x**(1/3)*(np.log(x)**(2/3)) 
    print(data[d]/y)

This prints the following:

2.5580
2.6584
2.5596
2.4819
2.6237

So the ratio is fairly constant, as expected. All the reported security levels are multiples of 4, which suggests there was some rounding done before reporting them. This would account for some of the variation above.

The output above suggests that the security level of an RSA key with b bits is roughly

2.55 x1/3 log(x)2/3

where x = log(2) b.

Aside on RSA security

RSA encryption is not broken by factoring keys but by exploiting implementation flaws.

Factoring a 2048-bit RSA key would require more energy than the world produces in a year, as explained here.

log log x

Posted on by John

This post will include some simple but useful calculations.

Throughout this post, a and b are real numbers greater than 1.

All logs are proportional

For any two bases a and b, log base a and log base b are proportional, and in fact the proportionality constant is logb a. We have

\log_b(x) = \log_b(a) \log_a(x)

or to put it another way

\frac{\log_b(x)}{\log_a(x)} = \log_b(a)

As a corollary, O( loga(x) ) = O( logb(x) ) as x → ∞. So if you say something is O(log n) and someone asks “log to what base?” the answer is “it doesn’t matter.”

Double logs are asymptotically proportional

Since loga(x) is proportional to logb(x), is loga( loga(n) ) proportional to logb( logb(n) )? No, but sorta. A little algebra shows that

\frac{\log_b( \log_b(x) )}{\log_a( \log_a(x) )} = \log_b(a) + \frac{\log_a(\log_b (a)) \log_b (a)}{ \log_a(\log_a(x))}

The second term on the right hand side goes to zero as x → ∞, and so we can write

\frac{\log_b( \log_b(x) )}{\log_a( \log_a(x) )} = \log_b(a) + o(1)

The double logs to different bases are not proportional, but they become more nearly proportional as x grows larger. As a corollary, O( loga( loga(x) ) )= O( logb( logb(x) ) ).

Note that the o(1) term goes to zero very slowly, like c / log (log x). If you’re proving a theorem in which x → ∞, you may be able to ignore this term. But for finite x, the o(1) term may be substantial, especially when a and b are far apart.

Mixed logs

I was reading a paper the other day that frequently iterated logs to different bases, which was kind of confusing. The mix could be eliminated with the following equation.

\log_a(\log_b(x)) = \log_a(b) \log_b(\log_b(x))

So mixed logs are proportional to applying the log to the inner base twice.

Checking the algebra

The algebra above is a little tedious and error-prone. Here’s some code to give complementary validation of the calculations.

from math import log
# Note that log(x, b) = log_b(x)

a, b = 3, 5

for x in [9, 29, 2025]:
    u = log(log(x, b), b) / log(log(x, a), a)
    v = log(a, b) + log(log(a, b), a)*log(a, b) / log(log(x, a), a)
    assert( abs(u - v) < 1e-15 )

    u = log(log(x, b), a)
    v = log(log(x, b), b) * log(b, a)
    assert( abs(u - v) < 1e-15 )

Related posts

Fitting a double exponential function to three points

Posted on by John

The previous post needed to fit a double exponential function to data, a function of the form

a \exp(b \exp(cx))

By taking logs, we have a function of the form

f(x) = a + b \exp(cx)

where the a in the latter equation is the log of the a in the former.

In the previous post I used a curve fitting function from SciPy to find the parameters a, b, and c. The solution in the post works, but I didn’t show all the false starts along the way. I ran into problems with overflow and with the solution method not converging before I came up with the right formulation of the problem and a good enough initial guess at the solution.

This post will look at fitting the function more analytically. I’ll still need to solve an equation numerically, but an equation in only one variable, not three.

If you need to do a regression, fitting a function with noisy data to more than three points, you could use the code below with three chosen data points to find a good starting point for a curve-fitting method.

Solution

Suppose we have x1 < x2 < x3 and we want to find a, b, and c such that

\begin{align*} y_1 &= a + b \exp(c x_1) \\ y_2 &= a + b \exp(c x_2) \\ y_3 &= a + b \exp(c x_3) \\ \end{align*}

where y1 < y2 < y3.

Subtract the equations pairwise to eliminate a:

\begin{align*} y_2 - y_1 &= b (\exp(c x_2) - \exp(c x_1)) \\ y_3 - y_1 &= b (\exp(c x_3) - \exp(c x_1)) \\ \end{align*}

Divide these to eliminate b:

\frac{y_2 - y_1}{y_3 - y_1} = \frac{\exp(c x_2) - \exp(c x_1)}{\exp(c x_3) - \exp(c x_1)}

Factor out exp(cx1) from the right side:

\frac{y_2 - y_1}{y_3 - y_1} = \frac{1 - \exp(c (x_2 - x_1))}{1 - \exp(c (x_3 - x_1))}

Now the task is to solve

L = \frac{1 - \exp(c d_2)}{1 - \exp(c d_3)}

where

\begin{align*} L &= \frac{y_2 - y_1}{y_3 - y_1} \\ d_2 &= x_2 - x_1 \\ d_3 &= x_3 - x_1 \end{align*}

Note that L, d2, and d3 are all positive.

Once we find c numerically,

b = \frac{y_2 - y_1}{\exp(c x_2) - \exp(c x_1)}

and

a = y_1 - b \exp(c x_1)

Python code

Here’s a Python implementation to illustrate and test the derivation above.

from scipy import exp
from scipy.optimize import newton

def fit(x1, x2, x3, y1, y2, y3):
    assert(x1 < x2 < x3)
    assert(y1 < y2 < y3)

    d2 = x2 - x1
    d3 = x3 - x1
    L = (y2 - y1)/(y3 - y1)
    g = lambda x: L - (1 - exp(x*d2))/(1 - exp(x*d3))
    c = newton(g, 0.315)

    b = (y2 - y1)/(exp(c*x2) - exp(c*x1))
    a = y1 - b*exp(c*x1)
    return a, b, c

a, b, c = fit(9, 25, 28, 42, 55, 92)
print([a + b*exp(c*x) for x in [9, 25, 28]])