The orbit that put men on the moon

Posted on by John

Richard Arenstorf (1929–2014) discovered a stable periodic orbit between the Earth and the Moon which was used as the basis for the Apollo missions.

His orbit is a special case of the three body problem where two bodies are orbiting in a plane, i.e. the Earth and the Moon, along with a third body of negligible mass relative to the other bodies, i.e. the satellite.

The system of differential equations for the Arenstorf orbit are

\begin{align*} x'' &= x + 2y' - \mu' \frac{x+\mu}{D_1} - \mu \frac{x - \mu'}{D_2} \\ y'' &= y - 2x' - \mu' \,\frac{y}{\,D_1} \,\,\,\,\,\,- \mu \frac{y}{\,D_2} \\ \end{align*}

where

\begin{align*} D_1 &= ((x + \mu)^2 \,+ y^2)^{3/2} \\ D_2 &= ((x - \mu')^2 + y^2)^{3/2} \end{align*}

Here the Earth is at the origin and the Moon is initially at (0, 1). The mass of the Moon is μ = 0.012277471 and the mass of the Earth is μ’ = 1-μ.

The initial conditions are

\begin{align*} x(0) &= \phantom{-}0.994 \\ x'(0) &= \phantom{-}0 \\ y(0) &= \phantom{-}0 \\ y'(0) &= -2.001585106 \end{align*}

Here’s a plot of the orbit.

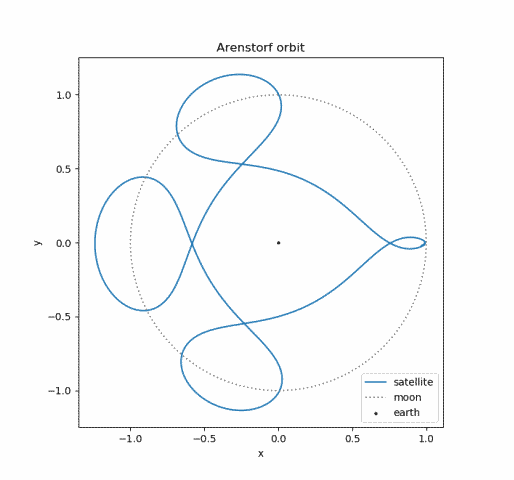
Arenstorf orbit

I found the equations above in [1] which sites the original paper [2]. Note that the paper was written in 1963, seven years before the Apollo missions. Also, before leaving NASA Arenstorf mapped out a rescue orbit. This orbit was later used on Apollo 13.

Richard Arenstorf

I was fortunate to do my postdoc at Vanderbilt before Arenstorf retired and was able to sit in on an introductory course he taught on orbital mechanics. His presentation was leisurely and remarkably clear.

His course was old-school “hard analysis,” much more concrete than the abstract “soft analysis” I had studied in graduate school. He struck me as a 19th century mathematician transported to the 20th century.

He scoffed at merely measurable functions. “Have you ever seen a function that wasn’t analytic?” This would have been heresy at my alma mater.

When I asked him about “Arenstorf’s theorem” from a recently published book I was reading, he said that he didn’t recognize it. I forget now how it was stated, maybe involving Banach spaces and/or manifolds. Arenstorf was much more concrete. He wanted to help put a man on the Moon, not see how abstractly he could state his results.

More orbital mechanics posts

[1] Hairer, Nørsett, and Wanner. Solving Ordinary Differential Equations I: Nonstiff Problems. Springer-Verlag 1987.

[2] Richard F. Arenstorf. Periodic Solutions of the Restricted Three Body Problem Representing Analytic Continuations of Keplerian Elliptic Motion. American Journal of Mathematics, Vol. 85, No. 1 (Jan., 1963), pp. 27–35.

2 thoughts on “The orbit that put men on the moon”

  1. BobC

    I’ve been looking for, and unable to find, an animation of this orbit showing the positions of all 3 bodies (well, 2 moving bodies) through time, ideally with the spacecraft velocity profile overlaid.

    I did find this Math Stack Exchange post (https://math.stackexchange.com/questions/54735/restricted-three-body-problem), but my Python-fu has ebbed a bit from its prime and I’m unsure how best to animate it and add the velocity profile.

    Anyone know of such an animation, or is willing to take a stab at it?

    A thought does come to mind: Would it be possible within KSP (Kerbal Space Program)? I haven’t used it, but this could be a fun reason to give it a try.

  2. Mr. Yacht

    Hello Dr. Cook, very pleased to read a good exposition of the topic of Arenstorf Orbit. I would like to comment about the initial position of the moon, I remember reading it (1,0) in rotating frame. In inertial frame we just ad moon orbital speed in y axis. I am working on a animation of it. I hope BobC from the previous comment can view it when I finish it.

Comments are closed.