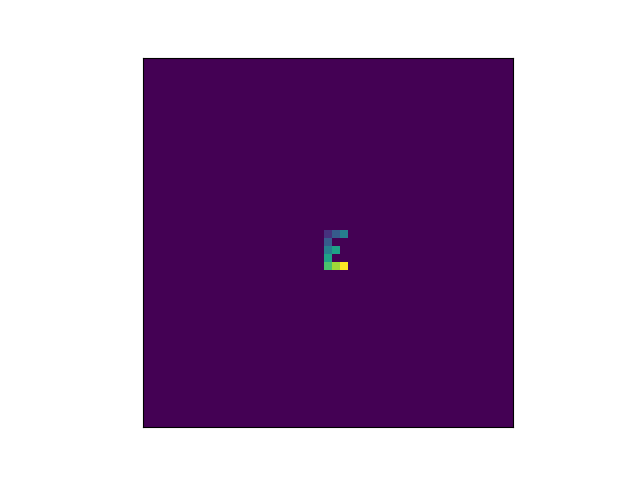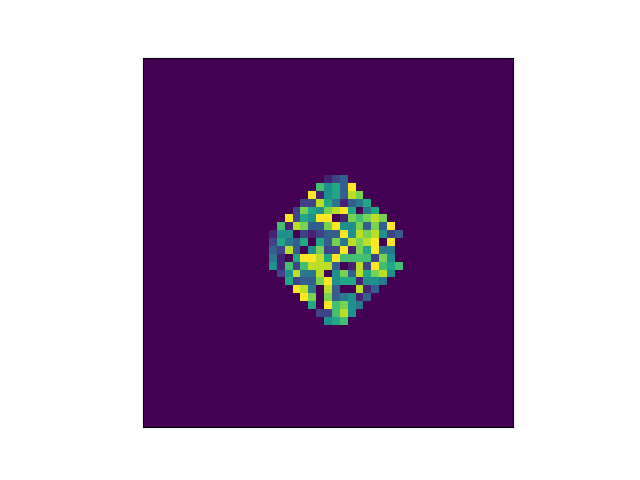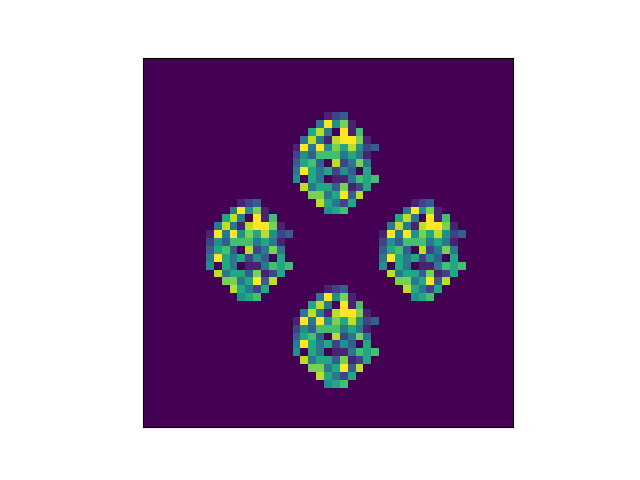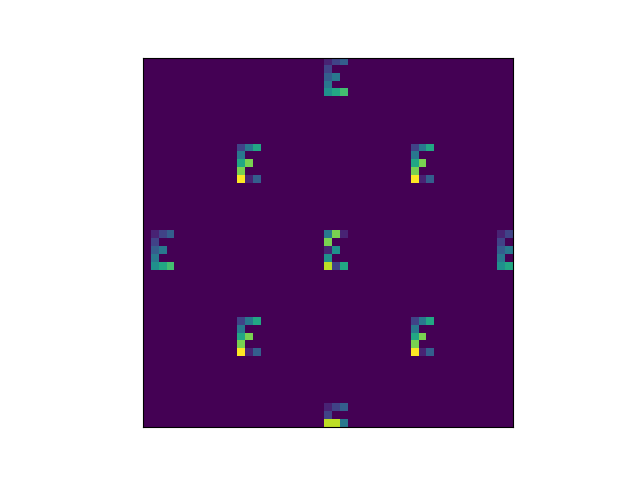The previous post looked at a cellular automaton introduced by Edward Fredkin. It has only two states: a cell is on or off. At each step, each cell is set to the sum of the states of the neighboring cells mod 2. So a cell is on if it had an odd number neighbors turned on, and is turned off if it had an even number of neighbors turned on.
You can look at cellular automata with more states, often represented as colors. If the number of states per cell is prime, then the extension of Fredkin’s automaton to multiple states also reproduces its initial pattern. Instead of taking the sum of the neighboring states mod 2, more generally you take the sum of the neighboring states mod p.
This theorem is due to Terry Winograd, cited in the same source as in the previous post.
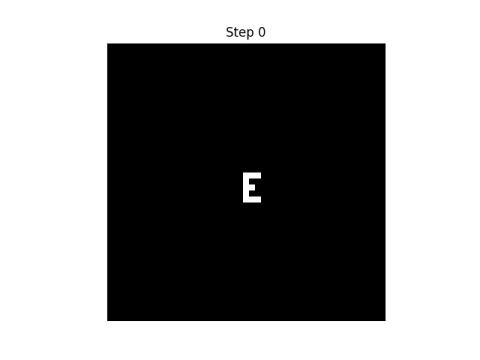
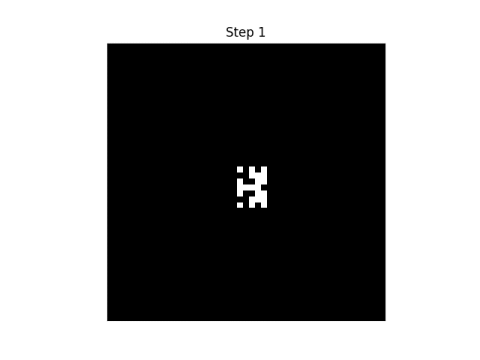
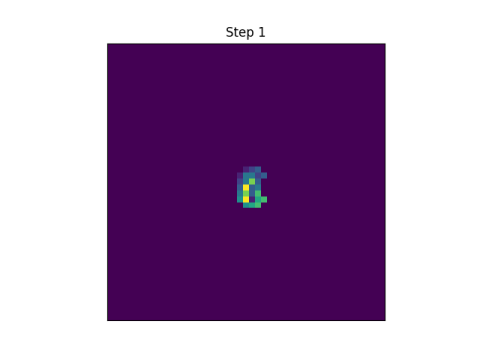
Here’s an example with 11 states. The purple background represents 0. As before, I start with an ‘E’ pattern, but I make it multi-colored.

Before turn on the automaton, we need to clarify what we mean by “neighborhood.” In this example, I mean cells to the north, south, east, and west. You could include the diagonals, but that would be different example, though still self-reproducing.
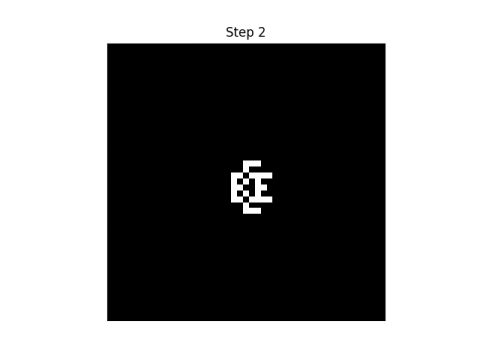
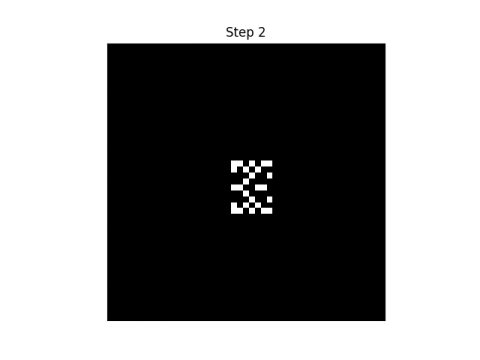
After the first step, the pattern blurs.
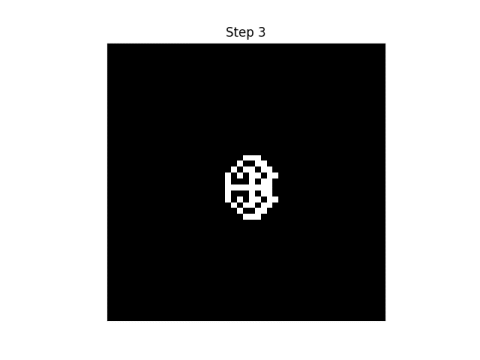
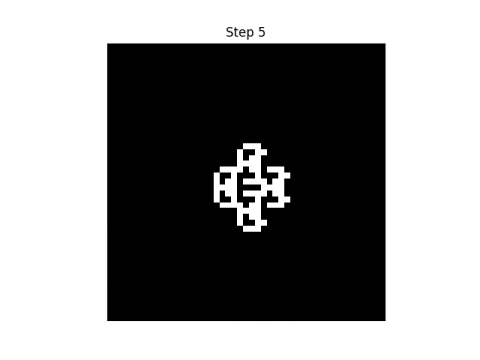
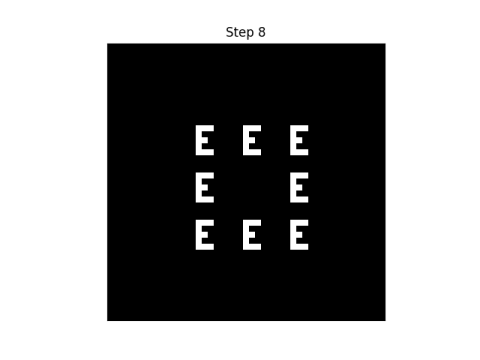
After 10 steps the original pattern is nowhere to be seen.

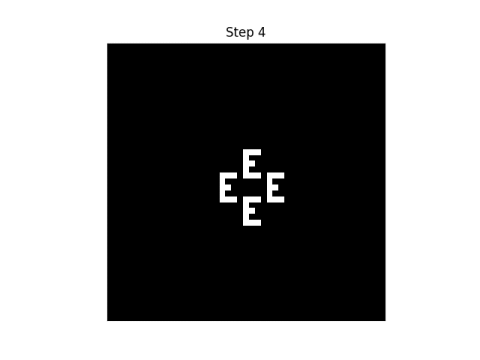
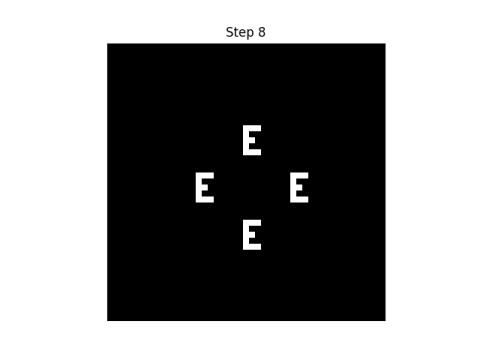
And then suddenly on the next step the pattern reappears.

I don’t know whether there are theorems on how long it takes the pattern to reappear, or how the time depends on the initial pattern, but in my experiments, the a pattern reappears after 4 steps with 2 states, 9 steps with 3 states, 5 steps with 5 states, 7 steps with 7 states, and 11 steps with 11 states.
Here’s an animation of the 11-color version, going through 22 steps.