Complex analysis

Hyperbolic metric

Posted on by John

One common model of the hyperbolic plane is the Poincaré upper half plane ℍ. This is the set of points in the complex plane with positive imaginary part. Straight lines are either vertical, a set of points with constant imaginary part, or arcs of circles centered on the real axis. The real axis is not part of ℍ. From the perspective of hyperbolic geometry these are ideal parts, infinitely far away, and not part of the plane itself.

We can define a metric on ℍ as follows. To find the distance between two points u and v, draw a line between the two points, and let a and b be the ideal points at the end of the line. By a line we mean a line as defined in the geometry of ℍ, what we would see from our Euclidean perspective as a half circle or a vertical line. Then the distance between u and v is defined as the absolute value of the log of the cross ratio (u, v; a, b).

d(u, v) = |\log (u, v; a, b) | = \left| \log \frac{|a - u|\,|b - v|}{|a - v|\,|b - u|} \right|
Cross ratios are unchanged by Möbius transformations, and so Möbius transformations are isometries.

Another common model of hyperbolic geometry is the Poincaré disk. We can use the same metric on the Poincaré disk because the Möbius transformation

z \mapsto \frac{z - i}{z + i}

maps the upper half plane to the unit disk. This is very similar to how the Smith chart is created by mapping a grid in the right half plane to the unit disk.

Update: See the next post for four analytic expressions for the metric, direct formulas involving u and v but not the ideal points a and b.

The anti-Smith chart

Posted on by John

As I’ve written about several times lately, the Smith chart is the image of a rectangular grid in the right half-plane under the function

f(z) = (z − 1)/(z + 1).

What would the image of a grid in the left half-plane look like?

For starters, since f maps the right half-plane to the interior of the unit circle, it must map the left-half plane to the exterior of the unit circle.

As we said before, the function f is a Möbius transformation, and so it takes generalized circles, i.e. either a circle or a line, to generalized circles. So the grid lines in the left half-plane are either mapped to lines or circles. Which is it?

The function f has a singularity at −1 and so the image of any line (or circle) through z = −1 is unbounded, i.e. a line, not a circle. Any line not passing through −1 has a bounded image, which must be a circle.

The line Re(z) = −1 in the z plane is mapped to the line Re(w) = 1 in the w plane. Otherwise a vertical line crossing the real axis at x is mapped to a circle passing through w = (x − 1)/(x + 1). The circle also passes through w = 1 because f(∞) = 1. The circle is symmetric about the real axis, and so this is enough information to uniquely determine the circle.

Note that (x − 1)/(x + 1) > 1 when x < −1 and so vertical lines with real part less than −1 are mapped to circles to the right of w = 1. When −1 < x < 0, vertical lines are mapped to circles to the left of w = 1.

The images of horizontal lines we’ve looked at before. These are all circles passing through w = 1 and tangent to the circles that are images of vertical lines. But this time instead of taking the portion of the circles inside the unit circle, we take the portion outside the unit circle.

And without further ado, we present the anti-Smith chart, the image of a grid in the left half plane.

 

Cross ratio

Posted on by John

The cross ratio of four points A, B, C, D is defined by

(A, B; C, D) = \frac{AC \cdot BD}{BC \cdot AD}

where XY denotes the length of the line segment from X to Y.

The idea of a cross ratio goes back at least as far as Pappus of Alexandria (c. 290 – c. 350 AD). Numerous theorems from geometry are stated in terms of the cross ratio. For example, the cross ratio of four points is unchanged under a projective transformation.

Complex numbers

The cross ratio of four (extended [1]) complex numbers is defined by

(z_1, z_2; z_3, z_4) = \frac{(z_3 - z_1)(z_4 - z_2)}{(z_3 - z_2)(z_4 - z_1)}

The absolute value of the complex cross ratio is the cross ratio of the four numbers as points in a plane.

The cross ratio is invariant under Möbius transformations, i.e. if T is any Möbius transformation, then

(T(z_1), T(z_2); T(z_3), T(z_4)) = (z_1, z_2; z_3, z_4)

This is connected to the invariance of the cross ratio in geometry: Möbius transformations are projective transformations on a complex projective line. (More on that here.)

If we fix the first three arguments but leave the last argument variable, then

T(z) = (z_1, z_2; z_3, z) = \frac{(z_3 - z_1)(z - z_2)}{(z_3 - z_2)(z - z_1)}

is the unique Möbius transformation mapping z1, z2, and z3 to ∞, 0, and 1 respectively.

The anharmonic group

Suppose (a, b; c, d) = λ ≠ 1. Then there are 4! = 24 permutations of the arguments and 6 corresponding cross ratios:

\lambda, \frac{1}{\lambda}, 1 - \lambda, \frac{1}{1 - \lambda}, \frac{\lambda - 1}{\lambda}, \frac{\lambda}{\lambda - 1}

Viewed as functions of λ, these six functions form a group, generated by

\begin{align*} f(\lambda) &= \frac{1}{\lambda} \\ g(\lambda) &= 1 - \lambda \end{align*}

This group is called the anharmonic group. Four numbers are said to be in harmonic relation if their cross ratio is 1, so the requirement that λ ≠ 1 says that the four numbers are anharmonic.

The six elements of the group can be written as

\begin{align*} f(\lambda) &= \frac{1}{\lambda} \\ g(\lambda) &= 1 - \lambda \\ f(f(\lambda)) &= g(g(\lambda) = z \\ f(g(\lambda)) &= \frac{1}{\lambda - 1} \\ g(f(\lambda)) &= \frac{\lambda - 1}{\lambda} \\ f(g(f(\lambda))) &= g(f(g(\lambda))) = \frac{\lambda}{\lambda - 1} \end{align*}

Hypergeometric transformations

When I was looking at the six possible cross ratios for permutations of the arguments, I thought about where I’d seen them before: the linear transformation formulas for hypergeometric functions. These are, for example, equations 15.3.3 through 15.3.9 in A&S. They relate the hypergeometric function F(a, b; c; z) to similar functions where the argument z is replaced with one of the elements of the anharmonic group.

I’ve written about these transformations before here. For example,

F(a, b; c; z) = (1-z)^{-a} F\left(a, c-b; c; \frac{z}{z-1} \right)

There are deep relationships between hypergeometric functions and projective geometry, so I assume there’s an elegant explanation for the similarity between the transformation formulas and the anharmonic group, though I can’t say right now what it is.

Related posts

[1] For completeness we need to include a point at infinity. If one of the z equals ∞ then the terms involving ∞ are dropped from the definition of the cross ratio.

How to make a Smith chart

Posted on by John

The Smith chart from electrical engineering is the image of a Cartesian grid under the function

f(z) = (z − 1)/(z + 1).

More specifically, it’s the image of a grid in the right half-plane.

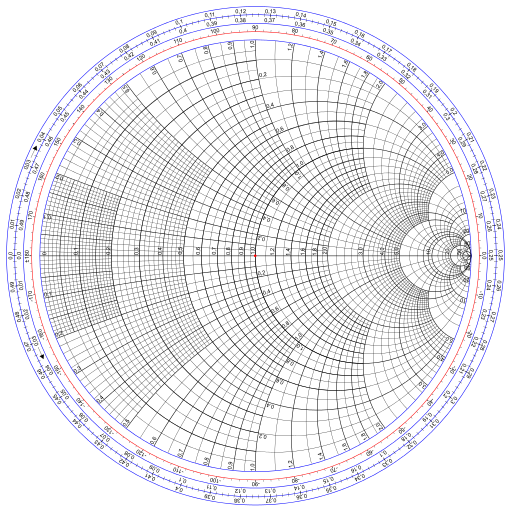
Smith chart

This post will derive the basic mathematical properties of this graph but will not go into the applications. Said another way, I’ll explain how to make a Smith chart, not how to use one.

We will use z to denote points in the right half-plane and w to denote the image of these points under f. We will speak of lines in the z plane and the circles they correspond to in the w plane.

Möbius transformations

Our function f is a special case of a Möbius transformation. There is a theorem that says Möbius transformation map generalized circles to generalized circles. Here a generalized circle means a circle or a line; you can think of a line as a circle with infinite radius. We’re going to get a lot of mileage out of that theorem.

Image of the imaginary axis

The function f maps the imaginary axis in the z plane to the unit circle in the w plane. We can prove this using the theorem above. The imaginary axis is a line, so it’s image is either a line or a circle. We can take three points on the imaginary axis in the z plane and see where they go.

When we pick z equal to 0, i, and −i from the imaginary axis we get w values of −1, i, and −i. These three w values do not line on a line, so the image of the imaginary axis must be a circle. Furthermore, three points uniquely determine a circle, so the image of the imaginary axis is the circle containing −1, i, and −i, i.e. the unit circle.

Image of the right half-plane

The imaginary axis is the boundary of the right half-plane. Since it is mapped to the unit circle, the right half-plane is either mapped to the interior of the unit circle or the exterior of the unit circle. The point z = 1 goes to w = 0, and so the right half-plane is mapped inside the unit circle.

Images of vertical lines

Let’s think about what happens to vertical lines in the z plane, lines with constant positive real part. The images of these lines in the w plane must be either lines or circles. And since the right-half plane gets mapped inside the unit circle, these lines must get mapped to circles.

We can say a little more. All lines contain the point ∞, and f(∞) = 1, so the image of every vertical line in the z plane is a circle in the w plane, inside the unit circle and tangent to the unit circle at w = 1. (Tossing around ∞ is a bit informal, but it’s easy to make rigorous.)

The vertical lines in the z plane

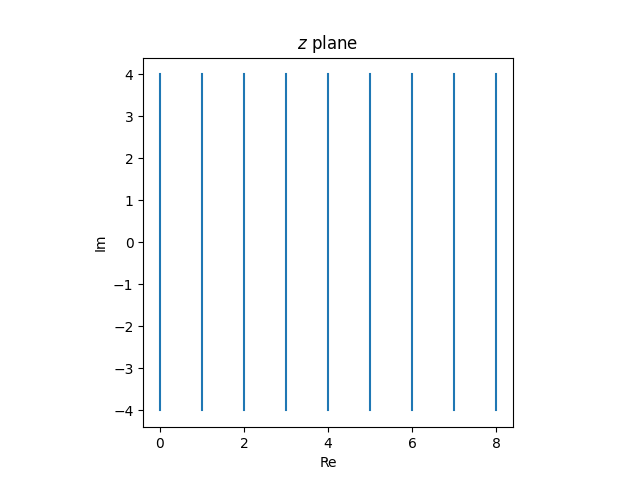
map to tangent circles in the w plane.

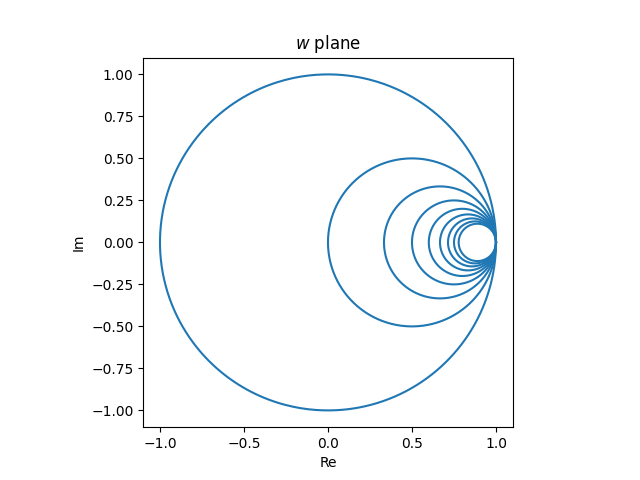
Images of horizontal lines

Next, let’s think about horizontal lines in the z plane, lines with constant imaginary part. The image of these lines is either a line or a circle. Which is it? The image of a line is a line if it contains ∞, otherwise it’s a circle. Now f(z) = ∞ if and only if z = −1, and so the image of the real axis is a line, but the image of every other horizontal line is a circle.

Since f(∞) = 1, the image of every horizontal line passes through 1, just as the images of all the vertical lines passes through 1.

Since horizontal lines extend past the right half-plane, the image circles extend past the unit circle. The part of the line with positive real part gets mapped inside the unit circle, and the part of the line with negative real part gets mapped outside the unit circle. In particular, the image of the positive real axis is the interval [−1, 1].

Möbius transformations are conformal maps, and so they preserve angles of intersection. Since horizontal lines are perpendicular to vertical lines, the circles that are the images of the horizontal lines meet the circles that are the images of vertical lines at right angles.

The horizontal rays in the z plane

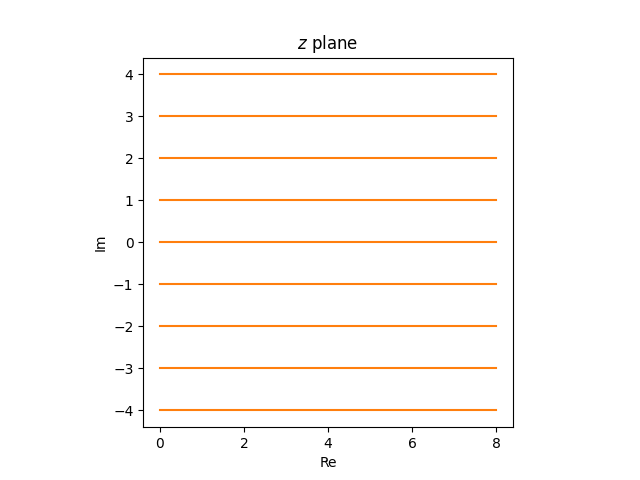
become partial circles in the w plane.

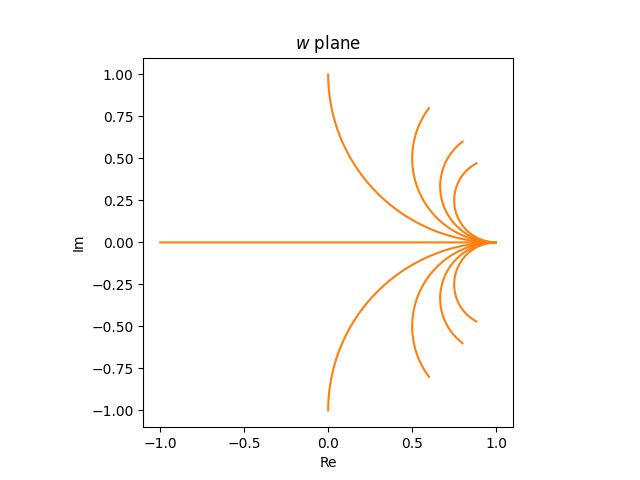
If we were to look at horizontal lines rather than rays, i.e. if we extended the lines into the left half-plane, the images in the w plane would be full circles.

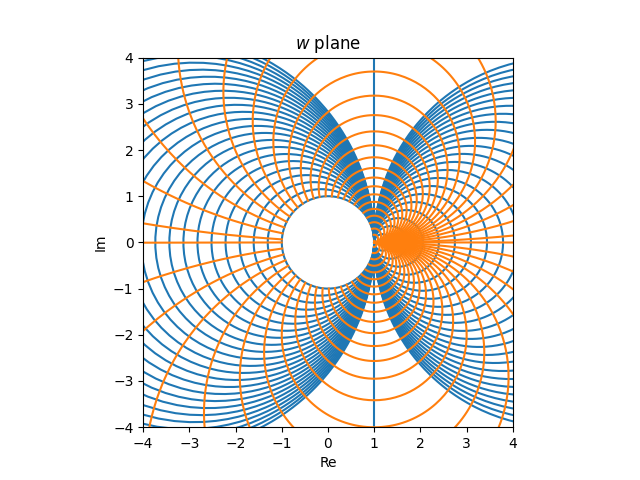
Now let’s put our images together. The grid

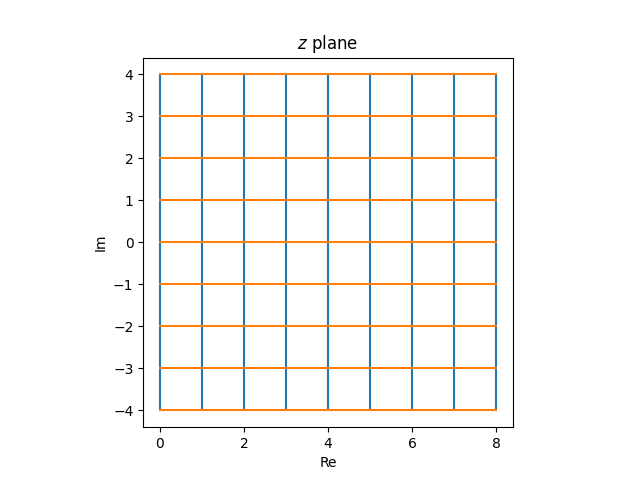
in the z plane becomes the following in the w plane.

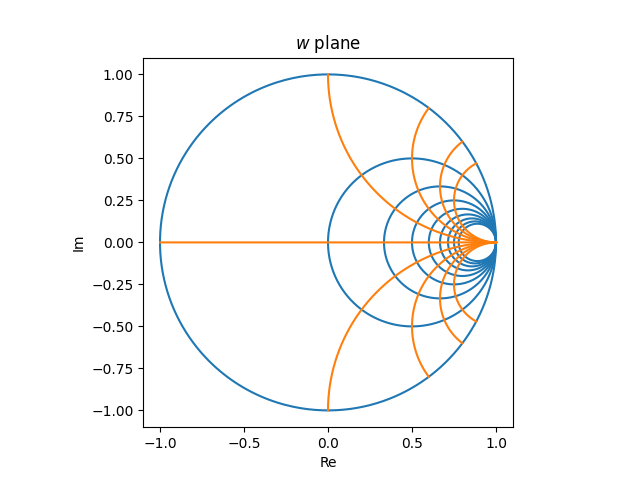
Spacing

An evenly spaced grid in the z plane becomes a very unevenly spaced graph in the w plane. Things are crowded on the right hand side and sparse on the left. A usable Smith chart needs to be roughly evenly filled in, which means it has to be the image of an unevenly filled in grid in the z plane. For example, you’d need more vertical lines in the z plane with small real values than with large real values.

I address the issue of spacing in the next post.

Inverting matrices and bilinear functions

Posted on by John

The inverse of the matrix

M = \begin{bmatrix} a & b \\ c & d \end{bmatrix}

is the matrix

M^{-1} = \frac{1}{|M|} \begin{bmatrix} d & -b \\ -c & a \end{bmatrix} = \frac{1}{ad - bc} \begin{bmatrix} d & -b \\ -c & a \end{bmatrix}

assuming ad − bc ≠ 0.

Also, the inverse of the bilinear function (a.k.a. Möbius transformation)

f(z) = \frac{az + b}{cz + d}

is the function

f^{-1}(z) = \frac{dz - b}{-cz + a}

again assuming ad − bc ≠ 0.

The elementary takeaway is that here are two useful equations that are similar in appearance, so memorizing one makes it easy to memorize the other. We could stop there, but let’s dig a little deeper.

There is apparently an association between 2 × 2 matrices and Möbius transformations

\frac{az + b}{cz + d} \leftrightarrow \begin{bmatrix} a & b \\ c & d \end{bmatrix}

This association is so strong that we can use it to compute the inverse of a Möbius transformation by going to the associated matrix, inverting it, and going back to a Möbius transformation. In diagram form, we have the following

Now there are a few loose ends. First of all, we don’t really have a map between Möbius transformations and matrices per se; we have a map between a particular representation of a Möbius transformation and a 2 × 2 matrix. If we multiplied a, b, c, and d in a Möbius transformation by 10, for example, we’d still have the same transformation, just a different representation, but it would go to a different matrix.

What we really have is a map between Möbius transformations and equivalence classes of invertible matrices, where two matrices are equivalent if one is a non-zero multiple of the other. If we wanted to make the diagram above more rigorous, we’d replace ℂ2×2 with PL(2, ℂ), linear transformations on the complex projective plane. In sophisticated terms, our map between Möbius transformations and matrices is an isomorphism between automorphisms of the Riemann sphere and PL(2, ℂ).

Möbius transformations act a lot like linear transformations because they are linear transformations, but on the complex projective plane, not on the complex numbers. More on that here.

Area of the unit disk after a Möbius transformation

Posted on by John

Let f(z) = (az + b)/(cz + d) where Δ = ad − bc ≠ 1.

If f has no singularity inside the unit disk, i.e. if |d/c| > 1, then the image of the unit disk under f is another disk. What is the area of that disk?

The calculation is complicated, but the result turns out to be

Area = π |Δ|² / (|d|² − |c|²)².

Just as a sanity check, set c = 0 and d = 1. Then we multiply the disk by a and shift by b. The shift doesn’t change the area, and multiplying by a multiples the area by |a|², which is consistent with our result.

As another sanity check, note that the area is infinite if c = d, which is correct since there would be a singularity at z = −1.

Finally, here’s a third sanity check in the form of Python code.

from numpy import linspace, pi, exp

a, b, c, d = 9, 15j, 20, 25j
theory_r = abs(a*d - b*c)/(abs(d)**2 - abs(c)**2)
print("theory r:", theory_r)

t = linspace(0, 2*pi, 10000)
z = exp(1j*t)
w = (a*z + b)/(c*z + d)
approx_r = (max(w.real) - min(w.real))/2
print("approx r:", approx_r)

Area of unit disk under a univalent function

Posted on by John

Let D be the unit disk in the complex plane and let f be a univalent function on D, meaning it is analytic and one-to-one on D.

There is a simple way to compute the area of f(D) from the coefficients in its power series.

If

f(z) = \sum_{n=0}^\infty c_n z^n

then

\text{area}\left(f(D)\right) = \int_D |f^\prime(z)|^2 \, dx \,dy = \pi \sum_{n=1}^\infty n |c_n|^2

The first equality follows from the change of variables theorem for functions of two variables and applying the Cauchy-Riemann equations to simplify the Jacobian. The second equality is a straight-forward calculation that you can work out in polar coordinates.

Application

Let’s apply this to what I called the minimalist Mandelbrot set the other day.

The orange disk has radius 1/4 and so its area is simply π/16.

Finding the area of the blue cardioid takes more work, but the theorem above makes it easy. The cardioid is the image of the set {α : |α| < ½} under the map f(z) = z − z². To apply the theorem above we need the domain to be the unit disk, not the unit disk times ½, so we define

f(z) = \frac{1}{2} z - \frac{1}{4} z^2

as a function on the unit disk. Now c1 = ½ and c2 = −¼ and so the area of f(D) = 3π/8.

I said in the earlier post that the minimalist Mandelbrot set makes up most of the Mandelbrot set. Now we can quantify that. The area of the minimalist Mandelbrot set is 7π/16 = 1.3744. The area of the Mandelbrot set is 1.5065, so the minimalist set shown above makes up over 91% of the total area.

Related posts

Minimalist Mandelbrot set

Posted on by John

The Mandelbrot set is one of the most famous fractals. It consists of the complex numbers c such that iterations of

f(z) = z² + c

are bounded. The plot of the Mandelbrot set is a complicated image—it’s a fractal, after all—and yet there’s a simple description of an first approximation to the Mandelbrot set.

As shown in [1], the image of the disk

{α : |α| < ½}

under the map taking z to z − z² gives the set of all points where iterations of f converge to a point. This is the blue cardioid region. Call it A.

Also show in [1] is that the points

B = {c : |1 + c| < ¼}

are the ones such that f(f(z)) converges to a fixed point.

These two parts form the core of the Mandelbrot set. The blue heart-shaped region on the right is A and the orange disk on the left is B.

The rest of the Mandelbrot set are the points where iterations of f remain bounded but have more complicated behavior than the points in A or B.

[1] Alan F. Beardon. Iteration of Rational Functions. Springer-Verlag, 1991.

The biggest math symbol

Posted on by John

The biggest math symbol that I can think of is the Riemann P-symbol

w(z)=P \left\{ \begin{matrix} a & b & c & \; \\ \alpha & \beta & \gamma & z \\ \alpha^\prime & \beta^\prime & \gamma^\prime & \; \end{matrix} \right\}

The symbol is also known as the Papperitz symbol because Erwin Papperitz invented the symbol for expressing solutions to Bernard Riemann’s differential equation.

Before writing out Riemann’s differential equation, we note that the equation has regular singular points at a, b, and c. In fact, that is its defining feature: it is the most general linear second order differential equation with three regular singular points. The parameters a, b, and c enter the equation in the as roots of an expression in denominators; that’s as it has to be if these are the singular points.

The way the Greek letter parameters enter Riemann’s equation is more complicated, but there is a good reason for the complication: the notation makes solutions transform as simply as possible under a bilinear transformation. This is important because Möbius transformations are the conformal automorphisms of the Riemann sphere.

To be specific, let

m(z) = \frac{Az + B}{Cz + D}

be a Möbius transformation. Then

P \left\{ \begin{matrix} a & b & c & \; \\ \alpha & \beta & \gamma & z \\ \alpha^\prime & \beta^\prime & \gamma^\prime & \; \end{matrix} \right\} = P \left\{ \begin{matrix} m(a) & m(b) & m(c) & \; \\ \alpha & \beta & \gamma & m(z) \\ \alpha^\prime & \beta^\prime & \gamma^\prime & \; \end{matrix} \right\}

Since the parameters on the top row of the P-symbol are the locations of singularities, when you transform a solution, moving the singularities, the new parameters have to be the new locations of the singularities. And importantly the rest of the parameters do not change.

Now with the motivation aside, we’ll write out Riemann’s differential equation in all its glory.

\frac{d^2w}{dz^2} + p(z) \frac{dw}{dz} + q(z) \frac{w}{(z-a)(z-b)(z-c)} = 0

where

p(z) = \frac{1-\alpha-\alpha^\prime}{z-a} + \frac{1-\beta-\beta^\prime}{z-b} + \frac{1-\gamma-\gamma^\prime}{z-c}

and

q(z) = \frac{\alpha\alpha^\prime (a-b)(a-c)} {z-a} +\frac{\beta\beta^\prime (b-c)(b-a)} {z-b} +\frac{\gamma\gamma^\prime (c-a)(c-b)} {z-c}

Related posts

Knuth’s Twindragon

Posted on by John

A few days ago I wrote about a random process that creates a fractal known as the Twin Dragon. This post gives a deterministic approach to create the same figure.

As far as I can tell, the first reference to this fractal is in a paper by Davis and Knuth in the Journal of Recreational Mathematics from 1970. Unfortunately this journal is out of print and hard or impossible to find online [1]. Knuth presents the twindragon (one word, lowercase) fractal in TAOCP Vol 2, page 206.

Knuth defines the twindragon via numbers base b = 1 − i. Every complex number can be written in the form

z = \sum_{k=-\infty}^\infty a_k (1 - i)^k

where the “digits” ak are either 0 or 1.

The twindragon fractal is the set of numbers that only have non-zero digits to the right of the decimal point, i.e. numbers of the form

z = \sum_{k=1}^\infty a_k (1 - i)^{-k}

I implemented this in Python as follows.

import matplotlib.pyplot as plt
from itertools import product

for bits in product([0, 1], repeat=15):
    z = sum(a*(1-1j)**(-k) for k, a in enumerate(bits))
    plt.plot(z.real, z.imag, 'bo', markersize=1)
plt.show()

This produced the image below.

Related posts

[1] If you can find an archive of Journal of Recreational Mathematics, please let me know.