I was looking today at a cardboard box that had the “this way up” symbol on it and wondered whether there is a Unicode value for it.

Apparently not. But there is an ISO code for it: ISO 7000 symbol 0623. It’s an international standard symbol for indicating how to orient a package. The name says it all: this way up.

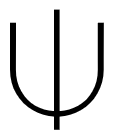
There is a similar symbol in math and computer science: ↑↑. This is so-called up-arrow notation, introduced by Donald Knuth in 1976 [1].

In Knuth’s notation, ↑ indicates exponentiation, i.e. repeated multiplication, and ↑↑ indicates repeated exponentiation. There’s a little ambiguity here: we have to clarify in what order we apply exponentiation. Knuth stipulated that ↑↑ is right-associative, i.e.

So, for example, 5 ↑↑ 3 equals 5¹²⁵, not 125⁵.

In general, n arrows means to repeatedly apply n − 1 arrows. If we use ↑ⁿ as a shortcut for writing n up arrows, then we can define ↑ⁿ recursively as meaning we apply ↑ⁿ⁻¹ n times.

What I find most interesting about Knuth’s notation is how rarely it is used. I don’t think it’s because anyone object’s to Knuth’s notation; it’s just that there isn’t much need for what the notation represents. It’s primary use may be theoretical computer science. There you sometimes want to construct functions that grow ridiculously fast, such as Ackermann’s function, and functions of the form a ↑ⁿ b are good for that.

This is curious. Multiplication is repeated addition, exponentiation is repeated multiplication, and so repeated exponentiation seems like a natural extension. I won’t say that it’s unnatural, but it is very uncommon.

Related posts

• Engine coolant temperature symbol
• Conditional independence notation
• i^i^i …

[1] Donald E. Knuth. “Mathematics and Computer Science: Coping with Finiteness”. Science. 194 (4271): 1235–1242.

The factorial of an integer n is the product of the positive integers up to n.

The double factorial of an even (odd) integer n is the product of the positive even (odd) integers up to n. For example,

8!! = 8 × 6 × 4 × 2

and

9!! = 9 × 7 × 5 × 3 × 1.

Double factorials come up fairly often, and sometimes triple, quadruple, or higher multifactorials do too.

In general, the k-factorial of n is the product of the positive integers up to n that are congruent to n mod k. Here’s how you might implement k-factorials in Python.

    from operator import mul
    from functools import reduce

    def multifactorial(n, k):
        return reduce(mul, [i for i in range(1, n+1) if (n-i)%k == 0], 1)

Update: As pointed out in the comments, multifactorial could be implemented more succinctly as

    def multifactorial(n, k):
        return reduce(mul, range(n, 0, -k), 1)

Factorial notation is a little awkward, and multifactorial notation is even more awkward. Someone seeing n!! for the first time might reasonably assume it means (n!)!, but it does not.

Adding exclamation points works, albeit awkwardly, for specific values of k, but not for variable numbers of k. One way I’ve seen to express k-factorials for variable k is to add a subscript (k) to the factorial:

I’ve also seen the subscript on the exclamation point written as a superscript instead.

I’d like to suggest a different notation: Π_k. by analogy with the Π function.

When k ≡ 1 the condition i ≡ n (mod k) always holds, and we have factorial, i.e.

Π₁(n) = Π(n) = n!.

One downside of this notation is that while the function Π is defined for all complex numbers (aside from singularities at negative integers) the function Π_k is only defined for positive integer arguments. Still, in my opinion, this is less awkward than the alternatives I’ve seen.

By the way, the term “double factorial” seems backward. Maybe it should have been “half factorial” because you’re multiplying half as many numbers together, not twice as many. “Multifactorial” in general seems like an unfortunate name. Subfactorial might have been better, but unfortunately that name means something else.

I understand why someone may have come up with the idea of using two exclamation points for what we call double factorial; it would be hard to draw half an exclamation point. An advantage of the notation suggested here is that it suggests that there’s a variation on factorial somehow associated with k, but there’s no implication of multiplying or dividing by k.

Adding “mod k” as a subscript would be even more explicit than a subscript k. Someone who hadn’t seen

Π_{mod k} (n)

before might be able to figure out what it means; I think they would at least easily remember what it means once told. And the presence of “mod” might suggest to the reader that the argument needs to be an integer.

Mathematics notation changes slowly over time, generally for the better. I can’t think of an instance that I think was a step backward.

Gauss introduced the notation [x] for the greatest integer less than or equal to x in 1808. The notation was standard until relatively recently, though some authors used the same notation to mean the integer part of x. The two definitions agree if x is positive, but not if x is negative.

Not only is there an ambiguity between the two meanings of [x], it’s not immediately obvious that there is an ambiguity since we naturally think first of positive numbers. This leads to latent errors, such as software that works fine until the first person gives something a negative input.

In 1962 Kenneth Iverson introduced the notation ⌊x⌋ (“floor of x“) and ⌈x⌉ (“ceiling of x“) in his book A Programming Language, the book that introduced APL. According to Concrete Mathematics, Iverson

found that typesetters could handle the symbols by shaving off the tops and bottoms of ‘[‘ and ‘]’.

This slight modification of the existing notation made things much clearer. The notation [x] is not mnemonic, but clearly ⌊x⌋ means to move down and ⌈x⌉ means to move up.

Before Iverson introduced his ceiling function, there wasn’t a standard notation for the smallest integer greater than or equal to x. If you did need to refer to what we now call the ceiling function, it was awkward to do so. And if there was a symmetry in some operation between rounding down and rounding up, the symmetry was obscured by asymmetric notation.

My impression is that ⌊x⌋ became more common than [x] somewhere around 1990, maybe earlier in computer science and later in mathematics.

Iverson and APL

Iverson’s introduction of the floor and ceiling functions was brilliant. The notation is mnemonic, and it filled what in retrospect was a gaping hole. In hindsight, it’s obvious that if you have a notation for what we now call floor, you should also have a notation for what we now call ceiling.

Iverson also introduced the indicator function notation, putting a Boolean expression in brackets to denote the function that is 1 when the expression is true and 0 when the expression is false. Like his floor and ceiling notation, the indicator function notation is brilliant. I give an example of this notation in action here.

I had a small consulting project once where my main contribution was to introduce indicator function notation. That simple change in notation made it clear how to untangle a complicated calculation.

Since two of Iverson’s notations were so simple and useful, might there be more? He introduced a lot of new notations in his programming language APL, and so it makes sense to mine APL for more notations that might be useful. But at least in my experience, that hasn’t paid off.

I’ve tried to read Iverson’s lecture Notation as a Tool of Thought several times, and every time I’ve given up in frustration. Judging by which notations have been widely adopted, the consensus seems to be that the floor, ceiling, and indicator function notations were the only ones worth stealing from APL.

This evening I ran across a dialog that suggests that decimal notation is wrong.

It happened when I started learning about decimals in school. I knew then that ten has one zero, a hundred has two, a thousand three, and so on. And then this teacher starts saying that tenth doesn’t have any zero, a hundredth has only one, a thousandth has only two, and so on. … Only much later did I have enough perspective to put my finger on the problem: The decimal point is always misplaced!

Source: Conics. Emphasis in the original.

The proposed solution is to put the decimal point above the units position rather than after it. Then the notation would be symmetric. For example, 1000 and 1/1000 would look like this:

Of course decimal notation isn’t likely to change, but the author makes an interesting point.

Here are some of my favorite notations that are not commonly used.

The first is Richard Stanley’s notation for counting the number of ways to select k objects from a set of n objects with replacement. This is similar to the problem solved by binomial coefficients, but not the same since binomial coefficients count the number of possible selections without replacement. Stanley’s symbol is

I like this symbol for two reasons. First, it’s good to have a notation, any notation, for a concept that comes up fairly often. Second, it’s appropriate for this symbol to resemble the binary coefficient symbol. See selecting with replacement for more on Stanley’s symbol, how to think about it and how to compute it.

Next is Kenneth Iverson’s notation for indicator functions. Iverson’s idea was to put a Boolean condition in square brackets to indicate the function that is 1 when that condition is true and 0 otherwise. For example, [x > y] is the function f(x, y) such that f equals 1 when x is greater than y and equals 0 for all other arguments. This notation saves ink and makes it easier to concentrate on the substance of an expression. For more on Iverson’s notation, see Concrete Mathematics.

Another notation from Concrete Mathematics is the use of a perpendicular symbol to note that two integers are relatively prime. For example, m ⊥ n would indicate that that m and n are relatively prime. The more common way to denote this would be to say gcd(m, n) = 1. The perpendicular symbol is nice because perpendicular lines have no component of direction in common, just as relative prime numbers have no prime factors in common.

Finally, multi-index notation is a handy way to make multivariable theorems easier to remember. For example, with this notation, Taylor series in several variables look similar to Taylor series in one variable.

Related link: Stanley’s twelvefold way