Physics

Manga guides to physics and the universe

Posted on by John

I recently received review copies of the Manga Guides to physics and the universe. These made a better impression than the relativity guide that I reviewed earlier. The guide to physics has been out for a while. The guide to the universe comes out June 24.

The Manga Guide to Physics basically covers force, momentum, and energy. The pace is leisurely. There’s not much back story; it cuts to the chase fairly quickly.This guide will not prepare you to solve physics problems, but it does give you a good overview of the basics.

(These books are not entirely manga; all three books I’ve seen in the series have several pages of more traditional textbook content.)

The Manga Guide to the Universe gives a tour of cosmology from the geocentric view to current theories. It contains some very recent material, such as references to the WMAP project.

This book is more rushed than the physics guide. That’s to be expected considering its ambitious scope. It devotes a fairly large amount of space to the back story and this contributes to the book being rushed.

I mentioned in my review of The Manga Guide to Relativity that although Americans associate cartoons with children, that book was not written for children. The physics guide, however, would be appropriate for a wide range of readers. Young readers may not fully appreciate the content, but they would not find anything offensive.

The Manga Guide to the Universe is inoffensive with one exception. There are a couple provocative frames in the prologue that will keep the book off some school library shelves.

What was the most important event of the 19th century?

Posted on by John

According to Richard Feynman, the most important event of the 19th century was the discovery of the laws of electricity and magnetism.

From a long view of the history of mankind—seen from, say, ten thousand years from now—there can be little doubt that the most significant event of the 19th century will be judged as Maxwell’s discovery of the laws of electrodynamics. The American Civil War will pale into provincial insignificance in comparison with this important scientific event of the same decade.

From The Feynman Lectures on Physics, Volume 2.

Related post: Grand unified theory of 19th century math

Manga Guide to Relativity

Posted on by John

A few days ago I got a review copy of The Manga Guide to Relativity (ISBN 1593272723). This is an English translation of a book first published in Japanese a couple years ago.

I assume the intended audience, at least for the original Japanese edition, is familiar with manga and wants to learn about relativity. I came from the opposite perspective, more familiar with relativity than manga, so I paid more attention to the background than the foreground. My experience was more like reading The Relativity Guide to Manga.

I expected The Manga Guide to Relativity to be something like The Cartoon Guide to Genetics. However, the former has much less scientific content than the latter. A fair amount of the relativity book is background story, and the substantial parts are repetitive. As I recall, the genetics book was much more dense with information, though presented humorously.

Some parents and teachers will buy The Manga Guide to Relativity to introduce children to science in an entertaining genre. These folks may be surprised to discover the sexual undertones in the book. Americans typically equate comics with children, but the book was originally written for a Japanese audience that does not have the same view.

Final velocity

Posted on by John

My daughter and I were going over science homework this evening. A ball falls for 10 seconds. What is its final velocity?

JC: So how fast is the ball going when it hits the ground?

RC: Zero. It stops before it bounces back up.

JC: Well, how fast is it going just before it hits the ground?

RC: They didn’t ask the almost final velocity. They asked for the final velocity.

Coming full circle

Posted on by John

Experts often end up where they started as beginners.

If you’ve never seen the word valet, you might pronounce it like VAL-it. If you realize the word has a French origin, you would pronounce it val-A. But the preferred pronunciation is actually VAL-it.

Beginning musicians play by ear, to the extent that they can play at all. Then they learn to read music. Eventually, maybe years later, they realize that music really is about what you hear and not what you see.

Beginning computer science students think that computer science is all about programming. Then they learn that computer science is actually about computation in the abstract and not about something so vulgar as a computer. But eventually they come back down to earth and realize that 99.44% of computer science is ultimately motivated by the desire to get computers to do things.

In a beginning physics class, an instructor will ask students to assume a pulley has no mass and most students will simply comply. A few brighter students may snicker, knowing that pulleys really do have mass and that some day they’ll be able to handle problems with realistic pulleys. In a more advanced class, it’s the weaker students who snicker at massless pulleys. The better students understand a reference to a massless pulley to mean that in the current problem, the rotational inertia of the pulley can safely be ignored, simplifying the calculations without significantly changing the result. Similar remarks hold for frictionless planes and infinite capacitors as idealizations. Novices accept them uncritically, sophomores sneer at them, and experts understand their uses and limitations. (Two more physics examples.)

Here’s an example from math. Freshmen can look at a Dirac function δ(x) without blinking. They accept the explanation that it’s infinite at the origin, zero everywhere else, and integrates to 1. Then when they become more sophisticated, they realize this explanation is nonsense. But if they keep going, they’ll learn the theory that makes sense of things like δ(x). They’ll realize that the freshman explanation, while incomplete, is sometimes a reasonable intuitive guide to how δ(x) behaves. They’ll also know when such intuition leads you astray.

In each of these examples, the experts don’t exactly return to the beginning. They come to appreciate their initial ideas in a more nuanced way.

“When we travel, we travel not to see new places with new eyes; but that when we come home we see home with new eyes.” — G. K. Chesterton

Related posts

A childhood question about heat

Posted on by John

When I was a little kid, I asked some adults the following question.

If hot things cool, and cool things warm up, could something hot cool down and warm back up?

The people I asked didn’t understand my question and just laughed. I have no idea how old I was, but I wasn’t old enough to articulate what I was thinking.

Here’s what I had in mind. I knew that hot things like a cup of coffee grew cold. And I knew that cold things, say a glass of milk, get warm. Well, could the coffee get so cold that it becomes a cold thing and start to warm back up?

Could the coffee become as cold as the glass of milk? Common sense suggests that can’t happen. When we say coffee grows cold, we mean that it becomes relatively colder, closer to room temperature. And when we say the milk is getting warm, we also mean it is getting closer to room temperature. We’ve never left a hot cup of coffee on a table and come back later to find that it has cooled off so much that it is colder than room temperature. But could there be small fluctuations?

As the coffee and milk head toward room temperature, could they overshoot the target, just by a little bit? Say room temperature is 70 °F, the coffee starts out at 150 °F, and the milk starts out at 40 °F. We don’t expect the coffee to cool down to 40 °F or the milk to warm up to 150 °F. But could the coffee cool down to 69.5 °F and then go back up to 70 °F? Could the milk warm up to 70.5 °F and then cool back down to 70 °F?

I didn’t get a satisfactory answer to my childhood question until I was in college. Then I found out about Newton’s law of cooling. It says that the rate at which a warm body cools is proportional to the difference between its current temperature and the ambient temperature. This law can be written as a differential equation whose solution shows that the temperature of a warm body decreases exponentially to the ambient temperature. The temperature curve always slopes downward. It doesn’t wiggle even a little on its journey to room temperature. Cold bodies warm up the opposite way, exponentially approaching room temperature but never exceeding it.

In case this seems obvious, think about thermostats. They don’t work this way. Say the temperature in a room is 85 °F and you’d like it to be 72 °F, so you turn on the air conditioning. Will the temperature steadily lower to 72 °F? Not exactly. If you were to plot the temperature in the room over time and look at the graph from far enough away, it would look like it is steadily going down to the desired temperature. But if you look at the graph more closely, you’ll see wiggles. The AC may cool the room to a little below 72 °F, maybe to 70 °F. The AC would cut off and the temperature would rise to 72 °F. Unlike the cup of hot coffee, the AC will often overshoot its target, though not by too much. The temperature may feel constant, but it is not. It oscillates around the desired temperature.

Related: Consulting in differential equations

Springs, resistors, and harmonic means

Posted on by John

Harmonic mean has come up in a couple posts this week (with numbers and functions). This post will show how harmonic means come up in physical problems involving springs and resistors.

Suppose we have two springs in series with stiffness k1 and k2:

Then the combined stiffness k of the two springs satisfies 1/k = 1/k1 + 1/k2. Think about what this says in the extremes. If one of the springs were infinitely stiff, say k2 = ∞. Then k = k1. It would be as if the second spring were not there. Being infinitely stiff, we could think of it as an extension of the block it is attached to. Now think of one of the springs having no stiffness at all, say k1 = 0. Then k = 0. One mushy spring makes the combination mushy.

Next think of two springs in parallel:

Now the combined stiffness of the two springs is k = k1 + k2. Again think of the two extremes. If one spring is infinitely stiff, say k1 = ∞, then k = ∞ and the combination is infinitely stiff. And if one spring has no stiffness, say k2 = 0, then k = k1. We could imagine the spring with no stiffness isn’t there.

The stiffness of springs in series adds harmonically. The stiffness of the combination is half the harmonic mean of the two individual stiffnesses.

Electrical resistors combine in a way that is the opposite of mechanical springs. Resistors in parallel combine like springs in series, and vice versa.

If two resistors have resistance r1 and r2, the combined resistance r of the two resistors in parallel satisfies 1/r = 1/r1 + 1/r2. If one of the resistors has infinite resistance, say r2 = ∞, then r = r1. It would be as if the second resistor were not there. All electrons would flow through the first resistor.

If the two resistors were in series, then r = r1 + r2. If one resistor has infinite resistance, so does the combination. Electrons cannot flow through the combination if they cannot flow through one of the resistors. And if one resistor has zero resistance, say r2 = 0, then r = r1. Since the second resistor offers no resistance to the flow of electrons, it may as well not be there.

These physical problems illustrate why zeros as handled specially in the definition of means.

Image credit: Wikipedia

Two myths I learned in college: bathtub drains and airplane wings

Posted on by John

Here are two things I was taught in college that were absolutely wrong.

  • The Coriolis effect explains why bathtubs drain clockwise in the northern hemisphere.
  • The Bernoulli effect explains how planes fly.

These are not things that scientists believed at the time but were later disproved. They’re simply myths. (No doubt I’ve passed on a few myths to students over the years. If I can think of any, I’ll retract them here.)

The Coriolis effect does explain why cyclones rotate one way in the northern hemisphere and the opposite way in the southern hemisphere. The rotation of the earth influences the rotation of large bodies of fluid, like weather systems. However, a bathtub would need to be maybe a thousand miles in diameter before the Coriolis effect would determine how it drains. Bathtubs drain clockwise and counterclockwise in both hemispheres. Random forces such as sound in the air have more influence than the Coriolis effect on such small bodies of water.

The explanation  I learned in college for how airplanes fly involves the Bernoulli principle. The shape of a wing is such that air has to travel further over the top of the wing than under the bottom of the wing.

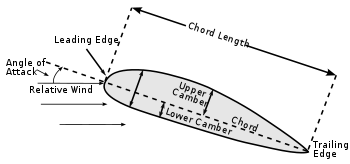airfoilSince air particles going across the top and bottom of the wing arrive at the trailing edge at the same time, the particles going over the top travel further and so are spread further apart. This results in lower pressure over the top of the wing and lifts the airplane.

There are a couple problems with this explanation. When the air particles split at the leading edge, why should the ones that go over the top and the ones that go under the bottom arrive at the trailing edge at the same time? In fact, they don’t. Also, while the Bernoulli effect does explain part of the lift on an airplane wing, the effect is an order of magnitude too small to account for why airplanes fly.

If the Bernoulli principle explains lift, how can an airplane fly upside-down? Wouldn’t the Bernoulli effect suck the plane down rather than lifting it up when you turn the wing over?

Here’s a  set of recordings from a lecture that debunks the Bernoulli effect myth and explains the real reason airplanes fly. Why airplanes fly: a modern myth. Part I, Part II.  There will be a Part III that hasn’t been released yet.

Update: Apparently these links have gone away.