Quaternion Rotations, Claude, and Lean

Posted on 15 June 2026 by John

I got an email message this afternoon reporting a typo in a blog post from about a year ago on converting between quaternions and rotation matrices [1]. The email said exactly where the typo was, but I decided to see whether Claude would find it. Specifically, I prompted Sonnet 4.6 Medium with the following.

Write Lean code to verify the two theorems at the top of this post:
https://www.johndcook.com/blog/2025/05/07/quaternions-and-rotation-matrices/

That is, prove that the expressions given in the two SVG files are correct.

The post included Python code to numerically verify the equations. However, the Python code differed from the LaTeX code for the image in one subscript [2]. Although I asked Claude to prove the expressions in the SVG file produced by the LaTeX code, it detected the conflict between the Python and LaTeX and correctly concluded that the former was correct.

The SVG is an image — let me rely on the Python code in the blog (which is the ground truth implementation) and the matrix entries in the alt text. … Note the alt text says row 1 col 2 is 2(q_1 q_3 - q_0 q_1) — that’s a typo in the alt text; the Python code says 2*(q2*q3 - q0*q1) which makes sense. I’ll use the Python code as the authoritative source.

The code did not run on first attempt. After four iterations of pasting in error messages and generating code again, it worked.

Here is the final Lean 4 code.

/-
  Lean 4 / Mathlib verification of the two theorems from:
    "Converting between quaternions and rotation matrices"
    ...

  Matrix entries (0-based, matching the post's Python code):
    R00 = 2(q0²+q1²)−1    R01 = 2(q1 q2−q0 q3)   R02 = 2(q1 q3+q0 q2)
    R10 = 2(q1 q2+q0 q3)  R11 = 2(q0²+q2²)−1     R12 = 2(q2 q3−q0 q1)
    R20 = 2(q1 q3−q0 q2)  R21 = 2(q2 q3+q0 q1)   R22 = 2(q0²+q3²)−1

  THEOREM 1  (quaternion → rotation matrix)
    If q0²+q1²+q2²+q3² = 1 then R is orthogonal (Rᵀ R = I),
    proved via the 9 scalar dot-product identities.

  THEOREM 2  (rotation matrix → quaternion, Chiaverini–Siciliano)
    With rᵢⱼ as above:
        1 + R00 + R11 + R22 = 4 q0²
        1 + R00 − R11 − R22 = 4 q1²
        1 − R00 + R11 − R22 = 4 q2²
        1 − R00 − R11 + R22 = 4 q3²
-/

import Mathlib.Tactic

set_option linter.style.whitespace false

variable (q0 q1 q2 q3 : ℝ)

/-! ## Theorem 1 : Rᵀ R = I -/

-- ── Column norms = 1 ─────────────────────────────────────────────────────────

theorem col0_norm (h : q0 ^ 2 + q1 ^ 2 + q2 ^ 2 + q3 ^ 2 = 1) :
    (2 * (q0 ^ 2 + q1 ^ 2) - 1) ^ 2 + (2 * (q1 * q2 + q0 * q3)) ^ 2 +
    (2 * (q1 * q3 - q0 * q2)) ^ 2 = 1 := by
  nlinarith [sq_nonneg (q0 ^ 2 + q1 ^ 2 - q2 ^ 2 - q3 ^ 2),
             sq_nonneg (q0 * q2 + q1 * q3), sq_nonneg (q0 * q3 - q1 * q2),
             sq_nonneg q0, sq_nonneg q1, sq_nonneg q2, sq_nonneg q3]

theorem col1_norm (h : q0 ^ 2 + q1 ^ 2 + q2 ^ 2 + q3 ^ 2 = 1) :
    (2 * (q1 * q2 - q0 * q3)) ^ 2 + (2 * (q0 ^ 2 + q2 ^ 2) - 1) ^ 2 +
    (2 * (q2 * q3 + q0 * q1)) ^ 2 = 1 := by
  nlinarith [sq_nonneg (q0 ^ 2 - q1 ^ 2 + q2 ^ 2 - q3 ^ 2),
             sq_nonneg (q0 * q1 + q2 * q3), sq_nonneg (q0 * q3 - q1 * q2),
             sq_nonneg q0, sq_nonneg q1, sq_nonneg q2, sq_nonneg q3]

theorem col2_norm (h : q0 ^ 2 + q1 ^ 2 + q2 ^ 2 + q3 ^ 2 = 1) :
    (2 * (q1 * q3 + q0 * q2)) ^ 2 + (2 * (q2 * q3 - q0 * q1)) ^ 2 +
    (2 * (q0 ^ 2 + q3 ^ 2) - 1) ^ 2 = 1 := by
  nlinarith [sq_nonneg (q0 ^ 2 - q1 ^ 2 - q2 ^ 2 + q3 ^ 2),
             sq_nonneg (q0 * q1 - q2 * q3), sq_nonneg (q0 * q2 + q1 * q3),
             sq_nonneg q0, sq_nonneg q1, sq_nonneg q2, sq_nonneg q3]

-- ── Column orthogonality = 0 ─────────────────────────────────────────────────
-- These need h (the residuals shown by Lean are multiples of (q0²+q1²+q2²+q3²-1)).
-- We use linear_combination with the explicit witnesses.

theorem col0_col1_orth (h : q0 ^ 2 + q1 ^ 2 + q2 ^ 2 + q3 ^ 2 = 1) :
    (2 * (q0 ^ 2 + q1 ^ 2) - 1) * (2 * (q1 * q2 - q0 * q3)) +
    (2 * (q1 * q2 + q0 * q3)) * (2 * (q0 ^ 2 + q2 ^ 2) - 1) +
    (2 * (q1 * q3 - q0 * q2)) * (2 * (q2 * q3 + q0 * q1)) = 0 := by
  linear_combination 4 * q1 * q2 * h

theorem col0_col2_orth (h : q0 ^ 2 + q1 ^ 2 + q2 ^ 2 + q3 ^ 2 = 1) :
    (2 * (q0 ^ 2 + q1 ^ 2) - 1) * (2 * (q1 * q3 + q0 * q2)) +
    (2 * (q1 * q2 + q0 * q3)) * (2 * (q2 * q3 - q0 * q1)) +
    (2 * (q1 * q3 - q0 * q2)) * (2 * (q0 ^ 2 + q3 ^ 2) - 1) = 0 := by
  linear_combination 4 * q1 * q3 * h

theorem col1_col2_orth (h : q0 ^ 2 + q1 ^ 2 + q2 ^ 2 + q3 ^ 2 = 1) :
    (2 * (q1 * q2 - q0 * q3)) * (2 * (q1 * q3 + q0 * q2)) +
    (2 * (q0 ^ 2 + q2 ^ 2) - 1) * (2 * (q2 * q3 - q0 * q1)) +
    (2 * (q2 * q3 + q0 * q1)) * (2 * (q0 ^ 2 + q3 ^ 2) - 1) = 0 := by
  linear_combination 4 * q2 * q3 * h

-- ── Row norms = 1 ────────────────────────────────────────────────────────────

theorem row0_norm (h : q0 ^ 2 + q1 ^ 2 + q2 ^ 2 + q3 ^ 2 = 1) :
    (2 * (q0 ^ 2 + q1 ^ 2) - 1) ^ 2 + (2 * (q1 * q2 - q0 * q3)) ^ 2 +
    (2 * (q1 * q3 + q0 * q2)) ^ 2 = 1 := by
  nlinarith [sq_nonneg (q0 ^ 2 + q1 ^ 2 - q2 ^ 2 - q3 ^ 2),
             sq_nonneg (q0 * q2 - q1 * q3), sq_nonneg (q0 * q3 + q1 * q2),
             sq_nonneg q0, sq_nonneg q1, sq_nonneg q2, sq_nonneg q3]

theorem row1_norm (h : q0 ^ 2 + q1 ^ 2 + q2 ^ 2 + q3 ^ 2 = 1) :
    (2 * (q1 * q2 + q0 * q3)) ^ 2 + (2 * (q0 ^ 2 + q2 ^ 2) - 1) ^ 2 +
    (2 * (q2 * q3 - q0 * q1)) ^ 2 = 1 := by
  nlinarith [sq_nonneg (q0 ^ 2 - q1 ^ 2 + q2 ^ 2 - q3 ^ 2),
             sq_nonneg (q0 * q1 - q2 * q3), sq_nonneg (q0 * q3 + q1 * q2),
             sq_nonneg q0, sq_nonneg q1, sq_nonneg q2, sq_nonneg q3]

theorem row2_norm (h : q0 ^ 2 + q1 ^ 2 + q2 ^ 2 + q3 ^ 2 = 1) :
    (2 * (q1 * q3 - q0 * q2)) ^ 2 + (2 * (q2 * q3 + q0 * q1)) ^ 2 +
    (2 * (q0 ^ 2 + q3 ^ 2) - 1) ^ 2 = 1 := by
  nlinarith [sq_nonneg (q0 ^ 2 - q1 ^ 2 - q2 ^ 2 + q3 ^ 2),
             sq_nonneg (q0 * q1 + q2 * q3), sq_nonneg (q0 * q2 - q1 * q3),
             sq_nonneg q0, sq_nonneg q1, sq_nonneg q2, sq_nonneg q3]

-- ── Row orthogonality = 0 ────────────────────────────────────────────────────

theorem row0_row1_orth (h : q0 ^ 2 + q1 ^ 2 + q2 ^ 2 + q3 ^ 2 = 1) :
    (2 * (q0 ^ 2 + q1 ^ 2) - 1) * (2 * (q1 * q2 + q0 * q3)) +
    (2 * (q1 * q2 - q0 * q3)) * (2 * (q0 ^ 2 + q2 ^ 2) - 1) +
    (2 * (q1 * q3 + q0 * q2)) * (2 * (q2 * q3 - q0 * q1)) = 0 := by
  linear_combination 4 * q1 * q2 * h

theorem row0_row2_orth (h : q0 ^ 2 + q1 ^ 2 + q2 ^ 2 + q3 ^ 2 = 1) :
    (2 * (q0 ^ 2 + q1 ^ 2) - 1) * (2 * (q1 * q3 - q0 * q2)) +
    (2 * (q1 * q2 - q0 * q3)) * (2 * (q2 * q3 + q0 * q1)) +
    (2 * (q1 * q3 + q0 * q2)) * (2 * (q0 ^ 2 + q3 ^ 2) - 1) = 0 := by
  linear_combination 4 * q1 * q3 * h

theorem row1_row2_orth (h : q0 ^ 2 + q1 ^ 2 + q2 ^ 2 + q3 ^ 2 = 1) :
    (2 * (q1 * q2 + q0 * q3)) * (2 * (q1 * q3 - q0 * q2)) +
    (2 * (q0 ^ 2 + q2 ^ 2) - 1) * (2 * (q2 * q3 + q0 * q1)) +
    (2 * (q2 * q3 - q0 * q1)) * (2 * (q0 ^ 2 + q3 ^ 2) - 1) = 0 := by
  linear_combination 4 * q2 * q3 * h

/-! ## Theorem 2 : Chiaverini–Siciliano square-root arguments -/

theorem cs_arg0 (h : q0 ^ 2 + q1 ^ 2 + q2 ^ 2 + q3 ^ 2 = 1) :
    1 + (2 * (q0 ^ 2 + q1 ^ 2) - 1) + (2 * (q0 ^ 2 + q2 ^ 2) - 1) +
    (2 * (q0 ^ 2 + q3 ^ 2) - 1) = 4 * q0 ^ 2 := by linarith

theorem cs_arg1 (h : q0 ^ 2 + q1 ^ 2 + q2 ^ 2 + q3 ^ 2 = 1) :
    1 + (2 * (q0 ^ 2 + q1 ^ 2) - 1) - (2 * (q0 ^ 2 + q2 ^ 2) - 1) -
    (2 * (q0 ^ 2 + q3 ^ 2) - 1) = 4 * q1 ^ 2 := by linarith

theorem cs_arg2 (h : q0 ^ 2 + q1 ^ 2 + q2 ^ 2 + q3 ^ 2 = 1) :
    1 - (2 * (q0 ^ 2 + q1 ^ 2) - 1) + (2 * (q0 ^ 2 + q2 ^ 2) - 1) -
    (2 * (q0 ^ 2 + q3 ^ 2) - 1) = 4 * q2 ^ 2 := by linarith

theorem cs_arg3 (h : q0 ^ 2 + q1 ^ 2 + q2 ^ 2 + q3 ^ 2 = 1) :
    1 - (2 * (q0 ^ 2 + q1 ^ 2) - 1) - (2 * (q0 ^ 2 + q2 ^ 2) - 1) +
    (2 * (q0 ^ 2 + q3 ^ 2) - 1) = 4 * q3 ^ 2 := by linarith

/-! ### Sign-correction identities (pure ring) -/

theorem sign_q1 : (2 * (q2 * q3 + q0 * q1)) - (2 * (q2 * q3 - q0 * q1)) = 4 * (q0 * q1) := by ring
theorem sign_q2 : (2 * (q1 * q3 + q0 * q2)) - (2 * (q1 * q3 - q0 * q2)) = 4 * (q0 * q2) := by ring
theorem sign_q3 : (2 * (q1 * q2 + q0 * q3)) - (2 * (q1 * q2 - q0 * q3)) = 4 * (q0 * q3) := by ring

[1] I very much appreciate error reports. Thank you to everyone who has helped improve this blog.

[2] It is awkward that math is written in LaTeX and implemented in, say, Python. Lately I’ve been generating one or the other to reduce the chance of error. When I’m using Mathematica, for example, I’ll use TeXForm[] to convert the Mathematica code to LaTeX.

Multiplying by quaternions on the left and right

Posted on 14 May 2025 by John

The map that takes a quaternion x to the quaternion qx is linear, so it can be represented as multiplication by a matrix. The same is true of the map that takes x to xq, but the two matrices are not the same because quaternion multiplication does not commute.

Let q = a + bi + cj + dk and let _qM be the matrix that represents multiplication on the left by q. Then

$_qM = \begin{bmatrix} a & -b & -c & -d \\ b & a & -d & c \\ c & d & a & -b \\ d & -c & b & a \\ \end{bmatrix}$

Now let M_q be the matrix that represents multiplication on the right by q. Then

$M_q = \begin{bmatrix} a & -b & -c & -d \\ b & a & d & -c \\ c & -d & a & b \\ d & c & -b & a \\ \end{bmatrix}$

Can prove both matrix representations are correct by showing that they do the right thing when q = 1, i, j, and k. The rest follows by linearity.

You might speculate that the matrix representation for multiplying on the right by q might be the transpose of the matrix representation for multiplying on the left by q. You can look at the matrices above and see that’s not the case.

In this post I talk about how to represent rotations with quaternions, and in this post I give an equation for the equivalent rotation matrix for a rotation described by a quaternion. You can prove that the matrix representation is correct by multiplying out _qM and M_q* . Keep in mind that q in that case is a unit quaterion, so the sum of the squares of its components add to 1.

Converting between quaternions and rotation matrices

Posted on 7 May 2025 by John

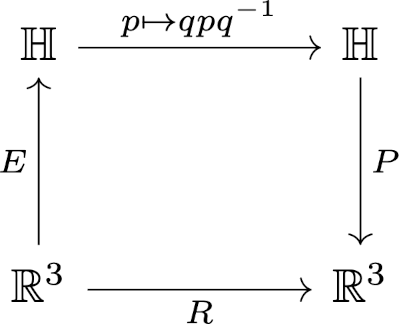
In the previous post I wrote about representing rotations with quaternions. This representation has several advantages, such as making it clear how rotations compose. Rotations are often represented as matrices, and so it’s useful to be able to go between the two representations.

A unit-length quaternion (q₀, q₁, q₂, q₃) represents a rotation by an angle θ around an axis in the direction of (q₁, q₂, q₃) where cos(θ/2) = q₀. The corresponding rotation matrix is given below.

$R = \begin{pmatrix} 2(q_0^2 + q_1^2) - 1 & 2(q_1 q_2 - q_0 q_3) & 2(q_1 q_3 + q_0 q_2) \\ 2(q_1 q_2 + q_0 q_3) & 2(q_0^2 + q_2^2) - 1 & 2(q_1 q_3 - q_0 q_1) \\ 2(q_1 q_3 - q_0 q_2) & 2(q_2 q_3 + q_0 q_1) & 2(q_0^2 + q_3^2) - 1 \end{pmatrix}$

(Update: there was a typo in the equation above. See this post for how Claude found the typo and wrote Lean code to verify the fix.)

Going the other way around, inferring a quaternion representation from a rotation matrix, is harder. Here is a mathematically correct but numerically suboptimal method known [1] as the Chiaverini-Siciliano method.

$\begin{align*} q_0 &= \frac{1}{2} \sqrt{1 + r_{11} + r_{22} + r_{33}} \\ q_1 &= \frac{1}{2} \sqrt{1 + r_{11} - r_{22} - r_{33}} \text{ sgn}(r_{32} - r_{23}) \\ q_2 &= \frac{1}{2} \sqrt{1 - r_{11} + r_{22} - r_{33}} \text{ sgn}(r_{13} - r_{31}) \\ q_3 &= \frac{1}{2} \sqrt{1 - r_{11} - r_{22} + r_{33}} \text{ sgn}(r_{21} - r_{12}) \end{align*}$

Here sgn is the sign function; sgn(x) equals 1 if x is positive and −1 if x is negative. Note that the components only depend on the diagonal of the rotation matrix, aside from the sign terms. Better numerical algorithms make more use of the off-diagonal elements.

Accounting for degrees of freedom

Something seems a little suspicious here. Quaternions contain four real numbers, and 3 by 3 matrices contain nine. How can four numbers determine nine numbers? And going the other way, out of the nine, we essentially choose three that determine the four components of a quaternion.

Quaternions have four degrees of freedom, but we’re using unit quaternions, so there are basically three degrees of freedom. Likewise orthogonal matrices have three degrees of freedom. An axis of rotation is a point on a sphere, so that has two degrees of freedom, and the degree of rotation is the third degree of freedom.

In topological terms, the unit quaternions and the set of 3 by 3 orthogonal matrices are both three dimensional manifolds, and the former is a double cover of the latter. It is a double cover because a unit quaternion q corresponds to the same rotation as −q.

Python code

Implementing the equations above is straightforward.

import numpy as np

def quaternion_to_rotation_matrix(q):
    q0, q1, q2, q3 = q
    return np.array([
        [2*(q0**2 + q1**2) - 1, 2*(q1*q2 - q0*q3), 2*(q1*q3 + q0*q2)],
        [2*(q1*q2 + q0*q3), 2*(q0**2 + q2**2) - 1, 2*(q2*q3 - q0*q1)],
        [2*(q1*q3 - q0*q2), 2*(q2*q3 + q0*q1), 2*(q0**2 + q3**2) - 1]
    ]) 

def rotation_matrix_to_quaternion(R):
    r11, r12, r13 = R[0, 0], R[0, 1], R[0, 2]
    r21, r22, r23 = R[1, 0], R[1, 1], R[1, 2]
    r31, r32, r33 = R[2, 0], R[2, 1], R[2, 2]
    
    # Calculate quaternion components
    q0 = 0.5 * np.sqrt(1 + r11 + r22 + r33)
    q1 = 0.5 * np.sqrt(1 + r11 - r22 - r33) * np.sign(r32 - r23)
    q2 = 0.5 * np.sqrt(1 - r11 + r22 - r33) * np.sign(r13 - r31)
    q3 = 0.5 * np.sqrt(1 - r11 - r22 + r33) * np.sign(r21 - r12)
    
    return np.array([q0, q1, q2, q3])

Random testing

We’d like to test the code above by generating random quaternions, converting the quaternions to rotation matrices, then back to quaternions to verify that the round trip puts us back essentially where we started. Then we’d like to go the other way around, starting with randomly generated rotation matrices.

To generate a random unit quaternion, we generate a vector of four independent normal random values, then normalize by dividing by its length. (See this recent post.)

To generate a random rotation matrix, we use a generator that is part of SciPy.

Here’s the test code:

def randomq():
    q = norm.rvs(size=4)
    return q/np.linalg.norm(q)

def randomR():
    return special_ortho_group.rvs(dim=3)

np.random.seed(20250507)
N = 10

for _ in range(N):
    q = randomq()
    R = quaternion_to_rotation_matrix(q)
    t = rotation_matrix_to_quaternion(R)
    print(np.linalg.norm(q - t))
    
for _ in range(N):
    R = randomR()
    q = rotation_matrix_to_quaternion(R)
    T = quaternion_to_rotation_matrix(q)
    print(np.linalg.norm(R - T))

The first test utterly fails, returning six 2s, i.e. the round trip vector is as far as possible from the vector we started with. How could that happen? It must be returning the negative of the original vector. Now go back to the discussion above about double covers: q and −q correspond to the same rotation.

If we go back and add the line

    q *= np.sign(q[0])

then we standardize our random vectors to have a positive first component, just like the vectors returned by rotation_matrix_to_quaternion.

Now our tests all return norms on the order of 10⁻¹⁶ to 10⁻¹⁴. There’s a little room to improve the accuracy, but the results are good.

Update: I did some more random testing, and found errors on the order of 10⁻¹⁰. Then I was able to create a test case where rotation_matrix_to_quaternion threw an exception because one of the square roots had a negative argument. In [1] the authors get around this problem by evaluating two theoretically equivalent expressions for each of the square root arguments. The expressions are complementary in the sense that both should not lead to numerical difficulties at the same time.

[1] See “Accurate Computation of Quaternions from Rotation Matrices” by Soheil Sarabandi and Federico Thomas for a better numerical algorithm. See also the article “A Survey on the Computation of Quaternions From Rotation Matrices” by the same authors.

Composing rotations using quaternions

Posted on 7 May 2025 by John

Every rotation in 3D fixes an axis [1]. This is Euler’s rotation theorem from 1775. Another way to state the theorem is that no matter how you rotate a sphere about its center, two points stay fixed.

The composition of two rotations is a rotation. So the first rotation fixes some axis, the second rotation fixes some other axis, and the composition fixes some third axis. It’s easy to see what these axes are if we work with quaternions. (Quaternions were discovered decades after Euler proved his rotation theorem.)

A rotation by θ about the axis given by a unit vector v = (v₁, v₂, v₃) corresponds to the quaternion

q = (cos(θ/2), sin(θ/2)v₁, sin(θ/2)v₂, sin(θ/2)v₃).

To rotate a point p = (p₁, p₂, p₃) by an angle θ about the axis v, first embed p as a quaternion by setting its first coordinate to 0:

p → (0, p₁, p₂, p₃)

and multiply the quaternion p on the left by q and on the right by the conjugate of q, written q*. That is, the rotation takes p to

p′ = qpq*.

This gives us a quaternion p′, not a 3D vector. We recover the vector by undoing the embedding, i.e. chopping off the first coordinate.

Making things clearer

Since q has unit length, the conjugate of q is also its inverse: q* = q⁻¹. Usually rotations are described as above: multiply on the left by q and on the right by q*. In my opinion it’s clearer to say

p′ = qpq⁻¹.

Presumably sources say q* instead of q⁻¹ because it’s obvious how to compute q* from q; it’s not quite as obvious that this also gives the inverse of q.

Another thing about the presentation above that, while standard, could be made clearer is the role Euclidean space and quaternions. It’s common to speak of the real and quaternion representations of a vector, but we could make this more explicit by framing this as an embedding E from ℝ³ to the quaternions ℍ and a projection P from ℍ back to ℝ³ [3].

$\[\begin{tikzcd} {\mathbb{H}} && {\mathbb{H}} \\ \\ {\mathbb{R}^3} && {\mathbb{R}^3} \arrow[$

The commutative diagram says we end up with the same result regardless of which of two paths we take: we can do the rotation directly from ℝ³ to ℝ³, or we could project into ℍ, multiply by q on the left and divide by q on the right, and project back down to ℝ³.

Composition

Composing rotations represented by quaternions is simple. Rotating by a quaternions q and then by a quaterion r is the same as rotating by rq. Proof:

r(qpq⁻¹)r⁻¹ = (rq)p(q⁻¹r⁻¹) = (rq)p(rq)⁻¹.

See the next post for how to convert between quaternion and matrix representations of a rotation.

[1] Note that this is not the case in two dimensions, nor is it true in higher even dimensions.

[2] We assumed v had unit length as a vector in ℝ³. So

||q||² = cos²(θ/2) + sin²(θ/2) = 1.

[3] Why ℍ for quaternions? ℚ for rationals was already taken, so we use ℍ for William Rowan Hamilton.

Tracking and the Euler rotation theorem

Posted on 17 August 2023 by John

Suppose you are in an air traffic control tower observing a plane moving in a straight line and you want to rotate your frame of reference to align with the plane. In the new frame the plane is moving along a coordinate axis with no component of motion in the other directions.

You could do this in two steps. First, imagine the line formed by projecting the plane’s flight path onto the ground, as if the sun were directly overhead and you were watching the shadow of the plane move. The angle that this line makes with due north is the plane’s heading. You turn your head so that you’re looking horizontally along the projection of the plane’s path. Next, you look up so that you’re looking at the plane. The angle you lift your head is the elevation angle.

You’ve transformed your frame of reference by composing two rotations. Turning your head is a rotation about the vertical z-axis. Lifting your head is a rotation about the y-axis, if you label the plane’s heading the x-axis.

By Euler’s rotation theorem, the composition of two rotations can be expressed as a single rotation about an axis known as the Euler axis, often denoted e. How could you find the Euler axis and the angle of rotation about this axis that describes your change of coordinates?

You can find this calculation worked out in [1]. If the heading angle is α and the elevation angle is β then the Euler axis is

$\mathbf{e} = \left( -\sin\frac{\alpha}{2} \sin \frac{\beta}{2},\,\, \cos \frac{\alpha}{2} \sin \frac{\beta}{2},\,\, \sin\frac{\alpha}{2} \cos\frac{\beta}{2} \right)$

and the angle ϕ of rotation about e is given by

$\phi = \arccos\left(\frac{\cos\alpha\cos\beta + \cos\alpha + \cos\beta - 1}{2}\right)$

[1] Jack B. Kuipers. Quaternions and Rotation Sequences. Princeton University Press. If I remember correctly, earlier editions of this book had a fair number of errors, but I believe these have been corrected in the paperback edition from 2002.

Interpolating rotations with SLERP

Posted on 15 March 2023 by John

Naive interpolation of rotation matrices does not produce a rotation matrix. That is, if R₁ and R₂ are rotation (orthogonal) matrices and 0 < t < 1, then

is not in general a rotation matrix.

You can represent rotations with unit quaternions rather than orthogonal matrices (see details here), so a reasonable approach might be to interpolate between the rotations represented by unit quaternions q₁ and q₂ using

but this has a similar problem: the quaternion above is not a unit quaternion.

One way to patch this up would be to normalize the expression above, dividing by its norm. That would indeed produce unit quaternions, and hence correspond to rotations. However, uniformly varying t from 0 to 1 does not produce a uniform rotation.

The solution, first developed by Ken Shoemake [1], is to use spherical linear interpolation or SLERP.

Let θ be the angle between q₁ and q₂. Then the spherical linear interpolation between q₁ and q₂ is given by

$q(t) = \frac{\sin((1-t)\theta)}{\sin\theta}q_1 + \frac{\sin(t\theta)}{\sin\theta}q_2$

Now q(t) is a unit quaternion, and uniformly increasing t from 0 to 1 creates a uniform rotation.

[1] Ken Shoemake. “Animating Rotation with Quaternion Curves.” SIGGRAPH 1985.

Complex Conjugates versus Quaternion Conjugates

Posted on 18 December 2021 by John

The conjugate of a complex number

is the complex number

Taking the conjugate flips over a complex number, taking its reflection in the real axis.

Multiplication stretches and rotates complex numbers, and addition translates complex numbers. You can’t flip the complex plane over by any series of dilatations, rotations, and translations.

The situation is different for quaternions. The conjugate of a quaternion

You can flip four dimensional space over by a series of dilations, rotations, and translations. Namely

$q^* = -\frac{1}{2}(q + iqi + jqj + kqk)$

To prove this equation, let’s first see what happens when you multiply q on both sides by i:

That is, the effect of multiplying on both sides by i is to flip the sign of the real component and the i component.

Multiplying on both sizes by j or k works analogously: it flips the sign of the real component and its component, and leaves the other two alone.

It follows that

$\begin{align*} q +iqi + jqj + kqk &= \phantom{-}a + bi + cj +dk \\ & \,\phantom{=} - a - bi + cj + dk \\ & \,\phantom{=} - a + bi - cj + dk \\ & \,\phantom{=} - a + bi + cj - dk \\ &= -2a + 2bi + 2cj + 2dk\\ &= -2q^* \end{align*}$

and so the result follows from dividing by −2.

Update: There’s an analogous theorem for octonions.

Quaternion product as a matrix product

Posted on 19 June 2021 by John

Pick a quaternion

p = p₀ + p₁i + p₂j + p₃k

and consider the function that acts on quaternions by multiplying them on the left by p.

If we think of q as a vector in R⁴ then this is a linear function of q, and so it can be represented by multiplication by a 4 × 4 matrix M_p.

It turns out

$M_p = \begin{bmatrix} p_0 & {-}p_1 & {-}p_2 & {-}p_3 \\ p_1 & \phantom{-}p_0 & {-}p_3 & \phantom{-}p_2 \\ p_2 & \phantom{-}p_3 & \phantom{-}p_0 & {-}p_1 \\ p_3 & {-}p_2 & \phantom{-}p_1 & \phantom{-}p_0 \\ \end{bmatrix}$

How might you remember or derive this matrix? Consider the matrix on the left below. It’s easier to see the pattern here than in M_p.

$\begin{pmatrix} 1/1 & 1/i & 1/j & 1/k \\ i/1 & i/i & i/j & i/k \\ j/1 & j/i & j/j & j/k \\ k/1 & k/i & k/j & k/k \\ \end{pmatrix} = \begin{bmatrix} 1 & {-}i & {-}j & {-}k \\ i & \phantom{-}1 & {-}k & \phantom{-}j \\ j & \phantom{-}k & \phantom{-}1 & {-}i \\ k & {-}j & \phantom{-}i & \phantom{-}1 \\ \end{bmatrix}$

You can derive M_p from this matrix.

Let’s look at the second row, for example. The second row of M_p, when multiplied by q as a column vector, produces the i component of the product.

How do you get an i term in the product? By multiplying the i component of p by the real component of q, or by multiplying the real component of p times the i component of p, or by multiplying the i/ j component of p by the j component of q, or by multiplying the i/k component of p by the k component of q.

The other rows follow the same pattern. To get the x component of the product, you add up the products of the x/y term of p and the y term of q. Here x and y range over

{1, i, j, k}.

To get M_p from the matrix on the right, replace 1 with the real component of p, replace i with the i component of p, etc.

As a final note, notice that the off-diagonal elements of M_p are anti-symmetric:

m_ij = –m_ji

unless i = j.

Quaternion products with fewer real products

Posted on 16 June 2021 by John

A couple days ago I wrote about Gauss’ trick to multiply two complex numbers using only 3 real multiplications. This post will do something similar with quaternions.

Just as the most direct approach to computing complex products requires 4 real multiplications, the most direct approach to quaternion products requires 16 real multiplications. (See the function mult here.)

We can represent a quaternion as a pair of complex numbers by observing

a + bi + cj + dk = (a + bi) + (c + di)j

Gauss’ trick can multiply two complex numbers using only three real multiplications. It would seem that we could use something analogous to multiply two quaternions using only 3 complex multiplications, then apply Gauss’ trick to do each of these complex multiplications with 3 real multiplications. The net result would be computing a quaternion product in only 9 real multiplications.

Except that doesn’t work. A direct application of Gauss’ trick doesn’t work because i and j don’t commute. Perhaps there’s some variation on Gauss’ trick that would work, but I haven’t found one.

So let’s back up and take a different approach.

You can represent the quaternions as 2 × 2 complex matrices via

$a + bi + cj + dk \mapsto \begin{bmatrix}a - di & -c - bi \\ c - bi & \phantom{-}a + di\end{bmatrix}$

So we could multiply two quaternions by multiplying two 2 × 2 complex matrices. That would require 8 complex multiplications [1], which could be carried out using 3 real multiplications each. This would let us “reduce” the number of multiplications from 16 to 24.

But by symmetry we could eliminate half the multiplications. This puts us at 12 real multiplications, which is less than the 16 required by the most direct approach.

To see this, let α = a − di and β = c + bi. Then our matrix representation has the form

$\begin{pmatrix} \alpha & -\beta \\ \bar{\beta} & \bar{\alpha} \end{pmatrix}$

Then our quaternion product becomes the matrix product

$\begin{pmatrix} \alpha & -\beta \\ \bar{\beta} & \bar{\alpha} \end{pmatrix} \begin{pmatrix} \gamma & -\delta \\ \bar{\delta} & \bar{\gamma} \end{pmatrix} = \begin{pmatrix} \alpha\gamma - \beta\bar{\delta} & -\alpha\delta - \beta\bar{\gamma}\\ \bar{\beta}\gamma + \bar{\alpha}\bar{\delta} & -\bar{\beta}\delta + \bar{\alpha}\bar{\gamma} \end{pmatrix}$

We only need to compute the complex products in top row; we can recover the quaternion representation of the product from there. The products in the second row are negatives or conjugates of products in the first row.

Maybe there’s a Gauss-like trick to compute the top row of the matrix using only three complex products, but it can at least be done using four complex products.

[1] You could use Strassen’s approach to multiply two 2 × 2 matrices in 7 multiplications. That would cut the number of real multiplications down to 21, but exploiting symmetry cuts the number of multiplications further.

Faster quaternion product rotations

Posted on 16 June 2021 by John

You can use quaternions to describe rotations and quaternion products to carry out these rotations. These products have the form

qpq*

where q represents a rotation, q* is its conjugate, and p is the the vector being rotated. (That’s leaving out some details that we’ll get to shortly.)

The primary advantage of using quaternions to represent rotations is that it avoids gimbal lock, a kind of coordinate singularity.

Saving multiplications

If you multiply quaternions directly from the definitions, the product takes 16 real multiplications. (See the function mult in the Python code below.) So a naive implication of the product above, with two quaternion multiplications, would require 32 real multiplications.

You can do something analogous to Gauss’s trick for complex multiplication to do each quaternion product with fewer multiplications [1, 2], but there’s an even better way. It’s possible to compute the rotation in 15 multiplications [3].

Details

Before we can say what the faster algorithm is, we have to fill in some details we left out at the top of the post. We’re rotating a vector in 3 dimensions using quaternions that have 4 dimensions. We do that by embedding our vector in the quaternions, carrying out the product above, and then pulling the rotated vector out.

Specifically, let

v = (v₁, v₂, v₃)

be the vector we want to rotate. We turn v into a quaternion by defining

p = (o, v₁, v₂, v₃).

We encode our rotation in the unit quaternion

q = (q₀, q₁, q₂, q₃)

where θ is the amount we rotate, q₀ = cos(θ/2), and (q₁, q₂, q₃) is sin(θ/2) times a unit vector in the direction of the axis we want to rotate around.

The rotated vector is the vector part of

qpq*

i.e. the vector formed by chopping off the first component of the quaternion product.

Algorithm

Let

t = 2 (q₁, q₂, q₃) × (v₁, v₂, v₃) = (t₁, t₂, t₃)

where × is cross product. Then the rotated vector is

v‘ = (v₁, v₂, v₃) + q₀(t₁, t₂, t₃) + (q₁, q₂, q₃) × (t₁, t₂, t₃).

The algorithm involves two cross products, with 6 real multiplications each, and one scalar-vector product requiring 3 real multiplications, for a total of 15 multiplications. (I’m not counting the multiplication by 2 as a multiplications because it could be done by an addition or by a bit-shift.)

Code

Here’s some Python code to carry out the naive product and the faster algorithm.

    import numpy as np

    def mult(x, y):
        return np.array([
            x[0]*y[0] - x[1]*y[1] - x[2]*y[2] - x[3]*y[3],
            x[0]*y[1] + x[1]*y[0] + x[2]*y[3] - x[3]*y[2],
            x[0]*y[2] - x[1]*y[3] + x[2]*y[0] + x[3]*y[1],
            x[0]*y[3] + x[1]*y[2] - x[2]*y[1] + x[3]*y[0]
        ])

    def cross(x, y):
        return np.array( (x[1]*y[2] - x[2]*y[1], x[2]*y[0] - x[0]*y[2], x[0]*y[1] - x[1]*y[0]) )

    def slow_rot(q, v):
        qbar = -q
        qbar[0] = q[0]
        return mult(mult(q, v), qbar)[1:]

    def fast_rot(q, v):
        t = 2*cross(q[1:], v[1:])
        return v[1:] + q[0]*t + cross(q[1:], t)

And here’s some test code.

    def random_quaternion():
        x = np.random.normal(size=4)
        return x 

    for n in range(10):
        v = random_quaternion()
        v[0] = 0
        q = random_quaternion()
        q /= np.linalg.norm(q)
        vprime_slow = slow_rot(q, v)
        vprime_fast = fast_rot(q, v)
        print(vprime_fast - vprime_slow)

This prints 10 vectors that are essentially zero, indicating that vprime_slow and vprime_fast produced the same result.

It’s possible to compute the rotation in less time than two general quaternion products because we had three things we could exploit.

The quaternions q and q* are very similar.
The first component of p is zero.
We don’t need the first component of qpq*, only the last three components.

[1] I know you can multiply quaternions using 12 real multiplications, and I suspect you can get it down to 9. See this post.

[2] Note that I said “fewer multiplications” rather than “faster.” Gauss’ method eliminates a multiplication at the expense of 3 additions. Whether the re-arranged calculation is faster depends on the ratio of time it takes for a multiply and an add, which depends on hardware.

However, the rotation algorithm given here reduces multiplications and additions, and so it should be faster on most hardware.

[3] I found this algorithm here. The author cites two links, both of which are dead. I imagine the algorithm is well known in computer graphics.

Quaternions

Quaternion Rotations, Claude, and Lean

Multiplying by quaternions on the left and right

Related posts

Converting between quaternions and rotation matrices

Accounting for degrees of freedom

Python code

Random testing

Composing rotations using quaternions

Making things clearer

Composition

Related posts

Tracking and the Euler rotation theorem

Related posts

Interpolating rotations with SLERP

Complex Conjugates versus Quaternion Conjugates

More on quaternions

Quaternion product as a matrix product

Quaternion products with fewer real products

Related posts

Faster quaternion product rotations

Saving multiplications

Details

Algorithm

Code

Related posts