Quaternions

How close is octonion multiplication to being associative?

Posted on by John

Quaternion multiplication is associative but not commutative. An earlier post looked at the average size of the commutator xy – yx as a measure of how far quaternion multiplication is from being commutative.

This post looks at an analogous question for octonions. Octonion multiplication is neither commutative nor associative. So in this post we look at the associator of three octonions (xy)z – x(yz) as a measure of how far octonion multiplication is from being associative.

(A post from yesterday looked at how close octonion multiplication comes to being associative in an algebraic sense, looking at weak forms of associativity. This post looks at how close multiplication comes to being associative in an analytical sense, looking at norm distances rather than algebraic identities.)

We will use a simulation to look at the average norm of the octonion associator over the octionions of unit length, analogous to the earlier post that looked at the commutator of the quaternions. We developed code for octonion multiplication in the previous post and will reuse that code here. We also developed code for generating random unit-length octonions in the same post.

Here’s code to find the average norm of the associator and plot a histogram of its values.

    
    import matplotlib.pyplot as plt

    # omult is octonion multiplication. 
    # See previous post.
    def associator(x, y, z):
        return omult(omult(x, y), z) - 
               omult(x, omult(y, z))

    N = 100000
    s = 0
    h = np.zeros(N)
    for n in range(N):
        x = random_unit_octonion()
        y = random_unit_octonion()
        z = random_unit_octonion()    
        t = norm(associator(x, y, z))
        s += t
        h[n] = t

    print(s/N)
    plt.hist(h, bins=50)
    plt.show()

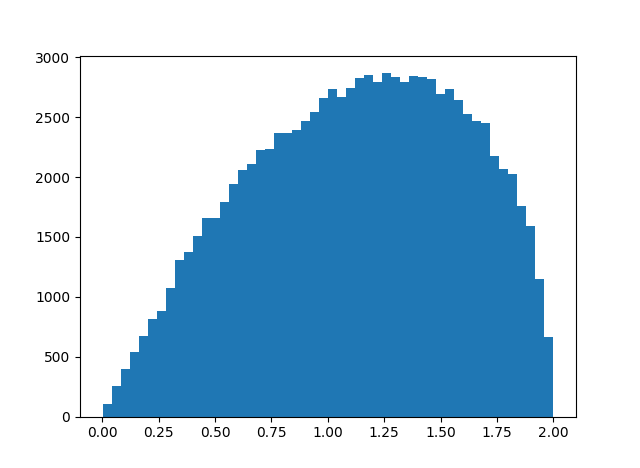
This gives an average of 1.095 and the histogram below.

histogram of octonion associator norm values

Update: Greg Egan calculated the exact mean value for the norm of the associator to be 147456/(42875 π) ≈ 1.0947336. Here are the details.

How far is xy from yx on average for quaternions?

Posted on by John

Given two quaternions x and y, the product xy might equal the product yx, but in general the two results are different.

How different are xy and yx on average? That is, if you selected quaternions x and y at random, how big would you expect the difference xy – yx to be? Since this difference would increase proportionately if you increased the length of x or y, we can just consider quaternions of norm 1. In other words, we’re looking at the size of xy – yx relative to the size of xy.

Here’s simulation code to explore our question.

    import numpy as np
    
    def random_unit_quaternion():
        x = np.random.normal(size=4)
        return x / np.linalg.norm(x)
    
    def mult(x, y):
        return np.array([
            x[0]*y[0] - x[1]*y[1] - x[2]*y[2] - x[3]*y[3],
            x[0]*y[1] + x[1]*y[0] + x[2]*y[3] - x[3]*y[2],
            x[0]*y[2] - x[1]*y[3] + x[2]*y[0] + x[3]*y[1],
            x[0]*y[3] + x[1]*y[2] - x[2]*y[1] + x[3]*y[0]
        ])
    
    
    N = 10000
    s = 0
    for _ in range(N):
        x = random_unit_quaternion()
        y = random_unit_quaternion()
        s += np.linalg.norm(mult(x, y) - mult(y, x))
    
    print(s/N)

In this code x and y have unit length, and so xy and yx also have unit length. Geometrically, x, y, xy, and yx are points on the unit sphere in four dimensions.

When I ran the simulation above, I got a result of 1.13, meaning that on average xy and yx are further from each other than they are from the origin.

To see more than the average, here’s a histogram of ||xy – yx|| with N above increased to 100,000.

histogram

I imagine you could work out the distribution exactly, though it was quicker and easier to write a simulation. We know the distribution lives on the interval [0, 2] because xy and yx are points on the unit sphere. Looks like the distribution is skewed toward its maximum value, and so xy and yz are more likely to be nearly antipodal than nearly equal.

Update: Greg Egan worked out the exact mean and distribution.

Random walk on quaternions

Posted on by John

The previous post was a riff on a tweet asking what you’d get if you extracted all the i‘s, j‘s, and k‘s from Finnegans Wake and multiplied them as quaternions. This post is a probabilistic variation on the previous one.

If you randomly select a piece of English prose, extract the i‘s, j‘s, and k‘s, and multiply them together as quaternions, what are you likely to get?

The probability that a letter in this sequence is an i is about 91.5%. There’s a 6.5% chance it’s a k, and a 2% chance it’s a j. (Derived from here.) We’ll assume the probabilities of each letter appearing next are independent.

You could think of the process multiplying all the i‘s, j‘s, and k‘s together as a random walk on the unit quaternions, an example of a Markov chain. Start at 1. At each step, multiply your current state by i with probability 0.915, by j with probability 0.02, and by k with probability 0.065.

After the first step, you’re most likely at i. You could be at j or k, but nowhere else. After the second step, you’re most likely at -1, though you could be anywhere except at 1. For the first several steps you’re much more likely to be at some places than others. But after 50 steps, you’re about equally likely to be at any of the eight possible values.

Related post: How far are quaternions from being commutative?

Wolfram Alpha, Finnegans Wake, and Quaternions

Posted on by John

James Joyce

I stumbled on a Twitter account yesterday called Wolfram|Alpha Can’t. It posts bizarre queries that Wolfram Alpha can’t answer. Here’s one that caught my eye.

Suppose you did extract all the i‘s, j‘s, and k‘s from James Joyce’s novel Finnegans Wake. How would you answer the question above?

You could initialize an accumulator to 1 and then march through the list, updating the accumulator by multiplying it by the next element. But is there a more efficient way?

Quaternion multiplication is not commutative, i.e. the order in which you multiply things matters. So it would not be enough to have a count of how many times each letter appears. Is there any sort of useful summary of the data short of carrying out the whole multiplication? In other words, could you scan the list while doing something other than quaternion multiplication, something faster to compute? Something analogous to sufficient statistics.

We’re carrying out multiplications in the group Q of unit quaternions, a group with eight elements: ±1, ±i, ±j, ±k. But the input to the question about Finnegans Wake only involves three of these elements. Could that be exploited for some slight efficiency?

How would you best implement quaternion multiplication? Of course the answer depends on your environment and what you mean by “best.”

Note that we don’t actually need to implement quaternion multiplication in general, though that would be sufficient. All we really need is multiplication in the group Q.

You could implement multiplication by a table lookup. You could use an 8 × 3 table; the left side of our multiplication could be anything in Q, but the right side can only be i, j, or k. You could represent quaternions as a list of four numbers—coefficients of 1, i, j, and k—and write rules for multiplying these. You could also represent quaternions as real 4 × 4 matrices or as complex 2 × 2 matrices.

If you have an interesting solution, please share it in a comment below. It could be interesting by any one of several criteria: fast, short, cryptic, amusing, etc.

Update: See follow up post, Random walk on quaternions

More quaternion posts

Mathematical modeling in Milton

Posted on by John

In Book VIII of Paradise Lost, the angel Raphael tells Adam what difficulties men will have with astronomy:

Hereafter, when they come to model heaven
And calculate the stars: how they will wield the
The mighty frame, how build, unbuild, contrive
To save appearances, how gird the sphere
With centric and eccentric scribbled o’er,
Cycle and epicycle, orb in orb.

 

Related post Quaternions in Paradise Lost

Quaternions in Paradise Lost

Posted on by John

Last night I checked a few books out from a library. One was Milton’s Paradise Lost and another was Kuipers’ Quaternions and Rotation Sequences. I didn’t expect any connection between these two books, but there is one.

photo of books mentioned here

The following lines from Book V of Paradise Lost, starting at line 180, are quoted in Kuipers’ book:

Air and ye elements, the eldest birth
Of nature’s womb, that in quaternion run
Perpetual circle, multiform, and mix
And nourish all things, let your ceaseless change
Vary to our great maker still new praise.

When I see quaternion I naturally think of Hamilton’s extension of the complex numbers, discovered in 1843. Paradise Lost, however, was published in 1667.

Milton uses quaternion to refer to the four elements of antiquity: air, earth, water, and fire. The last three are “the eldest birth of nature’s womb” because they are mentioned in Genesis before air is mentioned.

 

Dot, cross, and quaternion products

Posted on by John

This post will show that

quaternion product = cross product – dot product.

First, I’ll explain what quaternions are, then I’ll explain what the equation above means.

The complex numbers are formed by adding to the real numbers a special symbol i with the rule that i2 = -1. The quaternions are similarly formed by adding to the real numbers i, j, and k with the requirement [1] that

i2 = j2 = k2 = ijk = -1.

A quaternion is a formal sum of a real number and real multiples of the symbols i, j, and k. For example,

q = w + xi + yj + zk.

In this example we say w is the real part of q and xi + yj + zk is the vector part of q, analogous to the real and imaginary parts of a complex number.

The quaternion product of two vectors (x, y, z) and (x´, y ´, z´) is the product of q = xi + yj + zk and q‘ = x’i + y’j + z’k as quaternions. The quaternion product qq´ works out to be

– (xx´ + yy´ + zz´) + (yz´ – zy´)i +(zx´ – xz´)j + (xy´ – yx´)k

The real part is the negative of the dot product of (x, y, z) and (x´, y´, z´) and the vector part is the cross product of (x, y, z) and (x´, y´, z´).

NB: The context here is vectors of length 3 embedded in the quaternions. In general the quaternion product is more complicated. The products are simpler in the special case of the real component being zero. See, for example, this post.

This relationship is an interesting bit of algebra on its own, but it is also historically important. In the 19th century, a debate raged regarding whether quaternions or vectors were the best way to represent things such as electric and magnetic fields. The identity given here shows how the two approaches are related.

Related posts

[1] To multiply two quaternions, you need to know how to multiply i, j, and k by each other. It is not immediately obvious, but you can derive everything from i2 = j2 = k2 =ijk = -1. For example, start with ijk = -1 and multiply both sides on the right by k. So ijk2 = –k, and since k2 = -1, ij = k. Similar manipulations show jk = i and ki = j.

Next, (jk)(ki) = ij, but it also equals jk2i = –ji, so ij = –ji = k. Similarly kj = –jk = –i and ik = –ki = –j and this completes the multiplication table for i, j, and k.

The way to remember these products is to imagine a cycle: i -> j -> k -> i. The product two consecutive symbols is the next symbol in the cycle. And when you traverse the cycle backward, you change the sign.